1.复数的几种表示形式

一个复数有多种表示形式。复数F的代数形式为

式中，——虚单位；

a——复数F的实部；

b——复数F的虚部。取复数的实部和虚部分别用下列符号表示：

Re[F]=a， lm[F]=b

一个复数F在复平面（Complex Plane）上可以用一条有向线段表示，如图5-2所示。

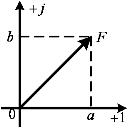
复数F的三角形式为

式中，——复数的模；

φ——复数的复角，可以用弧度或度表示。

、φ、a和b之间的关系为

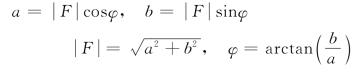
根据欧拉公式ejθ=cosθ+jsinθ，可得

复数的指数形式为

复数的极坐标形式为(www.daowen.com)

F*表示复数F的共轭复数（Conjugate Complex），即对于复数F=a+jb，其共轭复数F*为

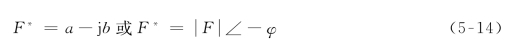
2.复数四则运算

复数的相加和相减运算用代数形式进行，例如，设两复数为F1=a1+jb1，F2=a2+jb2，则

这就是说，两复数相加、减对应于两复数的实部相加、减和虚部相加、减。

若两复数相等，则对应的两复数的实部相等，虚部相等。

复数的相加减运算也可按平行四边形法则在复平面上用矢量的相加减求得，如图5-3所示。

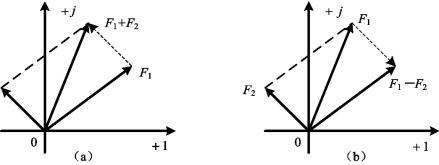
图5-3　复数的加法与减法运算

（a）F1+F2；（b）F1-F2

复数相乘和相除运算用指数形式或极坐标形式比较方便，例如，设两复数为

则

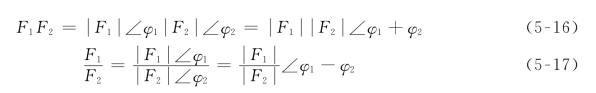
这就是说两复数相乘时，其模等于两复数模的积，其幅角等于两复数幅角的和；两复数相除时，其模等于两复数模相除，其幅角等于两复数幅角相减。

ejφ=1∠φ是一个模等于1，幅角为φ的复数。任意复数乘以ejφ=1∠φ等于把复数逆时针旋转一个角度φ，而复数的模不变，所以ejφ=1∠φ称为旋转因子（Rotated Factor），即若，则。

根据欧拉公式，可得，，，因此±j和-1都可以看成是旋转因子。