量值和（或）方向随时间变化的量称为时变量，其中随时间作周期性变化的时变量称为周期量，而在一个周期内平均值为零的周期量，称为交流量，如交流电压和交流电流。随时间按正弦规律变化即具有正弦函数形式或余弦函数形式的量统称为正弦量（Sinusoid）。对正弦量的描述可以采用sine函数，也可以采用cosine函数。本书采用cosine函数来表示正弦量。

一般说来，正弦电压u（t）可以表示为

式中，Um、ω和φ分别为正弦电压的振幅（Amplitude）、角频率（Angular Frequency）和初相位（Initial Phase），它们能够完全表征正弦电压，称为正弦电压的三要素。正弦量的三要素所表示的意义如下：

正弦量的振幅又称幅值，它是正弦量在整个变化过程中所能达到的最大值，振幅常带有下标m，如电压振幅Um，电流振幅Im。根据式（5-1）可知，当cos（ωt+φ）=1时，有umax=Um，为正弦量的极大值；当cos（ωt+φ）=-1时，有umax=-Um，为正弦量的极小值。umaxumin=2Um称为正弦量的峰—峰值。

式（5-1）中的（ωt+φ）代表正弦量随时间t变化的角度，反映正弦量变化的进程，称为正弦电压量的相位角，简称相位，单位为弧度（rad）或度（°）。其中，ω称为正弦量的角频率，它是正弦量的相位随时间变化的角速度，即表示单位时间变化的弧度数，可以表示为

单位是弧度/秒（rad/s）。

通常正弦量完成一个循环所需要的时间称为周期（Period），记为T，单位为秒（s），将正弦量每秒完成的循环次数称为频率（Frequency），记为f，单位赫兹（Hz）。因此，正弦量的周期T和频率f之间的关系为(www.daowen.com)

不同地区和不同应用场合所使用的交流电频率是不同的。如中国、俄罗斯以及欧洲等国家电力用交流电的频率标准为50Hz，该频率称为工频，美国为60Hz，日本为50Hz或60Hz，两者并用；通信系统所用频率较高，如无线电调幅广播的载波频率为0.15～18MHz，无线电调频广播的载波频率为88～108MHz，广播电视载波频率为30～300MHz以及0.3～3GHz。

φ是正弦量在t=0时刻的相位，称为正弦量的初相位，简称初相，即

初相位的单位用弧度（rad）或度（°）表示，通常在主值范围内取值，即。初相位与计算零点的选择有关，对于任一正弦量，初相位是允许任意指定的，但对同一电路系统中的许多相关的正弦量，只能相对于一个共同的计时零点确定各自的相位。

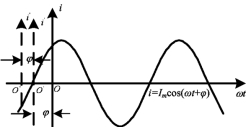
图5-1　正弦量波形及计算起点 与初相位的关系

一般规定将正弦函数表示的正弦量波形由负值变为正值时与横坐标相交且距坐标原点最近的交点称为该波形的起点，即正半周的起点。正弦量初相位的大小即为该正弦波形起点与坐标原点之间的距离。若起点在原点以左，或说当t=0时，正弦量的值大于零，则初相位为正值，即φ＞0，它表示波形的起点超前时间坐标零点的角度为φ；若起点在原点以右，或说当t=0时，正弦量的值小于零，则初相位为负值，即φ＜0，它表示波形的起点滞后时间坐标零点的角度为φ；若起点与原点重合，或说当t=0时，正弦量的值等于零，则初相位为零，即φ=0，它表示波形的起点滞后时间坐标零点的角度为零。图5-1给出了正弦电流波形及计时起点与初相位间的关系。在图5-1中，若取O点为计时起点，正弦波起点在原点左边，所以初相φ＞0；若取O′点为计时起点，正弦波起点在原点处，则初相φ=0；若取O″点为计时起点，正弦波起点在原点的右边，则初相φ＜0。

正弦量有一个十分重要的性质，就是正弦量乘以常数，正弦量的微分、积分，同频率正弦量的代数和等运算，其结果仍为一个同频率的正弦量。