电路在冲激激励作用下的零状态响应称为冲激响应。零状态的一阶电路在冲激激励下的响应为一阶电路的冲激响应;零状态的二阶电路在冲激激励下的响应为二阶电路的冲激响应。图4-48(a)为一个冲激电流激励下的RC并联电路。
当t<0时,电流源Kδ(t)=0,电流源开路,电路处于零状态,即u(0-)=0;
在0-<t<0+这一瞬间,冲激电流源对电容充电,电容储存能量,此时电容电压uC(0+)≠0;因此,当电路中存在冲激电源时,换路定则不再适用;
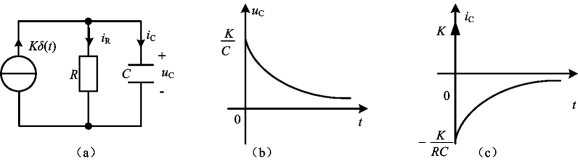
图4-48 RC一阶电路的冲激响应
当t>0之后,电流源Kδ(t)=0,此时电流源又相当于开路,电容通过电阻放电,此时电路中的响应相当于零输入响应。
当t=0时,根据KCL,电路的电流方程为

对式(4-107)两边同时积分可得

式(4-108)中![]() 相加等于一个冲激函数,如果uC为冲激函数,即
相加等于一个冲激函数,如果uC为冲激函数,即![]() 为冲激函数,则
为冲激函数,则![]() 为冲激函数的导数,这样显然不能和方程的右边相等。也就是说
为冲激函数的导数,这样显然不能和方程的右边相等。也就是说![]() 不是冲激函数,只能为有限值。所以左方第二个积分为零。uC跃变,则
不是冲激函数,只能为有限值。所以左方第二个积分为零。uC跃变,则![]() 为冲激函数,所以式(4-108)变为
为冲激函数,所以式(4-108)变为
C[uC(0+)-uC(0-)]=K
因u(0-)=0,可解得
![]()
当t>0之后,激励值为零,从0+开始,电路的响应相当于在初始值下的零输入响应,故
![]()
式(4-110)中τ=RC。将式(4-109)代入式(4-110),得积分常数为
![]()
则电容电压为

电容电压波形如图4-49(b)所示,从图中可以看出电容电压在t=0处有跃变,所以,式(4-111)中的ε(t)不仅有起始作用,还表示此处有跃变,即电容电压从0跃变到![]() 。
。
电容电流为
![]()
其波形如图4-48(c)所示。
同理,图4-49(a)所示为一个冲激电压源作用于RL串联电路,当t<0时,电压源Kδ(t)=0,电压源相当于短路,电路处于零状态,即iL(0-)=0;在0-<t<0+瞬间,冲激电压源在瞬间完成对电感的充磁,电感电流突然增大,电感储存能量,此时电感电流iL(0+)≠0;当t>0之后,电压源Kδ(t)=0,此时电压源又相当于短路,电感通过电阻释放能量,此时电路的响应相当于零输入响应。
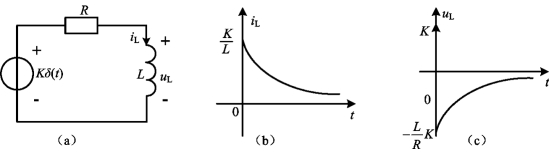
图4-49 RL一阶电路的冲激响应
当t=0时,根据KCL,电路的电流方程为
![]()
对式(4-113)两边同时积分可得
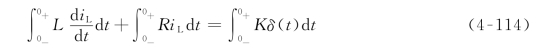
显然,在式(4-114)中,RiL只能是有限值,而![]() 则是冲激函数,因此,式(4-114)中的第二项积分为零,所以有
则是冲激函数,因此,式(4-114)中的第二项积分为零,所以有
L[iL(0+)-iL(0-)]=K
利用iL(0-)=0,从而可得

当t>0之后,激励值为零,从0+开始,电路的响应相当于在初始值下的零输入响应,故
![]()
式(4-116)中![]() 。将式(4-115)代入式(4-116),得积分常数为
。将式(4-115)代入式(4-116),得积分常数为
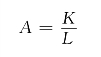
则电感电流为

电感电压为
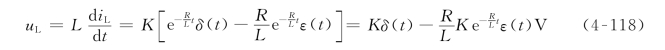
由式(4-117)和式(4-118)可给出电感电流和电感电压波形分别如图4-49(b)和图4-49(c)所示。在t=0瞬间,冲激电压源Kδ(t)全部加在电感两端,使电感电流发生跃变。随后电源相当于短路,电感通过电阻释放能量,电感电压降低,放电电流逐渐减小,直至为零。
由此可见,当动态电路中加入冲激激励时,电容上可能会有冲激电流,电感两端可能会有冲激电压,因而导致电感电流和电容电压的跃变,此时,换路定则不再适用。
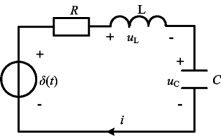
图4-50 RLC二阶电路的冲激响应
零状态的二阶电路在冲激激励下的响应就是二阶电路的冲激响应。图4-50是一个零状态的RLC串联电路,在t=0时冲激电压源δ(t)接通。
若以uC为变量,根据KVL可得电路方程
![]()
由于δ(t)在t≠0时为零,而在t=0时电路受到冲激电压激励而获得了一定能量,在t≥0+时放电,即在t≥0+时,有
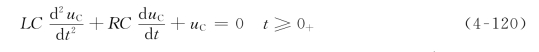
要解方程式(4-120),关键得求出初始能量对应的初始条件uC(0+)和![]() 。为此把式(4-119)在0-至0+时间间隔内积分,得
。为此把式(4-119)在0-至0+时间间隔内积分,得
![]()
由于为零状态,所以有uC(0-)=0,iL(0-)=0,故有![]()
![]() 。由于uC不可能是阶跃函数或冲激函数,否则式(4-119)不能成立,就是说uC不可能跃变。仅
。由于uC不可能是阶跃函数或冲激函数,否则式(4-119)不能成立,就是说uC不可能跃变。仅![]() 才能发生跃变。这样有
才能发生跃变。这样有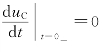 ,uC(0+)=uC(0-)=0,所以有
,uC(0+)=uC(0-)=0,所以有
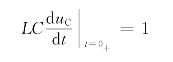
即
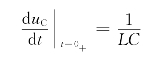
该式说明,冲激电压源在0-至0+时间间隔内使电感电流跃变,跃变后![]()
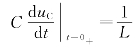 ,电感中储存一定的磁场能量,而冲激响应就是由此磁场能量引起的变化过程。
,电感中储存一定的磁场能量,而冲激响应就是由此磁场能量引起的变化过程。
在t≥0+时为零输入解,其过程和二阶电路零输入响应相同,即
![]()
由初始条件有

联立求解得
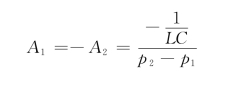
所以,电容电压为
![]()
根据单位冲激函数δ(t)和单位阶跃函数ε(t),可以得出同一电路中阶跃响应与冲激响应的关系。以一阶电路为例,设所加激励为x(t),产生的响应为y(t),电路的微分方程为
![]()
若施加激励为x(t)=ε(t),其对应的阶跃响应为s(t),则电路的微分方程可以写成
![]()
对于同一电路,若施加的激励为x(t)=δ(t),对应一阶电路的冲激响应为h(t),则电路的微分方程可以写成
![]()
对式(4-122)两边进行求导,并利用单位冲激函数δ(t)和单位阶跃函数ε(t),则有
![]()
比较式(4-123)和式(4-124),可以看出,对于同一电路,电路的阶跃响应s(t)和冲激响应h(t)的关系为(https://www.daowen.com)

式(4-125)和式(4-126)表明,线性电路的单位阶跃响应s(t)对时间的导数就是该电路对应的单位冲激响应h(t)。反之,线性电路的单位冲激响应h(t)对时间的积分就是该电路的单位阶跃响应s(t)。利用这一关系,可以先计算同一电路在阶跃激励下的单位阶跃响应s(t),然后对阶跃响应求导而得到其单位冲激响应h(t)。因此,电路的冲激响应可以有两种计算方法,一种是通过直接分析其过渡过程来进行求解,另一种是利用冲激响应与阶跃响应的关系求解。
例4-29 电路如图4-51(a)所示,求下列三种情况下的响应uC(t)。
(1)iS=δ(t)A,uC(0-)=0;
(2)iS=δ(t)A,uC(0-)=1V;
(3)iS=3δ(t-2)A,uC(0-)=2V
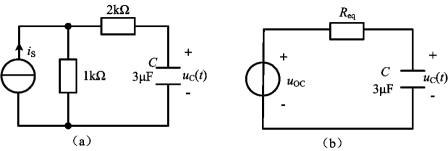
图4-51 例4-29
解 图4-51(a)所示电路的戴维南等效电路如图4-51(b)所示。其中
uoc=1×103iS, Req=(1+2)kΩ=3×103Ω
电路的单位阶跃响应为
![]()
(1)当iS=δ(t)A,uC(0-)=0时,电路的冲激响应为
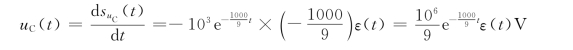
(2)当iS=δ(t)A,uC(0-)=1V时,电路的响应看做是冲激响应与零输入响应之和,即
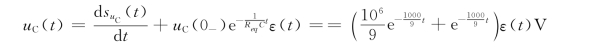
(3)当iS=3δ(t-2)A,uC(0-)=2V时,电路的响应看做是延迟的冲激响应与零输入响应之和,即
![]()
例4-30 求图4-52(a)所示电路中零状态响应iL。
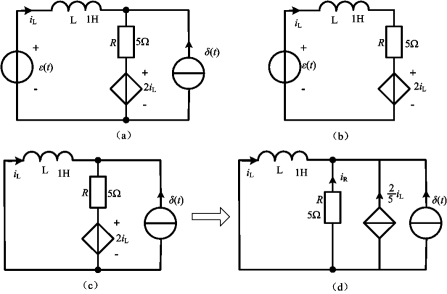
图4-52 例4-30
解 当电路为ε(t)和δ(t)多个激励源共同作用时,可根据线性电路的叠加性质,分别求出ε(t)和δ(t)单独作用时的零状态响应,然后进行叠加。
(1)求单位阶跃响应。令δ(t)不作用,可得图4-52(b),由该图可得
uR+uL+2iL=ε(t)
即
![]()
解得
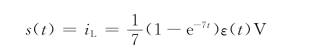
(2)求单位冲激响应。令ε(t)不作用,可得图4-53(c),由该图可得
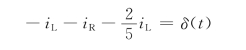
即
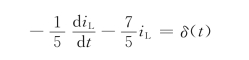
对上式两边积分得
![]()
再利用iL(0-)=0,可求得iL(0+)=-5
t≥0+时的方程为
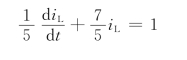
进而可求得
h(t)=iL=-5e-7tε(t)A
所以,电路零状态响应为
![]()
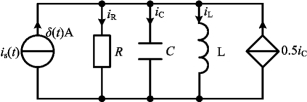
图4-53 例4-31图
例4-31 图4-53所示电路中,已知uC(0-)=0,iL(0-)=0,R=0.2Ω,L=0.25H,C=2F,iS(t)=δ(t)A,试求单位冲激响应iL(t)。
解 方法一:根据KVL和KCL及元件的伏安关系列出微分方程,直接求解微分方程。
对电路应用KCL列节点方程有
iR+iL+iC-0.5iC=iS
将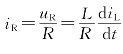 ,
,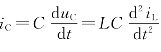 ,iS(t)=δ(t)A代入上式。并代入已知参数整理得
,iS(t)=δ(t)A代入上式。并代入已知参数整理得
![]()
已知uC(0-)=0,iL(0-)=0,在t=0时电路受冲激电流源作用而获得了能量,为求出与初始能量对应的初始条件uC(0+),iL(0+),把上式从t=0-到t=0+区间积分有
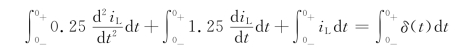
由于iL不可能是阶跃函数或冲激函数,否则电路方程不成立,所以iL不可能跃变,仅![]() 才可能跃变,于是有
才可能跃变,于是有
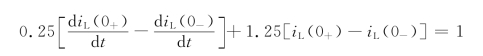
而iL(0+)=iL(0-)=0,![]()
所以
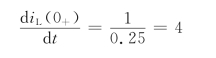
上式说明冲激电流源在t=0-到t=0+区间使电容电压发生了跃变,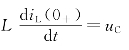
![]() 。t≥0后为零输入响应
。t≥0后为零输入响应
![]()
对应微分方程的特征方程为
p2+5p+4=0
解得特征根
p1=-1, p=-4
代入已知初始条件值有
A1+A2=0 -A1-4A2=4
解得
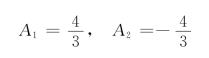
因此,冲激响应
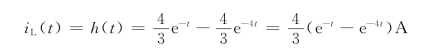
方法二:利用阶跃响应和冲激响应的关系,即![]() 求解。
求解。
根据例4-28所求得的单位阶跃响应
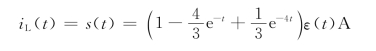
可求得冲激响应为
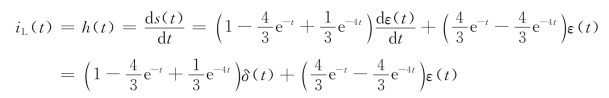
由于在t≥0+时δ(t)=0,上式中的第一项为零,所以冲激响应在t≥0+时
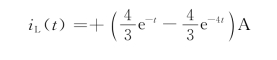
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






