单位冲激函数是一种奇异函数，又称为狄拉克（Dirac）δ函数，可定义为

单位冲激函数δ（t）可以看成是单位脉冲函数的极限情况。图4-46（a）为一个单位矩形脉冲函数pΔ（t）的波形。它的高为，宽为Δ，在保持矩形面积不变的情况下，它的宽度将随着高度的增加而减小。当宽度Δ→0时，脉冲高度，在此极限情况下，可得到一个宽度为零，幅度趋于无限大的面积仍为1的脉冲，这就是单位冲激函数δ（t），可记为

单位冲激函数δ（t）的波形如图4-46（b）所示，有时在箭头旁边注明“1”。强度为K的冲激函数可用图4-46（c）表示，此时在箭头旁边注明“K”。

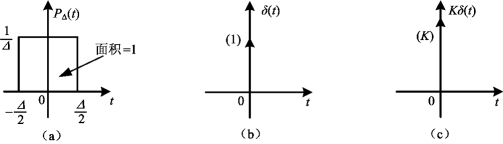
图4-46　脉冲函数和冲激函数

（a）面积为1的脉冲函数；（b）单位冲激函数波形；（c）冲激函数波形

冲激函数的强度是它所包含的面积。因此冲激函数是用它的冲激强度表征的，而不是用幅值来表示，冲激函数在发生冲激时的幅值是无限大的。以单位冲激电压为例，冲激强度的单位是伏特·秒，即Wb。单位冲激电压是指它的强度为1个单位，即1Wb，而不是1V，冲激电压的幅值为无限大。同理，单位冲激电流的强度为1个单位，即1安培·秒或1C，而不是1A。

如果单位冲激量出现的时间不是0而是t0，称它为单位延时冲激函数，写成δ（t-t0）。单位延时冲激函数的定义为

定义式（4-105）表明，在t=t0时刻出现单位面积的冲激，其冲激强度为1个单位。其余任何时刻出现的冲激强度值均为零。单位延时冲激函数的波形如图4-47（a）所示。如果单位延时冲激函数δ（t）的冲激强度不是1而是一个任意常数K，则称为延时冲激函数Kδ（tt0），其波形如图4-47（b）所示。

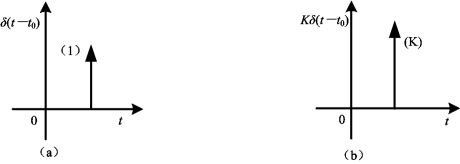
图4-47　单位延时冲激函数和延时冲激函数(www.daowen.com)

（a）单位延时冲激函数波形；（b）延时冲激函数波形

冲激函数有如下两个主要性质：

（1）单位冲激函数δ（t）对时间的积分等于单位阶跃函数ε（t），即

反之，单位阶跃函数ε（t）对时间的一阶导数等于单位冲激函数δ（t），即

（2）冲激函数能把冲激时刻函数f（t）的值筛选出来。

由于当t≠0时，δ（t）=0，所以对任意在t=0时连续的函数f（t），将有

f（t）δ（t）=f（0）δ（t）

将此式两边进行积分，则有

结果为函数在t=0时刻的值f（0）。同理，f（t）与δ（t-t0）的乘积并积分可得

这就说明，冲激函数能把一个函数在某一时刻的值筛选出来，这种性质称为冲激函数的“筛分”性质，又称为取样性质。