单位阶跃函数（UnitStepFunction）ε（t）的定义为

其波形如图4-38（a）所示。当t＜0时，ε（t）=0；当t＞0时，ε（t）=1；当t=0时，ε（t）从0跃变到1。当跃变量不是一个单位，而是k个单位时，可以用阶跃函数kε（t）来表示，即

其波形如图4-38（b）所示。当t＜0时，ε（t）=0；当t＞0时，kε（t）=k；当t=0时，ε（t）从0跃变到k。

延迟单位阶跃函数ε（t-t0）的定义为

也就是说当跃变不是发生在t=0时刻，而是发生在t=t0时刻，可以用延迟单位阶跃函数ε（t-t0）表示，其波形如图4-38（c）所示。而kε（t-t0）则表示延迟阶跃函数。

显然，函数ε（-t）表示t＜0时，ε（-t）=1，t＞0时，ε（-t）=0，如图4-38（d）所示。

图4-38　阶跃函数

（a）单位阶跃函数ε（t）；（b）阶跃函数kε（t）；（c）延迟单位阶跃函数ε（t-t0）；（d）函数ε（-t）

单位阶跃函数ε（t）在电路中可以模拟开关的动作。当直流电压源或直流电流源通过一个开关的作用施加到某个电路时，有时可以表示为一个阶跃电压或阶跃电流作用于该电路。例如图4-39（a）所示开关电路，就其端口所产生的电压波形u（t）来说，在t＜0时，u（t）=0；在t＞0时，u（t）=US；而在开关转换的时刻，即在t=0时刻，电压u（t）从0跃变到US。这种作用等效于图4-39（b）所示的阶跃电压源USε（t）。图4-39（c）所示开关电路，就其端口所产生的电流波形i（t）来说，在t＜0时，i（t）=0；在t＞0时，i（t）=IS；而在开关转换的时刻，即在t=0时刻，电压i（t）从0跃变到IS。这种作用等效于图4-39（d）所示的阶跃电流源ISε（t）；与此相似，图4-39（e）所示电路等效于图4-39（f）所示阶跃电压源USε（-t）；图4-39（g）所示电路等效于图4-39（h）所示阶跃电流源ISε（-t）；引入阶跃电压源和阶跃电流源，可以省去电路中的开关，使电路的分析研究更加方便。

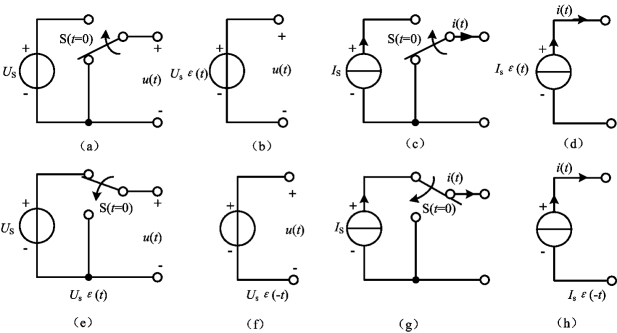
图4-39　用阶跃电源来表示开关的作用

（b）阶跃电压源USε；（d）阶跃电流源ISε（t）；（f）阶跃电压源USε（-t）；（h）阶跃电流源ISε（-t）(www.daowen.com)

阶跃函数具有“起始”一个函数f（t）的作用。将延迟单位阶跃函数乘以f（t）后可以限定函数的定义范围。设f（t）为对所有t都有定义的一个任意函数，则

它的波形如图4-40所示。

图4-40　“起始”一个函数的作用

单位阶跃波形是一种基本波形，可以解析表示其他波形。例如图4-41（a）所示方波电压信号，可以用图4-41（b）所示两个阶跃电压源串联来表示；图4-41（c）所示方波电流信号，可以用图4-41（d）所示两个阶跃电流源并联来表示。

图4-41　用两个阶跃电源表示一个方波信号

例4-25　用阶跃函数表示图4-42所示的方波函数。

图4-42　例4-25图

解　对于图4-42（a）所示的方波，有

f（t）=2ε（t-1）-ε（t-3）-ε（t-4）

对于图4-42（b）所示的方波

f（t）=ε（t）+ε（t-1）-ε（t-3）-ε（t-4）

阶跃函数是一种特殊的连续时间函数，它在信号与系统分析以及电路分析中具有重要作用。从物理角度讲，引入单位阶跃函数一是为了解决单位冲激函数（狄拉克Delta函数）的积分；二是系统在输入信号激励下的响应问题中，为了区分信号加入系统前后两个时间点。信号加入系统开始起作用的时点称为“0时刻”后沿，记为0+，t=0+，就是t＞0；输入信号要加而未加入的时点称为0时刻前沿，记为0-，t=0-，就是t＜0。因而物理上一般不介入（0-，0+）时区，因为这个时区内说不清输入信号到底加入系统了没有，实际上这个时区的宽度也不定，数学上可以认为它趋于0。