二阶电路的初始储能为零，仅由外施加激励源引起的响应称为二阶电路的零状态响应。在如图4-33所示电路中，开关S原来是断开的，且电路已处于稳定状态，电容和电感均无初始储能，即uC（0-）=0，iL（0-）=0。那么该电路中的电容电压uC（t）、回路电流i（t）和电感电压uL（t）在t≥0后随时间的变化规律就是电路在直流激励下的零状态响应。
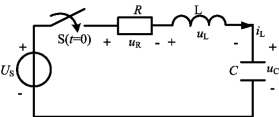
图4-33 零状态的RLC串联电路
在图4-33所示RLC串联电路中，以电容电压uC（t）为待求对象，应用KVL及元件伏安关系，可得在t≥0时，uC（t）满足的微分方程为
令该电容电压的特解即稳态解为u′C=K，代入式（4-96），解得u′C=US
电容电压的暂态解u″C为方程（4-96）对应的齐次方程的通解，即有
所以，方程（4-96）的解为
其中，A1、A2为积分常数，由初始条件决定，其初始条件为
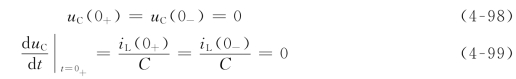
根据上节的讨论，电容电压的暂态解u″C的变化规律根据特征根的不同有三种不同形式，因而与特解u′C合在一起构成的零状态响应也有如下三种情况：
（1）
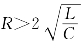，特征根p1、p2是两个不相等的负实根，为非振荡充电过程，电容电压为
（2）
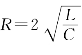，特征根p1、p2是两个相等的负实根，为临界非振荡充电过程，电容电压为
（3）
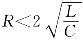，特征根p1、p2是两个不相等的且有负实部的共轭复根，为振荡充电过程，电容电压为
uC（t）=u′C+u″C=US+e-αt（B1cosωt+B2sinωt）=US+Ae-αtsin（ωt+β）
其中的常数由初始条件式（4-98）、式（4-99）决定。
如果电容或电感的初始储能不为零，那么电路的响应就由初始的储能和外加的激励共同决定，这就是电路的全响应，二阶电路的全响应，既可以应用叠加定理求得，也可以通过直接求解二阶微分方程得到。前者由零输入响应和零状态响应之和求得；后者按上一节零状态响应的求解思路一样直接求解微分方程，只不过此时的初始条件不为零。
例4-21 图4-34所示电路，t=0时开关S闭合，求零状态响应uo（t）。
图4-34 例4-21
解 首先建立t＞0时关于待求量uo（t）的微分方程。对节点①、②列KCL方程为
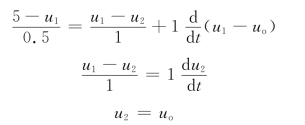
联立求解得
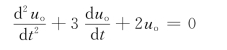
初始条件为
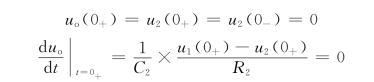
该方程的特征方程为p2+3p+2=0。
得特征根为p1=-1，p2=-2。故得暂态解为
A1e-t+A2e-2t
当t→∞时，电路达到稳定状态，故有uo（∞）=u2（∞）=5V，此即为电路的稳态解。故得零状态解为
uo（t）=5+A1e-t+A2e-2t
应用初始条件有
解得A1=-10，A2=5。
故得
uo（t）=（5-10e-t+5e-2t）V
例4-22 图4-35所示电路，t＜0时开关S打开，且iL（0-）=5A，uC（0-）=2V，令在t=0时刻闭合S，求t＞0时的uC（t）。
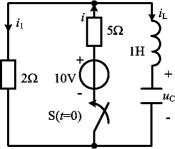
图4-35 例4-22
解 以电容电压uC（t）为待求量，列写微分方程
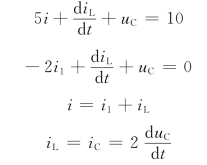
上述4个方程联立求解，得t＞0时电路的微分方程为
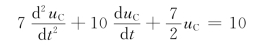
特征方程为
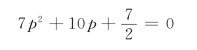
解得特征根为
p1=-0.61， p2=-0.82
故方程的自由解为
u′C=A1e-0.61t+A2e-0.82t
t＞0时电路达到稳定状态时有
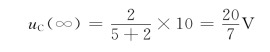
所以，电路的全响应为
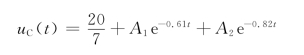
由初始条件
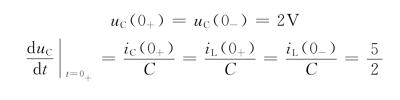
联立求得(www.daowen.com)
A1=8.54， A2=-9.4
故得
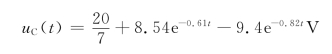
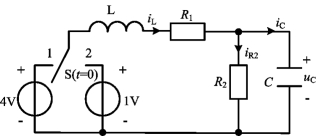
图4-36 例4-23
例4-23 图4-36所示电路中，已知R1=3Ω，R2=1Ω，L=1H，C=1F，开关S原在位置1，电路处于稳态。t=0时开关S由1点转接到2点，试求t≥0时的电流iL。
解 换路前，电路已处于稳态，可求得
iL（0-）=1A， uC（0-）=1V
根据换路定则有
iL（0+）=iL（0-）=1A，
uC（0+）=uC（0-）=1V
根据换路后的电路，依据KVL有
依据KCL有
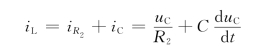
可得
代入参数得
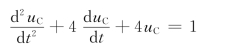
特征方程为
p2+4p+4=0
求得特征根为
p1=p2=-2
由于特征根为两个相等的负实根，所以，对应齐次方程的通解为
uh=（A1+A2t）e-2t
稳态时的响应为
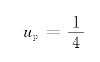
所以，微分方程的全解为
uC（t）=up+uh=（A1+A2t）e-2t
由初始条件
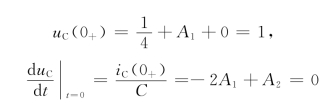
求得待定系数
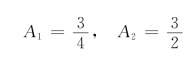
所以，方程的解为
t≥0时的电流iL为
例4-24 图4-37所示电路中，US=50V，R=50Ω，L=0.5H，C=100μF，已知：iL（0-）=2A，uC（0-）=0，求iL，iR。
解 以电感电流iL为未知量，应用节点分析法列方程，得
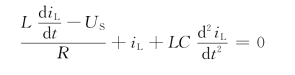
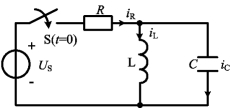
图4-37 例4-24
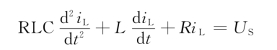
将已知参数代入上式中，得
特征方程为
p2+200p+20000=0
特征根为
p=-100±j100
所以方程的全解为
iL（t）=1+Ae-100tsin（100t+φ）
根据初始条件，可得
iL（0-）=1+Asinφ=2
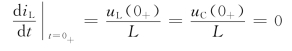
即
100Acosφ-100Asinφ=0
联立求得φ=45°，
。
所以
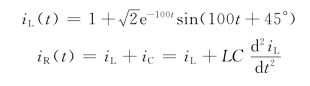
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
