动态电路在换路之前，电路中的储能元件有初始能量，换路后，又外加激励，由激励和原始状态共同引起的响应，称为全响应（Complete Response）。

在图4-21（a）所示的RC电路中，US是一个直流电源，电容原来已充电，其电压为U0。开关S在t=0时闭合。

图4-21　一阶RC电路的全响应

（a）电路；（b）电容电压的变化曲线

当t≥0时，由KVL可得

uC+uR=US

代入元件约束关系得到

初始条件为

方程式（4-47）的特解

u′C=US

对应式（4-47）的齐次方程的通解

因此，方程式（4-47）的通解为

利用初始条件式（4-48），代入式（4-49）中，得

A=U0-US

所以，电容电压全响应为

从式（4-50）可以看出，右边的第一项是电路微分方程的特解，其变化规律与电路施加的激励相同，实质上就是电容电压的稳态分量，所以称为强制分量或稳态分量，而右边的第二项对应的是齐次微分方程的通解，它的变化规律取决于电路的参数而与外施加的激励无关，所以称之为自由分量或暂态分量。因此，响应又可以用强制分量和自由分量来表示，即

电路的全响应=强制分量+自由分量

或

电路的全响应=稳态响应+暂态响应

它反映了电路全响应的层次关系：第一阶段，稳态分量和暂态分量共存，是电路谋求与输入相适应的阶段，稳定的输入要求响应与之相适应，称为过渡过程。由于动态元件的作用，这种状态不是激励一加入就可以一蹴而就，过渡过程的长短，取决于电路的时间常数τ；第二阶段暂态分量消失，电路进入稳态阶段，此后电路的全响应只含稳态响应分量。

若将式（4-50）改写成

不难看出，式（4-51）中右边的第一项是电路的零输入响应，右边的第二项是电路的零状态响应，这说明全响应是零输入响应和零状态响应的叠加，即

电路的全响应=零输入响应+零状态响应

它反映了电路的因果关系，说明电路的全响应分别由初始储能引起的零输入响应和外加激励引起的零状态响应的叠加而成。

以上的分解处理都是从不同角度去分析电路的全响应。结合图4-21（a）所示的RC电路再来看式（4-50）。当开关S闭合前，有uC（0-）=U0，而换路后，由于电容的电压不能跃变，于是有uC（0+）=uC（0-）=U0，也就是说式（4-50）中的U0就是换路后电容电压的初始值。开关S闭合后，经过t→∞时间，有uC（∞）=US为方程的一个特解，对于直流电源激励，也就是电容充电结束后其最终的电压，它等于电源的电压。τ=RC为RC电路的时间常数。因此，电路的全响应是由初始值、特解和时间常数三个基本要素决定的。所以，在直流激励下，就是由初始值uC（0+）、稳态值uC（∞）和时间常数τ三者决定的。因此，RC电路的全响应可写为

式（4-52）表明，在直流激励下，只要算得初始值uC（0+）、稳态值uC（∞）和时间常数τ就可直接写出电容电压的全响应，而不必求解微分方程。

对于图4-22（a）所示的RL电路，以电感电流为求解对象，同理可得到对应的非齐次方程式为

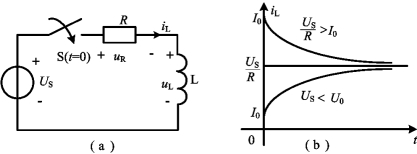
图4-22　一阶RL电路的全响应

（a）电路；（b）电感电流的变化曲线

式（4-53）与RC电路中所得到的式（4-47）形式完全相同，采用类似的求解方法，可得到方程式（4-53）的解为

其中，为RL电路 的时间 常数， 为电路处于稳态时电感中的电流值，I0为电感电流的初始值。所得到的电感电流变化曲线如图4-22（b）所示。

所以，在直流激励下，RL电路中电感电流的全响应是由初始值iL（0+）、稳态值iL（∞）和时间常数τ三者决定的。因此，RL电路的全响应可写为

式（4-55）表明，在直流激励下，只要算得初始值iL（0+）、稳态值iL（∞）和时间常数τ，就可以直接写出电感电流的全响应，而不需要求解微分方程。

在直流激励下，一阶电路中电容的电压和电感的电流全响应我们可以用式（4-52）和式（4-55）直接得到，但直流一阶电路中任一支路中的电压和电流是否也都能表示如式（4-52）和式（4-55）的形式呢？同一电路中的各电压和电流是否也都具有同一时间常数？下面我们来讨论这一问题。

仍以含电容的一阶电路为例。当我们把原电路分为N1，N2两个单口电路，使其中之一单口电路（或网络）N1只含电容，另一单口电路（或网络）N2则包含所有电源和电阻，端口电压即为电容的电压uC（t），它可表示为式（4-52）形式。若以电压为uC（t）的电压源置换电容，则根据置换定理，含源电阻单口电路（或网络）N2内部各电压和电流的解与原电路中该部分中相应的各电压和电流的解答完全相同。设单口电路N2内部任意两节点，如节点j和节点k之间的电压为ujk，并设单口电路N2内部包含有β个直流电流源ISβ和α个直流电压源USα。根据叠加定理，解答ujk可以表示为如下形式

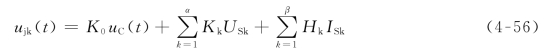
其中，K0、Kk、Hk为取决于电路连接情况及元件参数值的常数。将式（4-52）代入式（4-56）中，可得

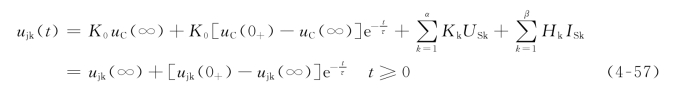
其中

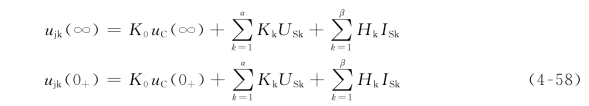
可见，式（4-57）与式（4-52）具有完全相同的形式。因此，在直流一阶RC电路中任何两节点间的电压ujk（t）是按指数规律变化的，且具有与uC（t）相同的时间常数τ。类似的，可以论证，在直流一阶RL电路中任何两节点间的电压ujk（t）或电流ij（t）也是按指数规律变化的，且具有与iL（t）相同的时间常数τ。

因此，对于一个RC电路或RL电路，若用f（t）表示电路中任一支路电流或电压变量，则在直流激励下，若初始值f（0+）、特解稳态值f（∞）和电路的时间常数τ能确定，则全响应可以由下式确定

式中，初始值f（0+）、特解稳态值f（∞）和电路的时间常数τ为求解一阶电路全响应的三要素，这种求解方法称为三要素法（3-factors Method）。

例4-13　图4-23所示电路原已稳定，t=0时，将开关S闭合，试求开关S闭合后的电容电压uC及电容电流iC。

图4-23　例4-13

解　换路前电路已稳定，由图4-23可得uC（0-）=-10V。根据换路定则

uC（0+）=uC（0-）=-10V

t=0时，将开关S闭合。根据换路后的电路可得

时间常数

由三要素法可得(www.daowen.com)

根据电容的伏安关系，可得电容的电流为

例4-14　图4-24（a）所示电路中，其中电路的参数已知，电路达到稳态后，当t=0时开关S由1切换到2，试求换路后的uC。

图4-24　例4-14

解　这是一个含受控源的一阶电路，原则上可以采用时域的经典法或三要素法求解。但若采用三要素法求解，可以回避列写微分方程。对于含受控源的一阶电路，其时间常数可以求出从电容或电感元件两端看进去的电路的戴维南等效电阻，再按相应公式计算。

由图4-24（a）所示电路，换路前

uC（0-）=-8V

由换路定则，可得

uC（0+）=uC（0-）=-8V

由换路后电路有

uC（∞）=4i1+2i1=6×2=12V

等效电阻可由如图4-24（b）所示的等效电路求得，即

u=（4+4）i1+2i1=10i1

所以，等效电阻为

所以时间常数为

τ=ReqC=10×0.1=1s

根据三要素法，换路后电容的电压为

例4-15　图4-25（a）所示电路，t＜0时S打开，电路已达到稳定状态。在t=0时刻闭合开关S，求t＞0时的i（t），并画出i（t）的波形。

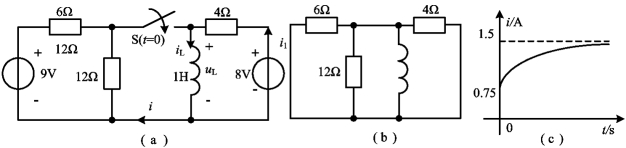
图4-25　例4-15

解　t＜0时S打开，电路已达到稳定状态，故有

t=0时刻S闭合，由换路定则故有

iL（0+）=iL（0-）=2A

t＞0后，有

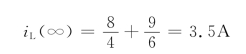
求时间常数的电路如图4-25（b）所示，故有

故得

又

故

故得

i（t）=iL（t）-i1（t）=1.5-0.75e-2t t≥0

其波形如图4-25（c）所示。

例4-16　求图4-26（a）所示电路t＞0时独立电压源的输出功率。

解　在t＞0时的一瞬间，电容电压是确定的，因此可将电容用电压源uC置换，如图4-26（b）所示。图4-26（b）所示电路为电阻电路，由网孔分析，可列图示参考方程下的回路电流方程为

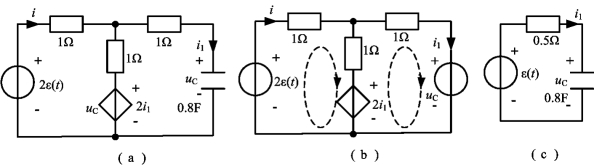
图4-26　例4-16

（1+1）i-1×i1+2i1=2ε（t）

-1×i+（1+1）i1-2i1=-uC

解得

由上式可得电容左端的戴维南等效电路如图4-26（c）所示。

时间常数

τ=RC=0.5×0.8=0.4s

初始值

uC（0+）=uC（0-）=0

稳态值

uC（∞）=uoc=1V

由三要素法可得电容电压为

u（t）=（1-e-2.5t）V

独立电压源的输出功率

p（t）=2ε（t）×i=2（1-e-2.5t）ε（t）W

综上所述，利用三要素法求解一阶电路的基本步骤如下：

（1）确定初始值。用电压为uC（0+）的直流电压源置换电容或用电流为iL（0+）的直流电流源置换电感，所得电路为一直流电阻电路，称为t=0+时的等效电路，由此等效电路可求得任一电压或电流的初始值，即f（0+）。

（2）求稳态值。用开路代替电容或用短路代替电感，所得电路为一直流电阻电路，称为t=∞时的等效电路，由此等效电路可求得任一电压或电流的稳态值，即f（∞）。

（3）求电路的时间常数τ。对于RC一阶电路，τ=ReqC，对于RL一阶电路，其中Req为从电容C或电感L看进去的电路的戴维南等效电阻。

（4）利用公式，代入三要素，整理后获得所求变量响应的时域表达式。