动态电路在没有外加独立电源的情况下，仅由储能元件储存的能量在电路中产生的响应称为零输入响应（Zero-input Response）。零输入响应的过程实质上就是储能元件释放能量的过程。对于一阶电路而言，电路中只含有一个独立的电容或电感，因此，零输入响应是由电容所储存的电场能量或电感所储存的磁场能量所引起的响应。本节讨论RC和RL电路的零输入响应。

1.RC电路的零输入响应

在图4-8（a）所示电路中，开关S闭合前，电容已充电，其电压为U0。在t=0时刻，开关S闭合，此时电容储存的能量将通过电阻以热能的形式释放出来。假设开关S闭合后，电容的电压为uC（t），电阻的电压为uR（t），根据KVL可得

uC（t）-uR（t）=0

由元件的伏安关系，有uR（t）=Ri（t），，代入上式，整理得

式（4-14）为一阶线性齐次微分方程，初始条件为

该方程的解可利用高等数学求微分方程的方法确定，为此，将式（4-14）改写成

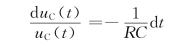
对两边积分得

式中，lnA为积分常量，将该式整理，得

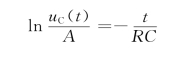
所以，有

由初始条件uC（0+）=U0=A，代入上式，得

电路中电流为

电阻电压为

式（4-16）、式（4-17）、式（4-18）的变化规律如图4-8（b）所示。可见，RC电路中电容电压、电阻电压以及电容电流都按同样的指数衰减规律变化。电容电压在换路瞬间没有跃变，从初始值U0开始按指数规律衰减直到零；电路中电阻电压值在换路瞬间发生了跃变，换路前一时刻为零，换路后其值跃变到U0；同样，电容电流在换路瞬间发生了跃变，从零跃变到。

图4-8　RC电路的零输入响应

从能量的角度来看，RC电路换路前电容储存有电场能量，其电场能量的大小为

换路后，电容与电阻形成了放电回路，电容不断地释放电场能量，电阻不断地将电场能量转换变化为热能而消耗掉，这一过程是不可逆的。在电容放电过程中，电阻消耗的总能量为

正好等于电容储存的电场能量，即电容的储能全部被电阻逐步消耗掉。

从上面讨论可知，RC电路的零输入响应是由于电路的初始储存的能量和它的自身实际特性所产生的，而不是因外部电压源或电流源的影响产生的，所以称为电路的自然响应（Natural Response）。

RC电路中电容的电压、电阻的电压以及电容的电流它们衰减规律快慢取决于指数中的的大小。令τ=RC，其单位为“S”，推导如下

τ具有时间的单位，且仅仅决定于电路元件的参数R和C，与初始状态无关，在有外加激励的电路中，与激励也无关，所以称它为电路的时间常数（Time Constant）。RC电路的时间常数为

将式（4-19）代入式（4-16）得

图4-9　RC电路时间常数的几何意义

令t=τ，电容的电压在此时刻的值为。可见，在时间为τ这一时刻或从换路后一瞬间经过时间τ，电容电压由初始电压值U0衰减到初始值的36.788%，如图4-9所示。也就是说，电容电压由初始值衰减到初始值的36.788%所需要的时间为τ。τ值越大，电压衰减越慢，如图4-9中τ1＞τ，所以τ1所对应的曲线比τ对应的曲线衰减要慢。

由于τ与R、C的乘积成正比，所以可通过改变R、C的参数来调整时间常数，以改变电容放电的快慢。从理论上讲，RC电路的过渡过程需要经历无限长时间才能结束，从而达到新的稳态。将t=τ，2τ，3τ，4τ，5τ分别代入式（4-16）中可得电容的电压分别为0.36788U0、0.13543U0、0.04979U0、0.01832U0和0.00674U0。可见当为t=5τ，此时电容电压几乎接近于零，故认为电容的放电过程已基本结束。因此，在实际中，一般认为动态电路的过渡过程的持续时间为（3～5）τ。

例4-5　电路如图4-10（a）所示，电容原充有24V电压，求开关S闭合后，电容电压和各支路电流随时间变化的规律。

解　这是一个求一阶RC零输入响应问题，t＞0时的等效电路如图4-10（b）所示，因此，有

由题意有

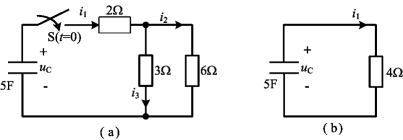
图4-10　例4-5图

U0=24V， R=2+（3∥6）=4Ω

所以，时间常数为

τ=RC=5×4=20s

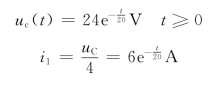
由分流公式，得

例4-6　电路如图4-11（a）所示，求：（1）当开关S闭合后各元件的电压和电流随时间变化的规律，（2）电容的初始储能和最终时刻的储能及电阻的耗能。

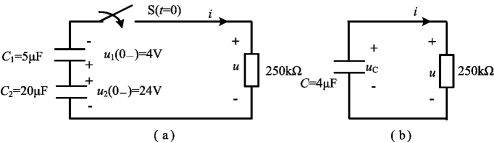
图4-11　例4-6图

解　这是一个求一阶RC零输入响应问题，t＞0时的等效电路如图4-11（b）所示，因此有

uC（0+）=uC（0-）=-4+24=20V，

τ=RC=250×4×10-3=1s

所以有

u（t）=uC（t）=20e-t t≥0

两个电容的电压分别为

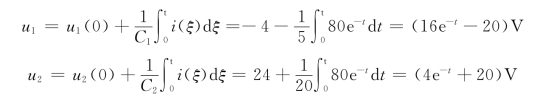
初始储能

最终储能

电阻耗能

4.RL电路的零输入响应

图4-12所示电路为另一种形式的一阶电路，称RL电路。换路前开关S接于触点1，且电路已处于直流稳态。当t=0时，开关S由触点1切换到触点2。

(www.daowen.com)

图4-12　RL一阶电路及零输入响应

由换路前的直流稳态电路可求出电感电流的初始值为

在换路后的电路中，应用KVL，有

将，uR（t）=RiR（t）代入式（4-20），并利用iR（t）=iL（t），有

式（4-21）为一阶线性齐次微分方程，初始条件为

和RC一阶电路的状态方程形式相同，其通解形式为

将式（4-23）代入式（4-21），消除公因子Aept便得到微分方程的特征方程（Characteristic Equation）

Lp+R=0

故特征根（Characteristic Root）为

则所求微分方程的通解为

令，则式（4-24）可以表示为

其中，A为积分常数（Integration Constant），它由电路的初始状态决定，由式（4-22）表示的初始条件可求得A=I0。故电感电流的零输入响应为

电感的电压为

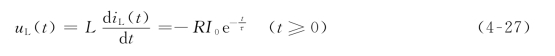
电阻的电压为

根据式（4-26）～式（4-28）绘出电感电流、电感电压和电阻电压的变化规律如图4-12（b）所示。可见，电感电压、电阻电压和电感电流都按相同的指数衰减规律变化。电感电流在换路瞬间没有跃变，从初始值I0开始按指数规律衰减直到零；电路中电阻电压值在换路瞬间发生了跃变，换路前一时刻为零，换路后一时刻其值为RI0；同样，电感电压在换路瞬间发生了跃变，从零跃变到-RI0。

从能量的角度来看，RL电路换路前电感储存有磁场能量，其磁场能量的大小为

换路后，电感与电阻形成了放电回路，电感不断地释放磁场能量，电阻不断地将磁场能量转换变化为热能而消耗掉，这一过程是不可逆的。在电感消磁过程中，电阻消耗的总能量为

正好等于电感储存的磁场能量，即电感的储能全部被电阻逐步消耗掉。

RL电路中电感的电流、电阻的电压以及电感的电压它们衰减规律快慢取决于指数中的τ的大小。，其单位为“S”，推导如下

在实际中，一般认为RL电路的过渡过程的持续时间为（3～5）t。

例4-7　电路如图4-13（a）所示，t=0时，开关S打开，求uV。若电压表的量程为50V，则在开关S打开时会产生什么影响，如何消除影响。

解　这是一个求一阶RL零输入响应问题，在t＜0时，开关S是闭合的，电路达到直流稳态，所以电感相当于短路，所以，有

一阶RL零输入响应为

电路的时间常数为

图4-13　例4-7图

利用初始条件，可得

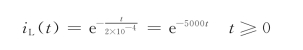
所以，有

uV=-RiL（t）=-10×103×e-5000t t≥0

当开关S断开瞬间，有

uV（0+）=-10×103V

此时，电压已超过了电压表的量程，该电压表会损坏。为保护电压表，可在电压表的两端并接一个二极管来保护电压表，如图4-13（b）所示。

例4-8　电路如图4-14（a）所示，t=0时，开关S由1切换到2，求电感电压和电流及开关两端电压u12。

图4-14　例4-8图

解　这是一个求一阶RL零输入响应问题，在t＜0时，开关S在触点1处，电路处于直流稳态，电压相当于短路，所以，有

由换路定则，t=0，开关S由1切换到2时，有

iL（0+）=iL（0-）=2A

所以，t=0+时，等效电路如图4-14（b）所示，其中

一阶RL零输入响应为

利用初始条件，可得电感电流为

iL=2e-t t≥0

电感电压为

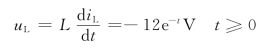
开关S两端电压u12为

综合以上讨论可知：

（1）一阶电路的零输入响应是由储能元件的初始值引起的响应，都是由初始值衰减为零的指数衰减函数。满足以下关系

（2）衰减快慢取决于时间常数τ，对于RC电路有τ=RC，对于RL电路有。其中，R为与动态元件相连的一端口电路的等效电阻。

（3）同一电路中所有响应具有相同的时间常数。

（4）一阶电路的零输入响应和初始值成正比，称为零输入线性。