确定动态电路初始条件的基本步骤：

（1）由换路前电路（稳定状态）求uC（0-）和iL（0-）。

uC（0-）和iL（0-）需要根据t=0-时刻的电路状态进行计算。一般需要作出t=0-时刻的等效电路，然后用电路分析的一般方法来求解。若换路前电路处于直流稳态，即电路中支路电压和电流都是直流量，则电容相当于开路，电感相当于短路，用开路线代替电容，用短路线代替电感，得到的就是t=0-时刻的等效电路，根据此时的电路求uC（0-）和iL（0-）。

（2）根据换路定则或电荷守恒、磁链守恒定律求uC（0+）和iL（0+）。

电容电压的初始值和电感电流的初始值，即电路的初始状态，可由换路定则确定。当电路中电容电压和电感电流无跃变时，有

uC（0+）=uC（0-）， iL（0+）=iL（0-）

（3）画出t=0+时刻的等效电路，根据t=0+时刻的等效电路，选择电路分析方法来确定电路中其他待求电压和电流的初始值。

画t=0+时刻的等效电路时，电容用电压等于uC（0+）的电压源代替，电感用电流等于iL（0+）的电流源代替。此时，电路中已无动态元件，因此，就可以选择前面所介绍的电路分析方法来求解待求电压和电流的初始值。在t=0+时刻的等效电路中，独立电源的数值为其在t=0+时刻的激励值，因此，此时，待求电压和电流的初始值就是由电路的初始状态[uC（0+）和iL（0+）]和独立源在t=0+时刻的激励值共同决定的。

（4）uC（0+）和iL（0+）一阶导数初始值确定。

由于，，因此，uC（0+）和iL（0+）一阶导数值初始可由下面式子确定

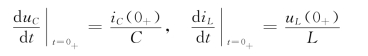
其他待求电压和电流一阶导数的初始值也由t=0+时刻的等效电路来确定。

例4-1　图4-4所示电路，t＜0时，开关S闭合，电路处于稳态，t=0时开关S打开，求iC（0+）。

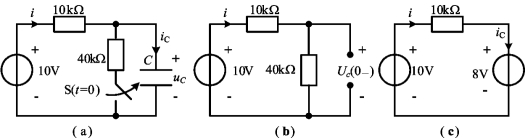
图4-4　例4-1图

（a）电路图；（b）t=0-时等效电路；（c）t=0+时等效电路

解　（1）由t=0-时的电路求uC（0-）

由于当t＜0时，开关S闭合，电路处于稳态，电容相当于开路，如图4-4（b）所示，有

（2）由换路定则求uC（0+）

由于电容上的电压不能跃变，由换路定则，有

uC（0+）=uC（0-）=8V

（3）由t=0+时的电路求iC（0+）

画出t=0+时的等效电路，如图4-4（c）所示，由图可得

例4-2　电路如图4-5所示，t=0时闭合开关S，求uL（0+）。

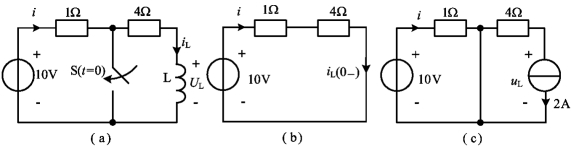
图4-5　例4-2图

（a）电路图；（b）t=0时等效电路；（c）t=0+时等效电路

解 （1）由t=0-时的电路求iL（0-）

由于当t＜0时，开关S打开，电路处于稳态，电感相当于短路，如图4-5（b）所示，有

（2）由换路定则求iL（0+）

由于流过电感的电流不能跃变，由换路定则，有

iL（0+）=iL（0-）=2A

（3）由t=0+时的电路求uL（0+）

画出t=0+时的等效电路，t=0时开关S闭合，而电感由2A的电流源代替，如图4-5（c）所示，由图可得

uL（0+）=-2×4=-8V

例4-3　电路如图4-6（a）所示，已知t＜0时，开关S打开，电路处于稳态，在t=0时刻闭合S，求i（0+），iC（0+），uL（0+），。

图4-6　例4-3图

解　因为t＜0时，开关S打开，电路处于稳态，各电感相当短路，各电容相当开路，所以可得到t=0-的等效电路如图4-6（b）所示，由图得

uC（0-）=1×i2（0-）=1×2=2V

由于i1即为1H电感的电流，i2即为2H电感的电流，所以换路后i1、i2和uC的初始值可由换路定则求得，其他变量的初始值由t=0+的等效电路（如图4-6（c）所示）求得，有

i1（0+）=i1（0-）=2A， i2（0+）=i2（0-）=2A， uC（0+）=uC（0-）=2V

uL（0+）=-1×i2（0+）=-1×2=-2V

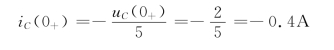
又因有(www.daowen.com)

i1（0+）=iC（0+）+i2（0+）+i（0+）

故得

i（0+）=i1（0+）-iC（0+）-i2（0+）=2-（-0.4）-2=0.4A

又因有

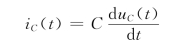
故得

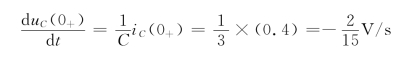
例4-4　电路如图4-7（a）所示，求：（1）iL（0+），uC（0+），uR（0+）；（2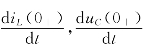），；（3）iL（∞），uC（∞），uR（∞）。

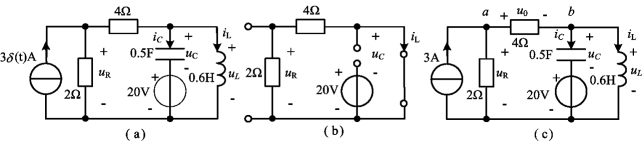
图4-7　例4-4图

解　（1）因为t＜0时，3δ（t）A=0，在t=0-时，电路已达到稳态，所以，电容相当开路，电感相当等效电路，得到如图4-7（b）所示的等效电路，由图可得

iL（0-）=0， uR（0-）=0， uC（0-）=-20V

t＞0时，3δ（t）A=3A，等效电路如图4-7（c）所示。由于电容的电压和电感的电流不能跃变，所以，有

iL（0+）=iL（0-）=0， uC（0+）=uC（0-）=-20V

令4Ω电阻两端电压为u0，对节点a应用KCL，有

对图4-7（c）的中间网孔，应用KVL，有

-uR（0+）+u0（0+）+uC（0+）+20=0

由于uC（0+）=-20V，所以由上式得到

uR（0+）=u0（0+）

所以，有

uR（0+）=u0（0+）=4V

（2）由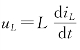，有

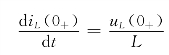
对图4-7（c）中的右网孔，应用KVL，有

uL（0+）=uC（0+）+20=-20+20=0

因此，有

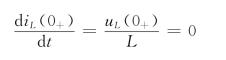
由，有

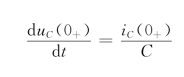
对节点b处应用KCL，有

而于u0（0+）=4V，iL（0+）=0，，所以，有

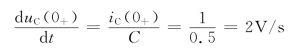
对节点a用KCL，有

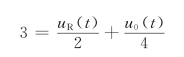
对上式各项求导，并以t=0+，有

再对图4-7（c）的中间网孔，应用KVL，有

-uR（t）+u0（t）+uC（t）+20=0

对上式各项求导，并以t=0+，有

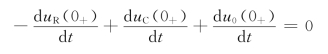
故有

因为uR（t）=5iR（t），所以，有

（3）当t→∞，电路达到稳态，则电路如图4-7（b）所示，但3A电流源要加上，由分流原理可知