对于电阻电路，由于电路中电阻元件的电压和电流的约束关系是代数关系，根据KVL，有uS=uR=RiR，因此，描述电阻电路的数学模型是代数方程。电阻电路中任一时刻的响应仅与此时刻的激励有关，而与激励的过去无关。如图4-1（a）所示电路中，开关S闭合前：iR=0，uR=0，电路处于一种状态；开关S闭合后 ，uR=uS，电路处于另一种状态。这就是说，开关S闭合后，电路从一种工作状态（iR=0，uR=0）直接变化到另一种工作状态（，uR=uS），其间没有过渡过程。这就是说电阻电路只有两个稳定的工作状态而没有过渡状态。

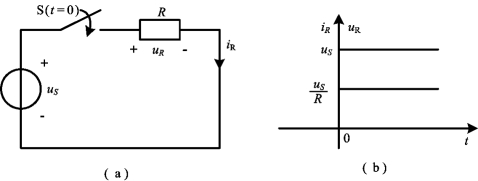
图4-1　电阻电路从一个稳定状态到另一个稳定状态的变化过程

（a）电路图；（b）开关闭合后电流与电压变化曲线

当电路中含有电容元件时，由于电容电压和电流的约束关系是微分关系或积分关系，对于图4-2（a）所示电路，根据KVL，有，所以描述电路的数学模型是以电压为变量的微分方程。由于电容元件的记忆特性，这种电路任一时刻的响应除与此时刻的激励有关外，还与激励的过去有关。如图4-2（a）所示电路中，假设电容开始没有充电，开关S闭合前，电路处于一种稳定状态（iC=0，uC=0），开关S闭合后，电源对电容进行充电，当经过很长时间后，电容充电结束，电路达到另一种稳定状态（iC=0，uC=uS）。在从前一个稳定状态到后一个稳定状态的过程中，由于电容电压不能从零跃变到uS，需要经过一定的过渡过程，即电容电流为有限值，电容上的电压不会跃变。

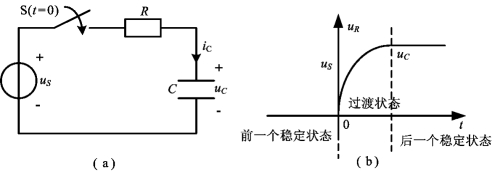
图4-2　RC电路从一个稳定状态到另一个稳定状态的变化过程

（a）电路图；（b）开关闭合后电流与电压变化曲线

若将电路中的电容换成电感，类似有，若电感电压为有限值，则电感电流也不会跃变。这就是说，含有电容或电感的电路中，电容的电压或电感的电流是逐渐变化的，其间存在一个过渡的过程。

把含有动态元件电容或电感的电路称动态电路。动态电路是用微分方程来描述的。当动态电路状态发生改变时需要经历一个变化过程才能达到新的稳定状态。这个变化过程称为电路的过渡过程。动态电路有两种工作状态：稳态和暂态。电路在直流激励的作用下，各条支路的响应都是直流时，电路处于稳定工作状态，称电路处于直流稳态。电路处于直流稳态时，电感上无变化的电流，电感两端的电压为零，相当于短路；电容上无变化的电压，电容支路无电流，相当开路。电路在周期激励的作用下，各支路的响应均为周期函数值时，电路也处于稳态，称电路处于交流稳态。

对于RC电路，电路中只有一个电容元件。如图4-2（a）所示电路，若以电容上的电压为变量，当开关闭合后，利用元件伏安关系和KVL，有

若以电容上的电流为变量，有

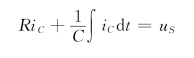
即

对于RL电路，电路中只有一个电感元件。同理，若以电感的电流为变量，有(www.daowen.com)

若以电感中的电压为变量，有

可见，含有一个动态元件电容或电感的线性电路，其电路方程为一阶线性常微分方程（Ordinary Differential Equation），因而这种电路称为一阶电路（First-order Circuits）。

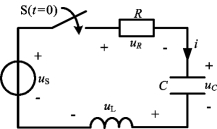
图4-3　RLC电路

对于RLC电路，如图4-3所示，根据KVL和元件的伏安关系，有

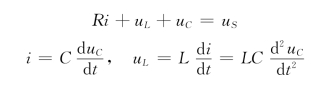
所以

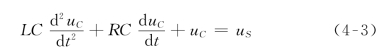
可见，含有两个不同动态元件的线性电路，或者两个独立电容元件或两个独立的电感元件的电路，其电路方程为二阶线性常微分方程，这种电路称为二阶电路（Second-order Circuits）。表明用微分方程来描述动态电路的电路方程，动态电路中独立储能元件的个数即为电路的阶数，亦即描述其微分方程的阶数。一阶电路中只有一个动态元件，描述电路的方程是一阶线性微分方程，其一般形式为

二阶电路中有二个动态元件，描述电路的方程是二阶线性微分方程，其一般形式为

n阶电路中有n个动态元件，描述电路的方程是n阶微分方程，其一般形式为

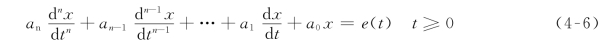
分析和求解动态电路的过渡过程有两种方法：时域分析法（Time Domain Analysis）和复频域分析法（Frequency Domain Analysis）。时域分析法简称时域法，也称经典分析法，即求解微分方程的方法，这时需要确定方程的初始条件。复频域分析法称为拉普拉斯变换法。本章只讨论时域分析法，拉普拉斯变换法将在第12章讨论。