在电路中存在着很多对偶现象，利用这些对偶，可以很方便得到一些关系式或结论，因此，对偶的概念也成为求解电路问题的一个省时而有效的方法。在前面章节的讨论中，我们已发现电路中有些电路元件、电路变量、电路结构、电路定律、电路定理和电路的分析方法都是成对出现的，它们之间有着一种明显的类比关系。例如，欧姆定律的两种表达式，即u=Ri和i=Gu。若把这两式中的电压u和电流i互换，电阻R和电导G互换，则这两个关系式可以彼此转换。电容元件的伏安关系式和电感元件伏安关系式 中，若把电压u和电流i互换，电容C和电感L互换，则这两个关系式也可以彼此转换。像这种类比性质就是对偶性（Duality）。其中，电压u和电流i称之为对偶变量（Dual Variable）；电阻R和电导G、电容C和电感L称之为对偶参数；电阻和电导、电容和电感称之为对偶元件（Dual Element）；u=Ri和i=Gu、和称为对偶关系式。在电路分析中，把这些对偶变量、对偶参数、对偶元件和对偶关系式等统称为对偶元素。电路中最基本的对偶元素是两个电路变量：电压u和电流i，所有其他的对偶元素或对偶关系都源自这两者的对偶性，表3-1列出了部分对偶元素。

表3-1　电路中部分对偶元素

可将对偶性表述为对偶原理，即将电路中某一表述关系（如电路方程、电路结构、电路定律、电路定理等）中的元素（电路变量、电路结构、电路元件和电路参数等）用其相应的对偶元素对应转换后所得到的对偶表述也成立。

对偶原理揭示了所谓对偶电路及其电路关系式之间的内在联系，由此产生了电路的对偶分析方法。由对偶原理可知，若已知一个电路的结构和方程式以及电路的响应特性，则可以确定其对偶电路的结构和方程以及响应特性。因此，可以利用对偶性作为电路分析的工具，这就是对偶分析方法。对偶方法不但为电路的分析与计算提供了新的计算方法，且使得全部电路问题的研究与公式的记忆工作减半。此外，对偶方法也为寻找新的电路开拓了广阔的道路。

这里所说的对偶电路（Dual Circuit），可以从其描述方程和电路构成两个方面定义：用对偶量交换后两个电路的描述方程形式完全相同，即各项系数及激励数值均完全相同仅待求变量不同；两个电路的电路结构对偶，相应的电路元件也对偶且数值相同。

由于电路的对偶性是在其网孔方程与节点方程的基础上得出的，由于非平面电路不能用网孔方程组来描述，因此，对偶性只能用于平面电路，对非平面电路不适用。对于一个给定的平面电路，可以不需要写出其网孔方程或节点方程，而可以按下述三个步骤通过作图的方法求得它的对偶电路。

（1）对给定电路中的每一个网孔，在其中心设置一个节点，作为其对偶电路的非参考节点；在给定的电路之外设置一个节点，作为其对偶电路的参考节点（地）；

（2）把所设定的节点用虚线相互连接构成对偶电路的支路，连接时使每根线只连接一个元件，并以原电路的对偶元件取代该元件；

（3）按如下规则确定电压源的极性和电流源的方向：一个电压源若产生一个正的（顺时针方向）网孔电流，则与之对偶的电流源，其参考方向是由地指向非参考节点的。(www.daowen.com)

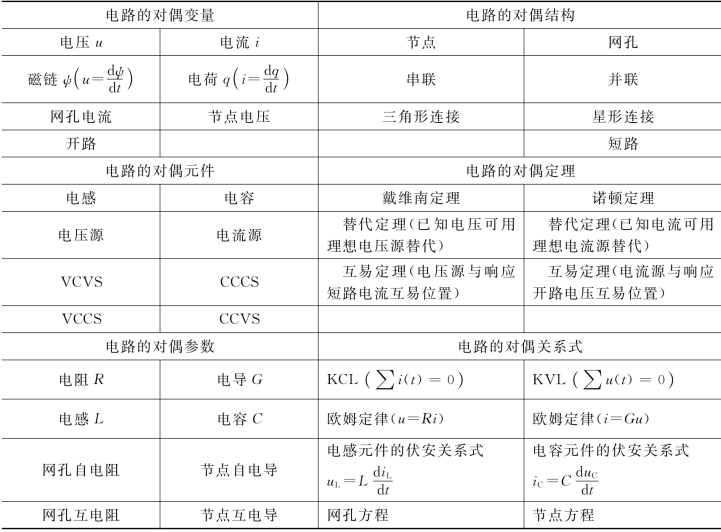
例3-24　画出图3-38（a）所示电路的对偶电路。

图3-38　例3-24图

解　如图3-38（b）所示，首先在两个网孔中心各设置一个节点1和节点2作为非参考节点，而在外面设置节点0作为参考节点，即是对偶电路在地。在每一个节点与经过一个元件的另一个节点间画连线，用对偶元件取代连线所经过的元件，如节点1和节点2间是经过一个2H的电感，则应在该线上放置一个2F的电容；节点2和节点0间的连线经过10mF的电容，则在该线上放置一个10mH的电感；节点1和节点0间有3根连线分别经过6V电压源、2Ω电阻和在t=0闭合的开关K，因此，在它们间的连线上分别放置一个6A的电流源、0.5S的电导和在t=0打开的开关K。由此，可得到图3-38（b）所示电路所对应的对偶电路，如图3-38（c）所示。

例3-25　画出图3-39（a）所示电路的对偶电路。

解　首先在网络外设置一个节点0作参考节点，在每个网孔中心设置节点1，2和3。因为连接节点1和节点0的连线，经过10V的电压源，所以，可用一个10A的电流源取代。由于10V电压源产生一个正的（顺时针方向）网孔电流i1，则与之对偶的10A电流源，其参考方向是由地指向非参考节点1的。连接节点1和节点2的连线经过2F的电容，所以，可用一个2F的电感取代它；同理，连接节点2和节点3的连线经过10Ω的电阻，用一个0.1S的电导取代它；连接节点3和节点0的连线经过3A的电流源，用一个3V的电压源取代它，由于i3=-3A，所以，对应的电压源为u3=-3V。最后得到如图3-39（c）所示的对偶电路。

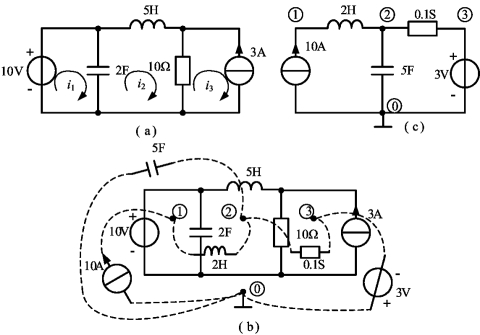
图3-39　例3-25图

应当注意的是，对偶与等效是两个完全不同的概念，即互相对偶的两电路不是相互等效的电路，如RLC串联电路和GCL并联电路互为对偶，但并不等效，等效电路的外特性相同，但两个对偶电路的外特性不一定相同。对于两个等效电路的对偶电路彼此也是等效的。各种对偶关系是相互的，即对任何电路元件或电路进行两次对偶变换，便得到原电路元件或电路。由于功率和能量与电压或电流之间不是一次函数关系，所以功率和能量没有对偶元素。