互易定理（Reciprocity Theorem）反应下述电路特性：对于一个仅含线性电阻且只有一个激励源的二端口电路，当激励和响应互换位置时，将不改变同一激励所产生的响应。由于互换后电路的拓扑结构不变有三种可能，所以，互易定理就有三种特殊形式。

2.互易定理的一般形式

如图3-32所示，N0为线性纯电阻电路（既无独立源，也无受控源），端口1-1′和端口2-2′连接不同的外部条件，则有

图3-32　互易定理的一般形式

现用特勒根定理来证明上述结论。

假设图3-32（a）、（b）所示电路N、为结构相同的线性电阻网络，支路数均为b条，端口1-1′和2-2′分别为支路1和支路2，其余b-2支路都在N内部。设支路1的电流和电压分别为：i1、i2和u1、u2；设支路2的电流和电压分别为和。

根据特勒根定理二有

由于N、内部的b-2支路均为线性电阻，由欧姆定律得

则

所以有

故有

3.互易定理的三种特殊形式

形式一：如图3-33（a）所示电路，N0为只含线性电阻而不含受控源的二端口电路，该电路中只含激励源uS。当电压源uS接在N0的端口1-1′时，在端口2-2′产生的响应为短路电流i2；若将电压源uS移到端口2-2′，并将此时的电压源的电压称为，而在端口1-1′产生的响应为短路电流，如图3-33（b）所示。则有，当时，有。

图3-33　互易定理形式一

由式（3-21）可有

对于图3-31（a），有u1=uS，u2=0；对于图3-33（b），有，，将它们代入上式中便得到

即

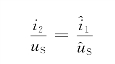
所以，当时，有。

形式二：如图3-34（a）所示电路，N0为只含线性电阻而不含受控源的二端口电路，该电路中只含激励源iS。当电流源iS接在N0的端口1-1′时，端口2-2′开路，其开路电压为u2；若将电流源iS移到端口2-2′，端口1-1′开路，其开路电压为；如图3-34（b）所示。则有，当时，有。

图3-34　互易定理形式二

其证明方法与形式一相同。将i1=-iS，i2=0，，^i代入式（3-21）中，有

即

所以，当时，有。(www.daowen.com)

形式三：如图3-35（a）所示电路，N0为只含线性电阻而不含受控源的二端口电路。当电流源iS接在N0的端口1-1′时，端口2-2′短路，其短路电流i2；图3-35（b）所示电路中，端口2-2′接入电压源uS，端口1-1′开路，其开路电压为，则有，当时，有。

图3-35　互易定理形式三

将i1=-iS，u2=0，代入式（3-21）中有

即

所以，当时，有。

例3-22　如图3-36（a）所示电路中，N为仅由电阻组成的网络。已知u2=6V，求图3-36（b）中u′1。

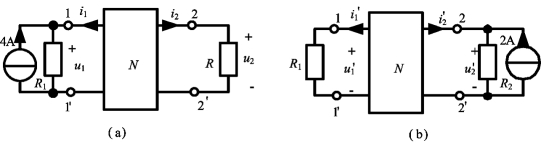
图3-36　例3-22图

解　电路中除电源外，其余部分均由电阻组成的互易网络，根据互易定理，有

解得

例3-23　对图3-37（a）所示电路中的线性电阻网络N进行了两组测试：（1）当uS=9V，iS=0时，N获得功率27W，u2=6V；（2）当uS=0，iS=6A时，N获得功率24W。试求当uS=2V，iS=4A共同激励时，N获得功率。

解　线性电阻网络N获得的功率电压源uS和电流源iS提供的功率，因此，只要求电流i1和电压u2即可求出电压源和电流源的功率。可以利用互易定理、叠加定理和齐次定理来求解。

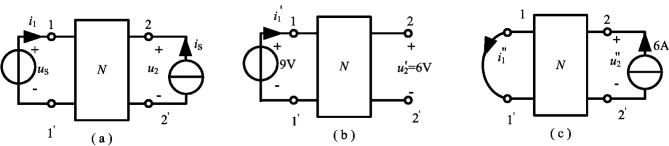
图3-37　例3-23图

（1）根据第一组测试数据，可画出图3-37（b）所示电路。由功率关系有

9i′1=27W

得

i′1=3A

由于当uS=9V时，i′1=3A，u′2=6V；由齐次定理可得，当uS=2V时有

（2）根据第二组测试数据，可画出图3-37（c）所示电路。由功率关系有

6u″2=24W

得

u″2=4V

当iS=9A时，与uS=9V的数值相同，根据互易定理形式三有

i″1=6A

由齐次定理可得，当iS=4A时有

（3）当uS=2V电压源和电流源iS=4A共同作用时，根据叠加定理有

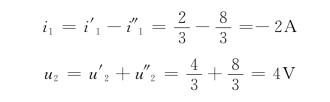
当uS=2V，iS=4A共同激励时，N获得功率为

P=uSi1+u2iS=2×（-2）+4×4=12W