首先讨论图3-12（a）所示电路，设ab两端电压为u，极性如图中所示，从ab处断开将电路分为两部分，则左边电路端口伏安关系为

u=-0.5-2i

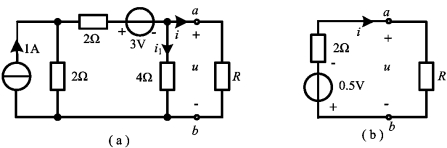
图3-12　等效含源支路

可见图3-12（a）所示电路中ab左边的电路，可以用一个理想电压源和一个电阻的串联来等效，如图3-12（b）所示。这一结果带有普遍性，即任意含源的一端口电路，其端口的电压和电流呈线性关系，可以等效变换为带内阻的电压源，称之为戴维南等效电路（Thewenin's Equivalent Circuit）。

戴维南定理：任一线性含源一端口电路（如图3-13（a）所示），在保持端口电压u和端口电流i的关系完全相同的条件下，可以用一个理想电压源和一个电阻的串联组合来等效置换（如图3-13（b）所示）。其中，此理想电压源的电压为该一端口电路的端口开路电压uoc（如图3-13（c）所示），而电阻为该一端口电路内部所有独立电源为零值时所得的无独立源一端口电路的输入电阻Req（如图3-13（d）所示）。此结论称为戴维南定理，也称为等效电压源定理。

图3-13　戴维南定理

可见，若线性含源一端口电路的端口电压和电流为关联参考方向，则此一端口电路端口的伏安关系可表示为

戴维南定理证明如下：

图3-14（a）中N为任一含源一端口电路，流过任意电路的电流为i，根据替代定理，用一个电流为iS=i的电流源替代任意电路，如图3-14（b）所示。根据叠加定理，当含源一端口电路N内的独立电源单独作用时，外部电流源iS用开路线代替，含源一端口电路N的端口电压为其开路电压uoc，即u′=uoc，如图3-14（c）所示。当外部电流源iS单独作用时，含源一端口电路N内的独立电源均置零，即原一端口电路变成无源一端口电路N0，而无源一端口电路N0可用一个等效电阻Req来代替，如图3-14（d）所示。有u″=-Reqi。所以，含源一端口电路N的端口电压u可表示为

u=u′+u″=uoc-Reqi

图3-14　戴维南定理证明

上述方程对应的电路正好是图3-14（e）所示的戴维南等效电路。这也就证明了戴维南定理。

例3-9　电路如图3-15（a）所示，分别应用电源等效变换和戴维南定理将其化简为最简电路形式。

解　（1）应用电源等效变换求解

将20V电压源和10Ω电阻串联支路变换为一个2A电流源与10Ω电阻的并联，将将10V电压源和10Ω电阻串联支路变换为一个1A电流源与10Ω电阻的并联，两个10Ω电阻并联后得到一个5Ω电阻，如图3-15（b）所示，再将两个并联的电流源合并成一个3A的电流源，然后，再将其变换成一个电压源与一个电阻的串联，如图3-15（c）所示。

图3-15　例3-9图

（2）应用戴维南定理

首先求a、b两端的开路电压uoc。由图3-15（a）所示电路可知

所以有(www.daowen.com)

uoc=10+10i=10+10×0.5=15V

再求等效电阻。将原电路中的独立电源置零，保留其电阻，得到一个由两个10Ω电阻并联的无源一端口电路，其等效电阻为Req=10∥10=5Ω，最后得到等效电路如图3-15（c）所示。可见两种求法的结果一致，但用戴维南定理求解更具普遍性。

例3-10　试说明若含源单口网络开路电压为uoc，短路电流isc，则该含源单口网络戴维南等效电路的串联电阻Req为

解　根据戴维南定理，一个含源一端口电路可等效为一个电压源uoc与一个电阻Req的串联电路，如图3-16（a）所示。因此，原网络N的短路电流isc应等于等效电路的短路电流，而这个等效电路的短路电流显然为 ，如图3-16（b）所示。因此有

图3-16　例3-10图

例3-11　电路如图3-17（a）所示，应用戴维南定理求电路中的电流iL。

解　设ab支路断开后的开路电压为uoc，得到如图3-17（b）所示电路，利用回路法可得

2i′+（i′+8i′）×2=20⇒i′=1A

所以，开路电压有

uoc=2（i′+8i′）=2×9×1=18V

将ab支路短路，设短路电流为isc，得到如图3-17（c）所示电路，利用回路法可得

得短路电流

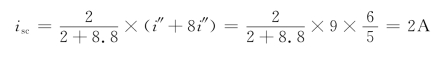
故得输入电阻为

由此，可得戴维南等效电路如图3-17（d）所示，于是得

图3-17　例3-11图

戴维南定理反映用等效电压源置换含源一端口电路后，对外电路没有任何影响，即外电路的电压和电流不会有任何变化，因此，在实际电路分析中应用广泛。但戴维南定理是由叠加定理推导出来的，而叠加定理只适用于线性电路，所以戴维南定理只能适用于线性电路，不适用于非线性电路；而叠加定理应用于含线性受控源电路时，所谓电源单独作用指的是独立电源单独作用，而受控源保持不变，因此应用戴维南定理时，其等效电阻Req是指含源一端口电路N内的独立电源均置零（电压源用短路线代替，电流源用开路代替），受控源保留，而从其端口看所得到的等效电阻；由于一端口电路N要与外电路相连，如果外电路中含有控制量在该一端口电路N中的受控源，则在把一端口电路化简为戴维南等效电路后，受控量所在的支路已被消除，在计算外电路的电流、电压时，无法考虑这一受控源的作用，因此，外电路不能含有控制量在N中的受控源，但控制量可以是端口电压或电流；另外，含源一端口电路N和外电路之间除了他们连接端口之外，应无任何的电或磁的耦合。