在运用支路法、回路法和节点法对复杂电路进行分析时,特别是我们只指对其中某一支路的电压、电流或其中某些局部的电压、电流感兴趣时,我们仍需要解联立方程组来求得所需要的量,这对复杂的电路来说,方程组就嫌太多,而且有些麻烦和不必要。对于这样的问题我们可以这样来处理:将原电路分解为若干个相对简单的子电路或子网络(Subnetwork),对这些子网络逐一求解从而可得到我们所需要的结果。也就是采用分解的方法,把复杂问题简单化处理。
前两章的讨论已知,一个元件的伏安关系是由这个元件本身所确定的,与外接的电路无关。同样,如果一个一端口电路除了通过它的两个端钮与外界相连接外,别无它的联系,那么这个一端口电路的伏安关系也是由一端口电路本身所确定的,与外接电路无关。因此,对于这样的一端口电路我们可以采用分解处理的方法来处理。分解的基本步骤如下:
(1)把给定的电路划分为两个一端口子电路N1和N2;
(2)通过计算或测量方法分别求出子电路N1和N2的伏安关系;
(3)联立两子电路N1和N2的伏安关系式或由它们的伏安关系曲线的交点,求得N1和N2的端口电压和端口电流;
(4)分别求解N1和N2内部各支路电压和电流。
应当说明的是,一般来说子电路的划分是随意的,但在有些情况下,子电路的划分就不是随意了,如我们只对负载的电压、电流、功率感兴趣时;或当N1(N2)的内部情况不明;或N1(N2)是一个不可分割的整体时;或是两个性质不同网络相连接处的电压、电流易于首先求解等,此时,子电路的划分要视方便而定。
下面来讨论分解方法实施问题,为此,先介绍与此密切相关的替代定理或转换定理(Substitution Theorem)。首先,我们来看这样的一个例子:
对图3-8(a)电路应用支路分析法可求得
i1=2A, i2=1A, i3=1A, u3=8V
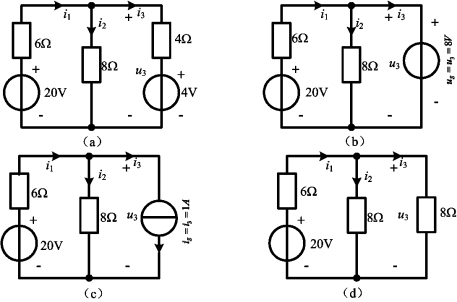
图3-8 替代定理示例
现将支路3分别以us=u3=8V的电压源或is=i3=1A的电流源或![]() 电阻替代,分别如图3-8(b)、图3-8(c)、图3-8(d)所示。替代后,各支路电流为:
电阻替代,分别如图3-8(b)、图3-8(c)、图3-8(d)所示。替代后,各支路电流为:
对于图3-8(b)所示电路有
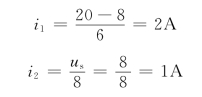
对于图3-8(c)所示电路有

对于图3-8(d)所示电路有
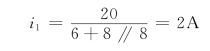
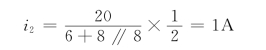
可见,用一个等于该支路电压(或电流或电阻)的电压源(或电流源或电阻)替代该支路后,各支路的电压、电流保持原来值不变。这一结论就是替代定理基本内容,替代定理可表述如下:
在电路中如已求得N1和N2两个一端口电路连接端口处的电压up和电流ip,那么就可用一个us=up的电压源或一个is=ip的电流源或用一个![]() 的电阻来替代其中的一个电路,而使另一个电路的内部电压、电流均维持不变。如图3-9(a)为原电路,分别由N1和N2两个一端口电路连接而成,可以将N2用一个us=up的电压源替代(如图3-9(b))或用一个is=ip的电流源替代(如图3-9(c))或用一个
的电阻来替代其中的一个电路,而使另一个电路的内部电压、电流均维持不变。如图3-9(a)为原电路,分别由N1和N2两个一端口电路连接而成,可以将N2用一个us=up的电压源替代(如图3-9(b))或用一个is=ip的电流源替代(如图3-9(c))或用一个![]() 的电阻来替代(如图3-9(d)),而替代后N1中的电压、电流均维持不变。
的电阻来替代(如图3-9(d)),而替代后N1中的电压、电流均维持不变。

图3-9 替代定理及证明
下面给出替代定理的一般性论证。
设uk,ik(k=1,2,3,…,n)为原电路中各支路电压和支路电流,它们是满足基尔霍夫定律和支路伏安方程的唯一解。当用电流值为ip的电流源替代第p条支路后,由于给定电路的拓扑结构和替代后电路的拓扑结构是相同的,所以,基尔霍夫定律方程将保持不变;除第p条支路外,其他支路的伏安关系也是完全相同的,唯一改变的是第p条支路。在替代后的电路中,第p条支路为一电流源,其值大小规定为is=ip,方向与原来ip的相同,而电流源的端电压可以是任意值。因此,原电路的解仍满足替代后电路的基本方程。由于替代后电路具有唯一解,所以,根据KVL可确定替代部分的支路电压仍为up。因此,原电路中的各支路电压和支路电流完全满足替代后电路的所有条件,这些电压和电流就是替代后电路的唯一解。这就是说,替代前后电路的各支路电压和支路电流是相同的。
对于第p条支路用电压源替代,可以作类似的论证,也可以采用图3-9(e)所示的方法来论证。
先在N2的端子a,d间串接两个电压极性相反,但激励电压值均为us的电压源,令us=up,可见c,b间的电压ucb=0,用一条短路线将两点短接就可得到图3-9(b)所示相同的电路,即用一个us=up的电压源替代N2。
替代定理说明对已知支路的替代,不会改变其他支路结构和电路的KCL、KVL的约束关系,从而不影响整个电路的电压和电流。替代定理不仅适用于线性电路,而且适用于非线性电路以及其他电路。所替代的支路必须为已知支路,可以为有源支路,也可以为无源支路,但一般不应含有受控源或该支路的电压或电流不为其他支路中受控源的控制量。替代定理时常用来对电路进行简化,从而使电路易于分析或计算。
还需要说明的是替代和等效是两个内涵不同的概念。替代表示在特定的条件下,某支路的电压和电流已知时,可用相应的元件来替代该支路,而不影响整个电路在此条件下的电压和电流。而等效是指对外电路来讲在任何情况下均有效。(https://www.daowen.com)
例3-7 电路如图3-10(a)所示,已知u=-4V,i=2A,求i1,i2。
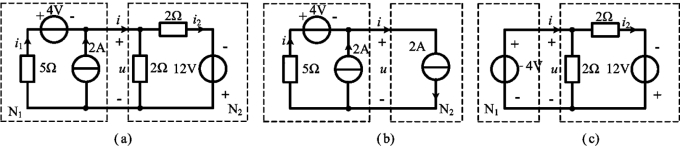
图3-10 例3-7图
解 将网络N2用一个电流为i=2A的电流源替代,得到如图3-10(b)所示电路,对图3-10(b)应用KCL有
i1+2A=2A
所以,i1=0。
将网络N1用一个电压为u=-4V的电压源替代,得到如图3-10(c)所示电路,由图可得
![]()
例3-8 电路如图3-11(a)所示,已知uab=0,求电阻R的值。
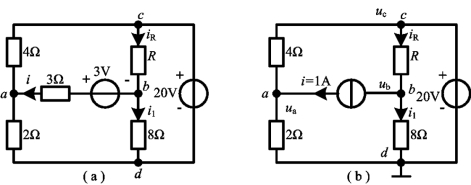
图3-11 例3-8图
解 设ab支路的电流为i,如图3-11(a)所示,故
uab=-3i+3=0
故i=1A。
用1A的理想电流源替代图3-11(a)中的支路ab,如图3-11(b)所示。
选取节点d为参考节点,其余节点a、b、c相对参考节点的电压为ua,ub,uc,故有
uc=20V
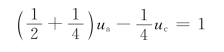
联立求解得
ua=8V
又
uab=ua-ub=0
故有
ub=ua=8V
设各支路电流的大小和参考方向如图3-11(a)所示,故有
![]()
iR=i+i1=1+1=2A
故
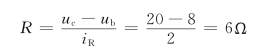
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







