在含有两个或两个以上独立电源的线性电路中，电路中的响应与激励关系又将如何呢？下面以图3-3（a）所示双激励源的线性电路为例来探讨这一问题。图中电压源us和电流源is为电路中的激励，现要求解作为电路中响应的电流i1和电压u2。

根据网孔分析法，可列两网孔方程为

联立求解得

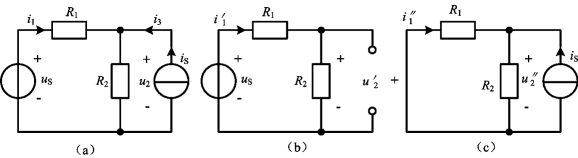
图3-3　叠加定理举例

其中

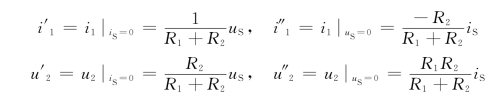
由上式不难看出，i′1和u′2是将原电路中的电流源is置零，仅由电压源us单独作用时，在电路中所产生的电流和电压响应，如图3-3（b）所示；而i″1和u″2是将原电路中的电压源us置零，仅由电流源is单独作用时，在电路中所产生的电流和电压响应，如图3-3（c）所示。

上述讨论表明，由两个独立电源作用共同产生的响应，等于每一个独立电源单独作用时所产生的响应之和。在计算某一独立电源单独作用所产生的电压和电流时，应将电路中其他独立电源置零（电压源用短路代替，电流源用开路代替）。线性电路的这种叠加性称为叠加定理（Superposition Theorem），其表述如下：

在线性电路中，任一支路的电压或电流等于该电路中各个独立电源单独作用时在该支路所产生的电压或电流的代数和。即

式中，y为响应，可以是电流，也可以是电压；n和m分别表示电路中独立电压源和独立电流源的数目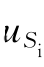； （i=1，2，…，n）及 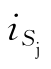（j=1，2，…，m）分别为作用于电路的独立电压源电压及独立电流源电流，系数αi（i=1，2，…，n）及βj=（j=1，2，…，m）为常数，取决于电路的参数及所表示的变量类别，但与独立源无关。由此可见，电路中的响应（电压或电流）实质上是各个独立电源单独作用时响应的线性组合，反映在线性电路中各独立电源的独立性。

特别强调的是，叠加定理只能适用于线性电路，不适用于非线性电路；当一个独立电源作用时，其余独立电源置零，即理想电压源短路，理想电流源开路，而电路的其余结构都不改变；任意独立电源作用时，受控源均要保留，叠加的结果为代数和，因此注意电压或电流的参考方向；由于功率不是电压或电流的一次函数，所以叠加定理不能用于直接计算功率，但可用叠加定理先求支路电压和电流，再用功率的定义式求功率。

例3-3　试用叠加定理求图3-4（a）所示电路中电压u和电流i。

解　因为受控源不是激励源，且具有电阻性，因此用叠加定理求解时，当某一个独立电源单独作用时，其余独立电源均应为零，而保留受控源。

10V的电压源单独作用时的电路如图3-4（b）所示，于是有

（2+1）i′+2i′=10

解得

i′=2A

又

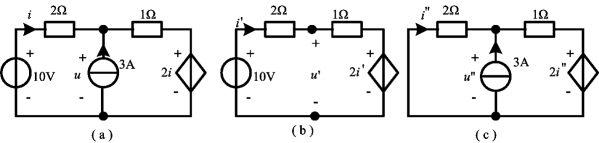
图3-4　例3-3图

u′=1×i′+2i′=1×2+2×2=6V

3A电流源单独作用时的电路如图3-4（c）所示，于是有

2i″+1×（i″+3）+2i″=0

解得

i″=-0.6A

又得

u″=-2i″=-2×（-0.6）=1.2V

根据叠加定理得

u=u′+u″=6+1.2=7.2V， i=i′+i″=2+（-0.6）=1.4A

例3-4　图3-5（a）所示电路，已知当iS=0时，i=1A；当iS=2A，试用叠加定理求电流i。(www.daowen.com)

图3-5　例3-4图

解　该电路中有3个独立电源，若每一个独立电源单独作用一次，需要叠加3次，为此，可采用“独立电源分组”单独作用法来求解。

当iS=0而只有电压源，作用时，其电路如图3-5（b）所示，根据题意，有i′=i=1A。

当只有电流源iS=2A单独作用时，其电路如图3-5（c）所示，所以有

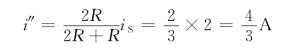
根据叠加定理得

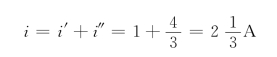
例3-5　图3-6所示电路，=10V，=15V，当开关S在位置1时，毫安表的读数为I′=40mA；当开关S在位置2时，毫安表的读数为I″=-60mA，求开关S打在位置3时毫安表的读数。

解　设流过电流表的电流为I，根据叠加定理有

I=K1iS+K2uS

当开关S在位置1时，uS=0，I′=40mA，所以有

40=K1iS

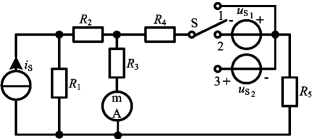
图3-6　例3-5图

当开关S在位置2时，I″=-60mA，所以有

-60=K1iS+K2uS=40+10K2

解得：K2=-10。

所以，当开关S在位置3时，，可得关系式

例3-6　图3-7所示网络N为线性含源网络。已知当，时，响应Ux=80V；当，时，响应Ux=0；当时，响应Ux=-40V。求当时，响应Ux的值。

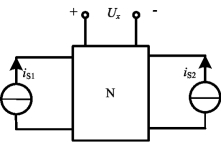
图3-7　例3-6图

解　根据叠加定理可知，响应Ux可分解为3部分，即

Ux=U′x+U″x+U‴x

其中，U′x由产生，并与成正比，即；U″x由产生，并与成正比，即；U‴x由网络N中的独立电源产生。故

代入已知的参数有

80=8α+12β+U‴x

0=-8α+4β+U‴x

-40=0α+0β+U‴x

可求得

α=0 β=10 U‴x=-40V

所以，当==20A时，响应Ux的值为