线性（Linearity）是指比例性（Proportionality）和相加性（Superposition）的组合。比例性要求若输入（或称激励（Excitation））乘以一个常数，那么输出（或称响应（Response））也乘以一个相同的常数。例如对于电阻元件，按欧姆定律，输入电流i与输出电压u的关系为u=Ri，若电流乘以k，则电压也相应地增加了k倍，即kRi=ku；相加性要求对各个输入和的响应等于每个输入的单独响应之和。仍以上述电阻元件为例，当输入分别为i1，i2时，分别有输出u1=Ri1，u2=Ri2；若输入为i1+i2，则输出有u=R（i1+i2）=Ri1+Ri2=u1+u2。

可见，电阻元件的电压电流关系既满足比例性也满足相加性，因此，电阻元件是线性元件（Linear Element）。一般而言，若一个电路满足比例性和相加性，则称该电路为线性电路（Linear Circuit）。线性电路只含有线性元件、线性受控源和独立电源等。独立电源是非线性二端元件，但它是电路的输入，对电路起激励作用，电压源的电压和电流源的电流与所有其他元件的电压、电流所扮演的角色完全不同，前者为激励，而后者只是激励引起的响应。因此，尽管电源是非线性的，但只要电路的其他部分是由线性元件组成，那么响应和激励之间将存在着线性关系。

齐次定理（Homogeneity Theorem）：在线性电路中，当所有激励同时增大或缩小K（K为实常数）倍时，对应的响应也将增大或缩小K倍。即

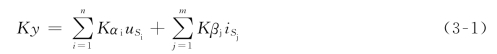
式中，（i=1，2，…，n）及（j=1，2，…，m）分别为作用于电路的各独立电压源电压及各独立电流源电流，αi（i=1，2，…，n）及βj=（j=1，2，…，m）为常数，取决于电路的参数及所表示的变量类别，但与独立源无关。

齐次定理反映在线性电路中激励和响应的比例关系，它只适用于线性电路，不适用于非线性电路。其中的激励是指独立电源，响应是指电压或电流；当电路中只有一个激励时，响应将与激励成正比。只有当全部激励同时增大或缩小K倍时，响应才同时增大或缩小K倍，否则将导致错误的结果。齐次定理不能用于功率的计算。

例3-1　求图3-1所示电路中当us=12V和us=24V时的电流i0。

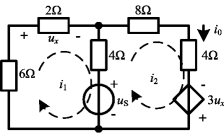
图3-1　例3-1图

解　对两个回路分别应用KVL得

12i1-4i2=-us

-4i1+16i2=3ux+us

而

ux=2i1

联立求解得

(www.daowen.com)

当us=12V时

当us=24V时

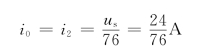
这说明，若电源电压是原来的2倍，则电流i0也增加原来的2倍。这正是线性电路齐次性的基本要求。

例3-2　设i0=1A，用线性定理求图3-2所示电路中的实际电流值i0。

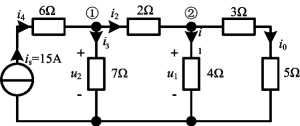
图3-2　例3-2图

解　若i0=1A，则u1=（3+5）i0=8V，且，对节点1应用KCL，有

i2=i1+i0=2+1=3A

则有

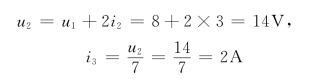
对节点2应用KCL有

i4=i2+i3=3+2=5A

所以is=i4=5A，这就是说若要i0=1A，则电流源is应为5A，图3-2所示电路为线性电路，若电流源is=15A，根据线性电路的齐次定理，则实际得到电流i0为i0=3A。