1.反相放大器

图2-44（a）表示一个由运放和电阻构成的反相放大电路，该电路同相端接地，输入电压ui通过电阻R1接到反相输入端，反馈电阻Rf接在反相输入端和输出端之间。

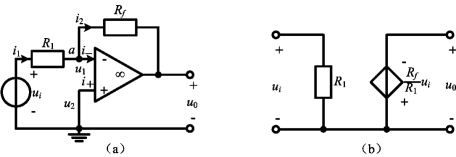
图2-44　反相放大器及其等效电路

（a）反相放大器；（b）等效电路

对于理想运放有

i+=i-=0

u1=u2=0

对节点a应用KCL有

i1=i2

而

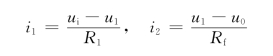
所以

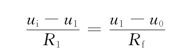
解得

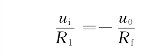
即

由式（2-58）可知，当Rf＞R1时，输出电压u0的幅度比输入电压ui的幅度大，该电路是一个电压放大器，式中的负号表明输出电压与输入电压的极性相反，故称之为反相放大器（Inverting Amplifier）。反相放大器的增益只取决于接到运放上的外部电路元件，可用在电流—电压转换器的电路中。为了保证该运放工作于线性区，应使输入电压的幅度限制在一定的范围内，即应满足以下条件

从式（2-58）来看，反相放大器等效电路如图2-44（b）所示。

2.同相放大器

如图2-45所示，输入电压ui直接接到同相输入端，电阻R1接在反相端和地之间。

对于理想运放有

i+=i-=0 u1=u2=ui

对节点a应用KCL有

i1=i2

而

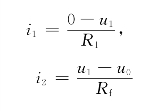
所以

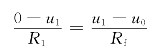
解得

由式（2-60）可知，输出电压u0的幅度比输入电压ui的幅度大，该电路也是一个电压放大器，输出电压与输入电压的极性相同，故称之为同相放大器（Noninvering Amplifier）。同相放大器的增益也只取决于接到运放上的外部电路元件。为了保证该运放工作于线性区，应使输入电压的幅度限制在一定的范围内，即应满足以下条件

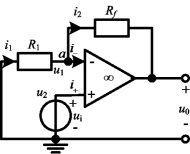
图2-45　同相放大器

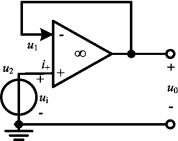
图2-46　电压跟随器

若反馈电阻Rf=0（短路）或R1=∞（开路）或既Rf=0又R1=∞，此时式（2-60）变为u0=ui，即此时的输出电压和输入电压一样，则图2-45电路变为图2-46所示，该电路称为电压跟随器（Voltage-follower）或称为单位增益放大器。由于该电路的输入电阻为无穷大而输出电阻为零，将它插入两个双口网络之间时，既不会影响网络的转移特性，又能对网络起到隔离作用，因此，又称它为缓冲器（Bumper）或隔离器（Isolator）。如图2-47所示电路中，图（a）为把负载RL直接接入，而图（b）是将负载RL通过电压跟随器接入，两者情况下的输出电压均为，但后者负载电阻的作用被“隔离”了。

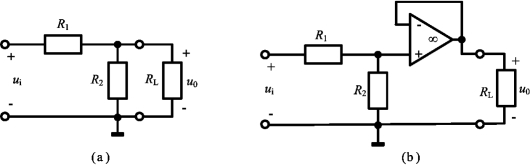
图2-47　电压跟随器隔离作用

3.相加放大器

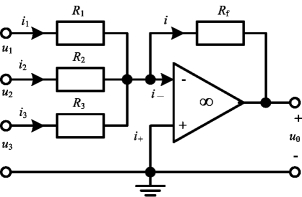
图2-48　加法运算电路

如图2-48所示，输入电压u1，u2，u3都接到反相输入端，同相端直接地，它是反相放大器的一个变种。反相放大器同时输入多个信号时，可构成相加放大器（Summing Amplifier）。

考虑理想运放的“虚断”特性，图中节点a的KCL方程为

i=i1+i2+i3

又由理想运放的“虚短”特性可知节点a的电位ua=0，所以

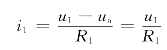
同理

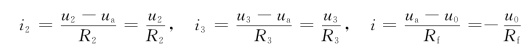
因此，节点a的KCL方程可写为

解得

如果满足条件：R1=R2=R3=Rf，上式可变为

由此可见，此电路的功能是把各输入电压相加并反相输出，因此，一般此电路称为加法放大器。

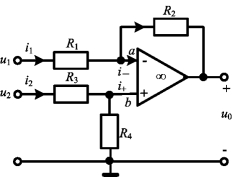
图2-49　差分放大器

4.差分放大器

图2-49所示电路中，两输入电压u1，u2分别接到反相输入端和同相端。由理想运放的“虚断”特性，对于图中节点a和b有

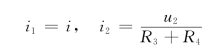
节点b电压为

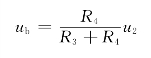
又由“虚短”特性可确定节点a电压为

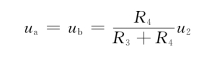
所以

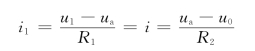
将ua代入上式，并整理得

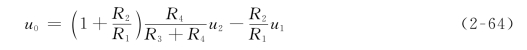
结果表明，该电路将输入电压分别按比例放大，然后求差后输出，因此，该电路构成一个差分放大器（DifferentialAmplifier）。

如果满足条件：R1=R2=R3=R4=R，式（2-63）可变为

结果为两输入信号之差，因此，一般把该电路称为减法器（Subtractor）。

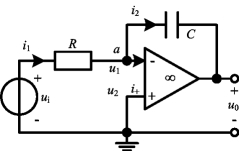
图2-50　积分运算电路

5.积分器

积分器（Integrator）和微分器（Differentiator）是用储能元件构成的运算放大器，通常含有电阻和电容，由于绕线电感器的体积大和价格贵等缺点而较少采用。运放积分器的输出正比于输入信号的积分，它有很多应用，特别是在模拟计算机中。

理想的积分器如图2-50所示。它实质上就是将图2-44（a）中反相放大器的反馈电阻Rf用一个电容器取代。由理想运放的“虚断”和“虚短”特性，对于图2-50中节点a应用KCL得

i1=i2

而

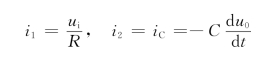
所以有

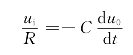
整理得

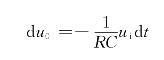
对两边积分得

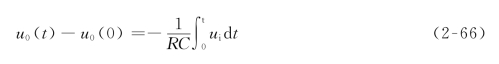
设u0（0）=0，则

上式表明，图2-50电路的输出电压正比于输入电压的积分，因此该电路实现了对输入信号的积分运算。运算积分放大器要注意运行在线性范围内，所以在实际电路中，还有一个反馈电阻以降低其直流增益和避免饱和。(www.daowen.com)

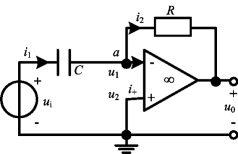
图2-51　微分运算电路

6.微分器

微分器也是一个运算放大器电路，它的输出正比于输入信号的变化率。图2-51所示电路即为一个微分器。在图中节点a处，根据KCL，同时利用理想运放的“虚断”和“虚短”特性，得

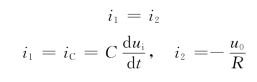
所以有

即输出是输入的微分。要注意的是，这种微分电路从电子学角度来讲是不稳定的，任何电路中的电子噪声将被微分器放大。所以图2-51微分电路在实践中很少使用。

例2-19　求如图2-52所示单口网络的输入电阻Rab。

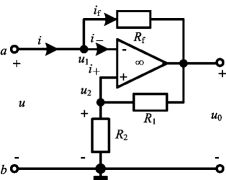
图2-52　例2-19图

解　利用外加电源法求出a、b两端的伏安关系，从而求得输入电阻Rab。利用理想运算放大器的“虚断”和“虚短”特点有

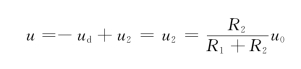
得到

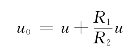
将上式代入KVL方程

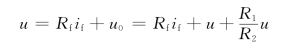
解得

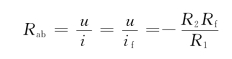
当R1=R2时

Rab=-Rf

上式表明该电路可将正电阻Rf变换为一个负电阻。为了实现负电阻，要求运放必须工作在线性区，即u0＜Usat，从而可求得负电阻上的电压应满足

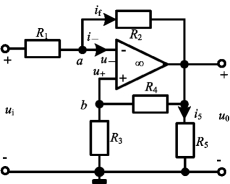
图2-53　例2-20图

例2-20　图2-53所示电路，已知R1=R3=R4=1kΩ，R2=R5=2kΩ，ui=1V，求i5。

解　对节点a、b列KCL方程为

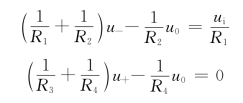
将电路参数代入上式得

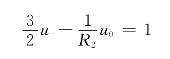
2u+-u0=0

又

u+=u-

联立求解得

u0=4V

故得

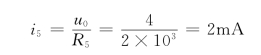
例2-21　图2-54所示电路，求输出端电压u0。

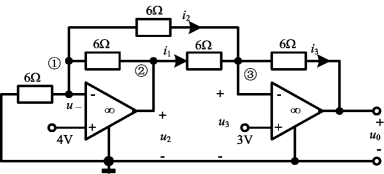
图2-54　例2-21图

解　对3个独立节点列KCL方程为

u=u-=u+=4V

u3=u-=u+=3V

联立求解得

u2=9V

故得

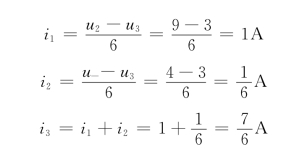
故

例2-22　设计一个两输入u1和u2的运算放大电路，使其输出u0=-5u1+3u2。

解　可以有两种设计方法。

方法一：只用一个运算放大器。电路如图2-55所示。将u0=3u2-5u1和式（2-64）比较可得

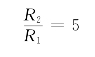
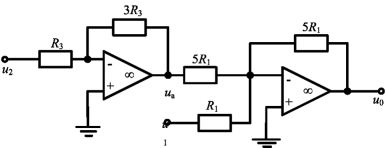
图2-55　例2-22图

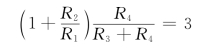
因此有

R2=5R1， R3=R4

若选取R1=10kΩ和R3=20kΩ，R2=50kΩ和R3=20kΩ。

方法二：采用二个运算放大器来实现：将一个反相放大器和一个双输入反相相加器串接起来，如图2-54所示。

对相加器有

u0=-ua-5u1

对反相器有

ua=-3u2

联立上述2个式，得u0=3u2-5u1，满足设计要求。

例2-23　用运算放大器可以实现受控源，试将图2-56所示电路以一个受控源形式表示，并求其控制系数。

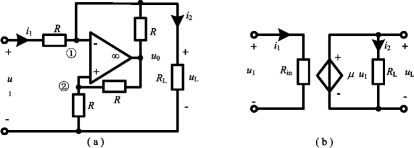
图2-56　例2-21图

解　根据节点分析法，列出节点①、②方程，并应用理想运算放大器的“虚断”特性得

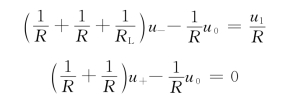
再应用理想运放的“虚短”特性，有u+=u-=uL，联立求解得

又因为

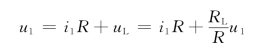
故

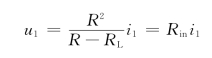
其中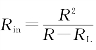，为受控源的输入电阻；而为输出电路端电压，所以，图2-56（a）电路可以用一个电压控制的受控电压源表示，其控制系数为 ，等效电路如图2-55（b）所示。

例2-24　设计一个模拟计算机来解下面微分方程

假设u（0）=-4，u′o（0）=1。

解　第一步求一阶微分，由微分方程，得

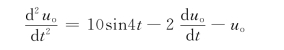
求解上式要求进行相加、比例和积分运算。对上式两边积分有

式中，u′o（0）=1。用图2-57（a）所示的相加积分器来实现上式，且选择恰当的电阻和电容的值，使项中的RC=1。相加积分中的其他项，由电路做相应的运算。

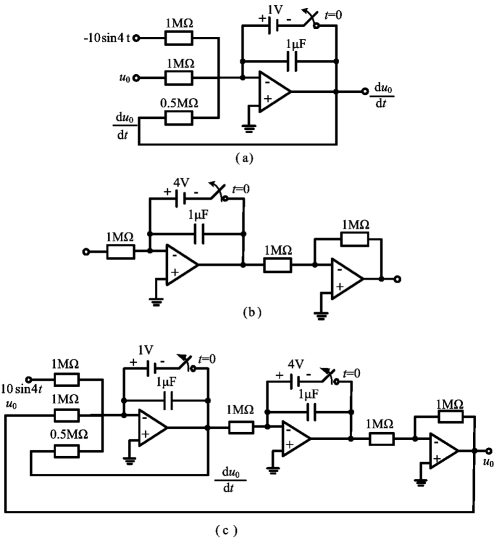
图2-57　例2-24图

初始条件，用一个1V的电池，带一个开关接在电容器的两端来实现，如图2-57（a）所示。

第二步求输出uo。对积分、并反相，其结果为

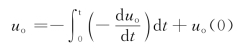
上述关系由图2-56（b）所示的电路来实现，图中用一个-4V电池来满足初始条件。图2-57（a）和图2-57（b）合起来得到一个完整的电路，如图2-57（c）所示。加上10sin4t的输入且在t=0时刻打开开关，就得到输出波形。