类似于选用完备的独立电流变量作为求解对象，也可以选用完备的独立电压变量作为求解对象。由于受KVL的约束，一个电路的各支路电压并非都独立，对于一个具有n个节点的电路，独立的电压变量只有n-1个。在电路中任选一个节点作为参考点，其余的每一个节点到参考点的电压降，就称为这个节点的节点电压（Node Voltage）。显然，一个具有n个节点的电路，有n-1个独立的节点电压。电路中任一支路电压等于该支路连接的两个节点的节点电压之差，如图2-35所示电路中A、B为任意两节点，根据KVL，有uAB+uB-uA=0，所以，有uAB=uA-uB。因此，只要求出n-1个节点电压，所有支路电压根据KVL随之而确定，所以，节点电压是一组完备的独立电压变量，可作为电路求解对象。

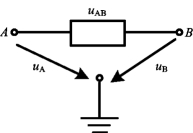
图2-35　节点电压与支路电压关系

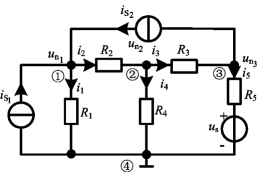
图2-36　节点分析法图例

以图2-36电路为例来说明节点分析法的基本思想。图2-36电路中有4个节点，分别标称为①、②、③、④，若选第④个节点为参考点，则其他3个节点相对参考节点的电压分别记为，，称为对应节点的节点电压。根据KCL，可列写出3个节点的方程如下

把支路电流用节点电压表示

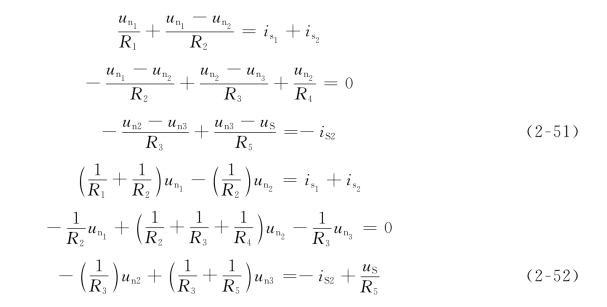
令，k=1，2，3，4，5，则式（2-51）简记为

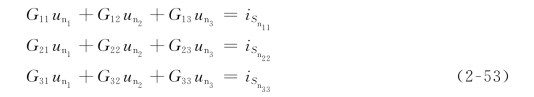
式中，G11=G1+G2——节点1的自电导（Self Conductance）；

G22=G2+G3+G4——节点2的自电导；

G33=G3+G5——节点3的自电导；可见节点的自电导等于接在该节点上所有支路的电导之和。

G12=G21=-G2——节点1与节点2之间的互电导（Mutual Conductance），G23=G32=-G3为节点2与节点3之间的互电导。可见互电导为接在节点与节点之间所有支路的电导之和，总为负值。

流入节点1的电流源电流的代数和为流入节点3的电流源电流的代数和。其中，流入节点取正号，流出节点取负号。

由节点方程求得各节点电压后即可求得各支路电压，各支路电流可用节点电压表示：

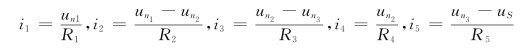
式（2-53）为节点方程的一般形式，适合于具有三个独立节点电路。对于具有n-1个节点的电路，节点方程的一般形式为：

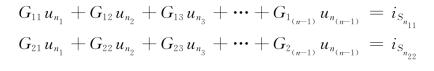
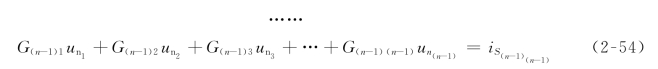
由于各节点电压都一律假定为电压降，因而各互导都是负值。式（2-54）为节点方程一般式，可用来研究线性电路的一般性质。这种以节点电压为独立变量的分析方法称为节点分析法（Node Analysis Method），对平面和非平面电路都适用。

综上分析，节点分析法的一般步骤为：

（1）画出电路图，选定参考节点，标定n-1个独立节点，设定各独立节点的电压大小和“+”，“-”极性。一般都是取各独立节点为“+”极端，参考节点为“-”极端；

（2）对n-1个独立节点，以节点电压为未知量，列写其KCL方程；

（3）联立求解上述得到的方程组，得到n-1个独立节点电压；

（4）设定各支路电压大小和参考极性，通过节点电压求各支路电压；

（5）设定各支路电流大小和参考方向，根据各支路电压求各支路电流；

（6）根据（4）、（5）所得结果求各支路功率。

例2-15　列出图2-37所示电路中的节点方程。

解　图中有3个节点，选③号节点为参考节点，设节点①、②的电压分别为，，则节点方程为　

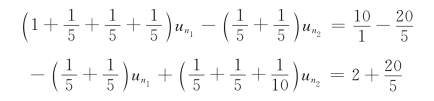
整理得

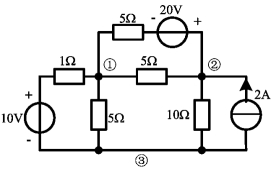
图2-37　例2-15图

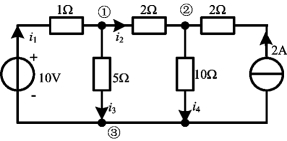
图2-38　例2-16图

例2-16　用节点法求图2-38所示电路中各支路电流。

解　节点编号如图中所示，选③号节点为参考节点，设节点①、②的电压分别为，。因为与电流源串接的任何元件可看成是多余的，因此，图中与2A电流接的2Ω电阻不计入自电导中。所以节点①、②的方程为(www.daowen.com)

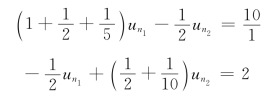
解上述方程得

各支路电流为

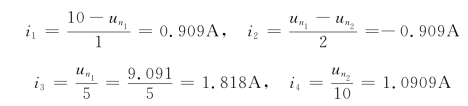
例2-17　用节点法求图2-39所示电路中电流IS和I0。

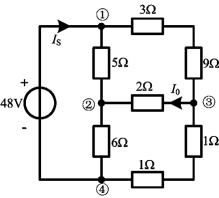
图2-39　例2-17图

解　该电路中48V电压源无电阻与之串联而独占一条支路，称为无伴电压源或纯电压源支路。对于这样的支路，如果按列写节点电压方程的一般原则列写方程，则会遇到无伴电压源支路的电导为∞的棘手问题。因此，对于这样的问题只能从节点分析法的实质出发，寻求合理的解决方法。通常是选取与无伴电压源支路相连接的节点之一作为参考节点，这样，另一节点的电压即为电压源的电压，成为已知量，则该节点的节点方程就可不用列写，这样既减少了一个方程，同时，又避开了无伴电压源电导为∞的问题；如果电路中含两个或以上的无伴电压源支路，或虽然只含有一个无伴电压源支路，但参考节点已被限制而不是该无伴电压源支路的两个节点之一，则可增设无伴电压源支路电流I为未知量，把它视作电流源看待，然后由无伴电压源的约束关系，再增补一个方程，从而使方程数和未知量数相同。

方法一：选④号节点为参考节点，设节点①、②、③的电压分别为，，。则

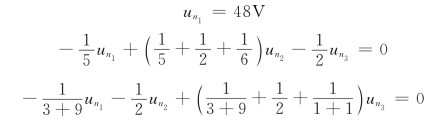
求解得

则

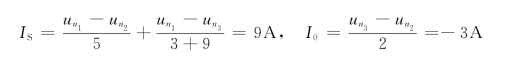
方法二：选③号节点为参考节点，设节点①、②、④的电压分别为，，。则

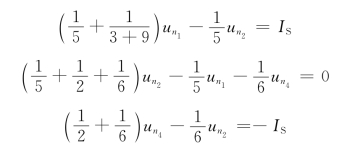
由无伴电压源的约束关系，可再增补一个方程

而

方程数和未知量数相同，可求解。解上述方程组可得

IS=9A， I0=-3A

例2-18　用节点法求图2-40所示电路中电压u，并求4V电压源发出的功率。

解　该电路中含有受控电源，在分析时可先将受控电源视为独立电源，按节点分析法的基本原则列写节点方程，然后将方程中受控电源的控制量用节点电压表示，并对方程进行整理。

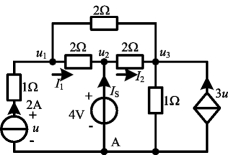
图2-40　例2-18图

选节点A为参考节点，其余3个节点电压分别为u1，u2，u3，如图中所示。与2A电流源相串联的1Ω电阻可视为多余，则节点电压方程为　

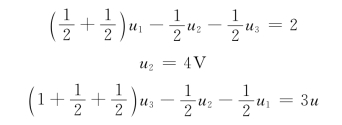
再由图可知

u=1×2+u1=2+u1

以上4式联立求解得

u1=48V， u2=4V， u3=88V， u=50V

又

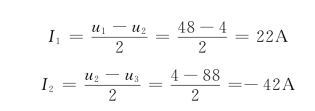
IS=I2-I1=-22-42=64A

所以，4V电压源发出的功率为

P=4IS=4×（-64）=-256W

综上所述，节点分析法就是选定某个节点作为参考节点，其他节点相对于该参考节点的电压即节点电压作为电路待求变量，以KCL和支路伏安关系为基本依据列写电路方程，从而求解电路的一种分析方法。节点分析法的物理意义反映了在各电流源的共同作用下，流出节点电流的代数和等于流入节点的电流源电流的代数和。当利用节点法求只含独立电源电路时，如果电路含有理想电压源，则一般有3种处理方法：一种是仅含有理想电压源与电阻的串联支路，则可进行电源等效变换，使之变换为一个实际电流源模型；另一种是当电路仅含有一个理想电压源支路时，可选合适的节点作为参考节点，使该理想电压源成为已知节点电压，而仅对其余节点列写方程；第三种是设理想电压源的电流为I，将此电流暂当作电流源电流一样列写方程，然后利用理想电压源与相应节点电压的关系补充方程，从而求得待求量。当电路中含有受控源时，可先将受控电源视为独立电源，按节点分析法的基本原则列写节点方程，然后将方程中受控电源的控制量用节点电压表示，并对方程进行整理。