1.理想电压源的串联和并联
图2-13(a)为n个理想电压源的串联,如图2-13(a)所示,根据KVL,有
![]()
由式(2-25)可见,n个串联的理想电压源,可以用一个理想电压源等效替代,等效电压源的激励电压为串联的各电压源电压的代数之和,如图2-13(b)所示。如果uSk的参考方向与图2-13(a)中uS的参考方向一致时,式(2-25)中uSk的前面取“+”号,否则不一致时取“-”号。
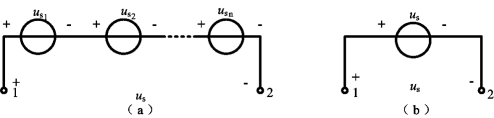
图2-13 电压源的串联及其等效电路
只有激励电压相等且极性一致的电压源才允许并联,否则违背KVL。其等效电路为其中任一电压源,但这个并联组合向外部提供的电流在各个电压源之间如何分配则无法确定。如图2-14为两个相同电压源的并联及其等效电路。
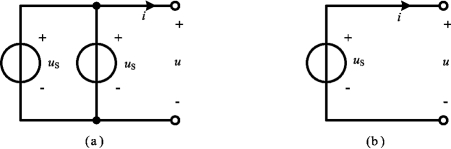
图2-14 两相同电压源的并联及其等效电路
若电压源与某支路相串联,如图2-15(a)所示,根据KVL,有
![]()
等效电路如图2-15(b)所示。
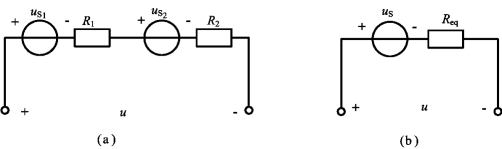
图2-15 电压源与某支路的串联及其等效电路
若电压源与支路相并联,如图2-16(a)所示,其中N′为任意元件。这一单口电路的VAR为
![]()
由于N′与电压源并联,它的存在并不影响端口的电压,端口电压总是等于电压源的电压。但N′存在会使电压源的电流发生改变,由于电压源的电流可为任意值,因此端口电流仍为任意值。所以,图2-16(a)所示一端口电路可以用图2-16(b)所示的等效电路来代替,亦即为电压源本身。从端口等效的观点来看,N′为多余元件。其实,从等效观点来看,与电压源并联的单口电路也是多余的。
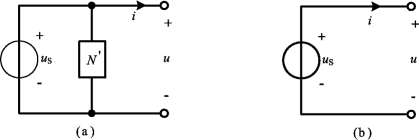
图2-16 电压源与某支路并联及其等效电路
2.理想电流源的串联和并联
图2-18(a)为n个电流源的并联,根据KCL有
![]()
由式(2-28)可见,n个并联的理想电流源,可以用一个理想电压源等效替代,等效电压源的激励电流为并联的各电流源电流的代数之和,如图2-18(b)所示。如果iSk的参考方向与图2-18(a)中iS的参考方向一致时,式(2-28)中iSk的前面取“+”号,否则不一致时取“-”号。
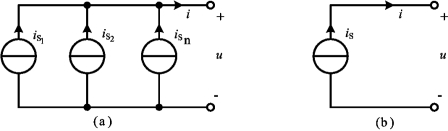
图2-17 电流源并联及其等效电路
只有电流源的电流都相等且方向一致的电流源才允许串联,否则违背KCL。其等效电路为其中任一电流源,但这个串联组合向外部提供的电压在各个电流源之间如何分配则无法确定。如图2-18为两个相同电流源的串联及其等效电路。
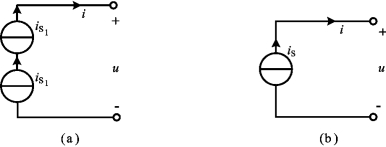
图2-18 两相同电流源的串联及其等效电路
若电流源与支路相串联,如图2-19(a)所示,其中N′为任意元件。这一单口网络的VAR为
![]()
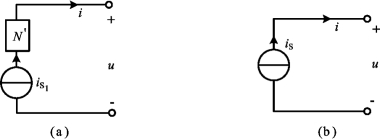 (https://www.daowen.com)
(https://www.daowen.com)
图2-19 电流源与某支路串联及其等效电路
由于N′与电流源串联,它的存在并不影响端口的电流,端口电流总是等于电流源的电流。但N′存在会使电流源的电压发生改变,由于电流源的电压可为任意值,因此端口电压仍为任意值。所以,图2-19(a)所示单口电路可以用图2-19(b)所示的等效电路来代替,亦即为电流源本身。从端口等效的观点来看,N′为多余元件。其实,从等效观点来看,与电流源串联的单口电路也是多余的。
3.实际电源的两种模型及其等效变换
实际电源的电压(或电流)往往会随着电源电流(或电压)的增加而下降。图2-20(a)和(c)表示电压表、电流表和可变电阻器测量直流电源VAR特性曲线的实验电路,测得两种典型VAR特性曲线如图2-20(b)和(d)所示。
由图2-20(b)可见,特性曲线与电压轴的交点Uoc表示电源不接负载时的开路电压,随着电流的增加,电压沿直线下降,当电流超过某一额定值In后,电压急剧下降。为了得到电源在正常工作时的电路模型,将直线部分延长,与电流轴交点为(Isc,0)。该直线方程为
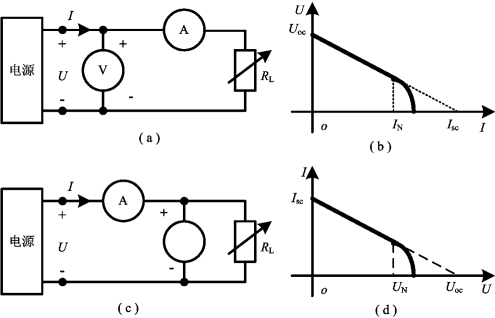
图2-20 直流电源VAR特性曲线测量
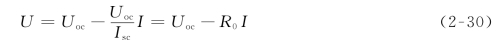
式中,![]() ——电源内电阻,由直线的斜率确定。
——电源内电阻,由直线的斜率确定。
根据式(2-30)得到的电路模型如图2-21(a)所示,它为电压源Uoc和电阻R0的串联组成。
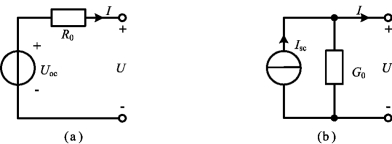
图2-21 直流电源的两种电路模型
同理,图2-20(d)所示曲线与电流轴的交点Isc表示电源短路时的短路电流,相应的直线方程为
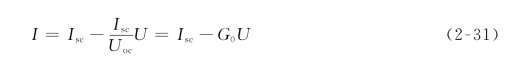
式中,![]() ——电源内电导,由直线的斜率确定。
——电源内电导,由直线的斜率确定。
根据式(2-31)得到的电路模型如图2-21(b)所示,它为电流源Isc和电导G0的并联组成。
图2-21(a)和(b)所示即为实际电源的两种模型,它们在满足一定条件时可以相互的等效变换。下面我们来推导它们等效变换的条件。
将式(2-31)改写如下

由式(2-30)和式(2-32)可知,若令![]() ,Isc=G0Uoc,则式(2-30)和式(2-32)所表示VAR完全相同,根据等效的定义,图2-21(a)和(b)所示两个电路对外来说是等效的,所以,两种实际电源模型等效变换的条件为:
,Isc=G0Uoc,则式(2-30)和式(2-32)所表示VAR完全相同,根据等效的定义,图2-21(a)和(b)所示两个电路对外来说是等效的,所以,两种实际电源模型等效变换的条件为:![]() ,Isc=G0Uoc。
,Isc=G0Uoc。
例2-5 用电源等效变换求图2-22(a)所示电路的等效电路及其端口的伏安关系。
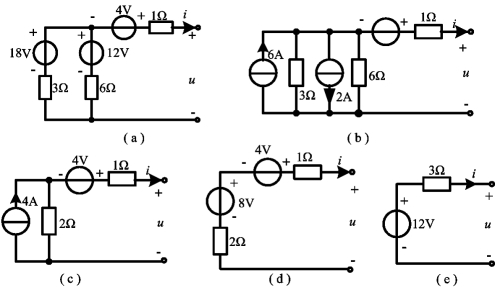
图2-22 例2-5图
解 先将18V电压源和3Ω电阻串联的支路等效变换为6A电流源和3Ω电阻的并联,再将12V电压源和6Ω电阻串联的支路等效变换为2A电流源和6Ω电阻的并联,如图2-22(b)所示。再将6A和2A并联的电流源等效变换为一个4A的电流源,将6Ω和3Ω的并联电阻等效变换为一个2Ω的电阻,如图2-22(c)所示。再将4A的电流源和2Ω电阻的并联支路等效变换为8V电压源和2Ω电阻的串联,如图2-22(d)所示。最后得到如图2-22(e)所示的等效电路。其端口的伏安关系为
u=12-3i
例2-6 用电源等效变换求图2-23(a)所示电路电流I。
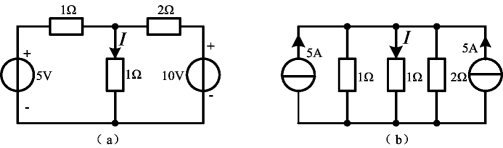
图2-23 例2-6图
解 用电源等效变换方法,先将图2-23(a)所示电路中电压源与电阻的串联等效变换为电流源与电阻的并联,如图2-23(b)所示,所以电流I为
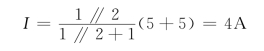
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






