电阻的连接一般有串联、并联和混联等几种形式，3个电阻还可连接为△形和Y形形式。此处将讨论它们的等效变换。

1.电阻的串联

若流过各个电阻的电流为同一电流，则这些电阻即为串联连接，简称串联（Series Connection）。图2-4（a）所示即为n个电阻的串联，因为流过每个电阻中的电流为同一电流i。应用KVL有

u=u1+u2+u3+…+un

图2-4　电阻的串联及其等效电路

由于每个电阻的电流均为i，有u1=R1i，u2=R2i，u3=R3i，…，un=Rni，代入上式，得

u=（R1+R2+R3+…+Rn）i=Reqi

此即为图2-4（a）所示端口1-1′的伏安关系，其中

电阻Req为这些串联电阻的等效电阻（Equivalent Resistance）。这就是说n个电阻的串联等效为一个电阻，等效电阻大小为n个串联电阻之和，如图2-4（b）所示。显然，等效电阻必大于任一个串联的电阻。

串联时，各电阻上的电压为

可见，串联的每个电阻，其电压与电阻值成正比。式（2-2）称为电压分配公式，或称分压公式（Principle of Voltage Division）。

由于Req=R1+R2+R3+…+Rn，在等式两边同乘以i2得

i2Req=i2R1+i2R2+i2R3+…+i2Rn

根据电阻功率定义式有

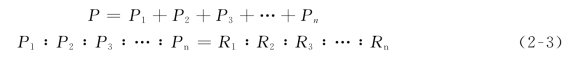
式（2-3）说明，n个串联电阻所消耗的功率总和等于这n个串联电阻的等效电阻所消耗的功率，各电阻的功率之比等于对应的电阻之比。

2.电导的并联

若加在各个电导上的电压为同一电压，则这些电导即为并联连接，简称并联（Parallel Connection）。图2-5（a）所示即为n个电导的并联，因为加在每个电导两端的电压为同一电压u。由于电压相等，总电流可根据KCL求出。图2-5（a）所示电路中，端口1-1′的伏安关系为

其中

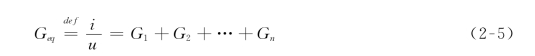
图2-5　电导的并联及其等效电路

Geq为n个电导并联后的等效电导（Equivalent Conductance）。这就是说，n个电导的并联等效为一个电导，等效电导大小为n个串联电导之和，如图2-5（b）所示。显然，等效电导必大于任一个串联的电导。并联后的等效电阻为，所以并联后等效电阻小于任一个并联的电阻。

并联时，各电导中的电流为

可见，并联的每个电导其电流与电导值成正比。式（2-6）称为电流分配公式，或称分流公式（Principle of Current Division）。

由于Geq=G1+G2+G3+…+Gn，在等式两边同乘以u2得

u2Geq=u2G1+u2G2+u2G3+…+u2Gn

根据电阻功率定义式有

式（2-7）说明，n个并联电导所消耗的功率总和等于这n个并联电导的等效电导所消耗的功率，各电导的功率之比等于对应的电导之比。

例2-3　计算图2-6所示电路的等效电阻Rab。

解　3Ω和6Ω电阻的两端均分别接到c和b点，所以为并联关系，其等效电阻为

(www.daowen.com)

12Ω和4Ω电阻的两端均分别接到d和b点，所以为并联关系，其等效电阻为

图2-6　例2-3图

1Ω和5Ω电阻为串联关系，其等效电阻为1Ω+5Ω=6Ω

经过上述化简后，图2-5（a）所示电路可简化为图2-5（b），由图（b）可求得电路的等效电阻为

Rab=10Ω+2Ω∥（1Ω+3Ω∥6Ω）=11.2Ω

3.电阻Y形连接与△形连接的等效变换

将三个电阻的一端连在一起，另一端分别与外电路的三个节点相连，构成星形连接（Wye Connection），又称Y形连接或T形连接，如图2-7（a）所示。若将三个电阻首尾相接，连接成一个三角形，三角形的三个顶点引出三条线与外部电路连接，这样的连接称之为三角形连接（Delta Connection），又称为△形连接或∏形连接，如图2-7（b）所示。

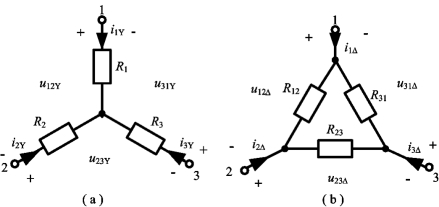
图2-7　电阻的Y形连接和△形连接

由图2-7（a）可得

由图2-7（b）可得

根据等效的定义，要使图2-7（a）所示连接和图2-7（b）所示连接等效，则有

根据等效条件，比较式（2-8）和式（2-9），可得

式（2-11）即为电阻三角形连接等效变换为电阻星形连接时的等效条件，可概括为

当R12=R23=R31=RΔ时有

由式（2-11）可解得

式（2-14）即为电阻星形连接等效变换为电阻三角形连接时的等效条件，可概括为　

当R1=R2=R3=RY时有

上述将电阻三角形连接等效变换为电阻星形连接或将电阻星形连接等效变换为电阻三角形连接统称为Y-△等效变换（Wye-delta Transformation）。

例2-4　计算图2-8（a）所示电路中负载电阻RL消耗的功率。

解　将连接成三角形网络的三个30Ω电阻等效变换为星形连接网络，如图2-8（b）所示，由于三个电阻大小相同，所以，其值为，再利用电阻的串联、并联公式，求出串联的等效电阻，得到如图2-8（c）所示电路，再将图2-8（c）所示电路中三角形连接网络等效变换为星形连接网络，得到如图2-8（d）所示电路。由图2-8（d）所示电路即可求得流过负载电阻的电流为

iL=1A

所以，负载电阻RL消耗的功率为

PL=RL=40×12=40W

图2-8　例2-4图