1.一端口电路的定义及伏安关系

一个电路如果只有两个与外部电路连接的端钮，且两个端钮上的电流为同一电流，则这样的两个端钮即构成电路的一个端口（Port），简称一端口或单口（Oneport），相应的电路称为一端口电路或单口电路（One-port Circuit）。在电路分析中，也常常将电路称之为网络（Network），所以只有两个端钮与外部连接的电路也称为一端口网络或单口网络（One-port Network）。图2-1（a）中的a、b两端即构成一个端口，此电路即为一端口电路或称单口电路或称单口网络或称为二端网络（Two-terminal Network），图2-1（b）、（c）为两个简单一端口电路。其中，端口上的电压u和电流i分别称为端口电压和端口电流。端口电压u与端口电流i的关系称为端口的伏安关系（Volt-Ampere RelationorU-IRelation of Port）。本书采用一端口电路这个名词。

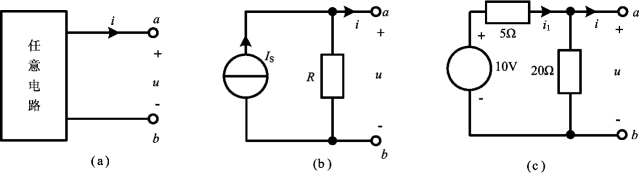
图2-1　端口与一端口电路

（a）一端口定义；（b）、（c）一端口示例

显然，一个二端元件是一个最简单的二端电路。一个二端元件有它的外部特性，如电阻元件的伏安特性，电容元件的库伏特性，电感元件的韦安特性等，且这种特性是由该元件本身所确定的，与外接电路无关。同样，一个一端口电路也有它的外部特性，而且也是由该一端口电路本身所确定的，与外接电路无关。一端口电路的外部特性常用它的端口电压和端口电流之间的伏安关系来表示的。

例2-1　试求图2-1（b）、（c）所示一端口电路的伏安关系。

解　对于图2-1（b），用应KCL和元件的伏安关系，有

u=R（Is-i）=RIs-Ri

对图2-1（c），应用KVL和元件的伏安关系，有

10=5i1+u

u=20（i1-i）

消去i1可得u=8-4i。

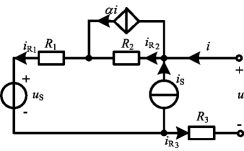
图2-2　例2-2图

例2-2　试求图2-2所示一端口电路的伏安关系。(www.daowen.com)

解　设想在电路两端施加一个电流源i，根据KCL有

根据KVL有

联立上述表达式求解得

u=R2（i+is-αi）+R1（i+is）+us+R3i

整理得

u=us+（R1+R2）is+[R1+R3+（1-α）R2]i

此即为所求的一端口电路的伏安关系。

由于一端口电路的伏安关系与外接电路无关，因此，我们完全可以在最简单的外接电路情况下来求一端口电路的伏安关系。外施加电压源求电流法和外施加电流源求电压法是常用的方法，也是用实验方法确定一端口电路伏安关系的依据。

2.一端口电路的等效

在相同的端口电压和端口电流的参考方向下，如果两个一端口电路的外部特性完全相同，则称这两个一端口电路是相互等效的。对于一端口电阻电路来说，其外部特性就是指的端口的伏安关系。如图2-3中的N1和N2两个内部结构和参数均不相同的一端口电路，若两端口上的伏安关系（u～i关系）相同，则称N1和N2对端口u-i关系而言互为等效电路（Equivalent Circuit）。在保持端口上u～i关系不变的情况下，把电路N1变换成电路N2，或者把电路N2变换成电路N1，即称为电路的等效变换（Equivalent Transformation）。

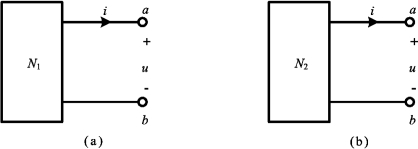
图2-3　等效电路的定义

应该注意的是：①两个一端口电路等效是指对任意的外部电路而言的，对内部电路并不等效，这就是说等效只是对外电路的等效，对电路内部不一定等效；②当任一电路的任一部分被等效变换后，该电路中其他部分的支路电压和支路电流并不因此变换而有所改变；③两个一端口电路的伏安关系是一种固有性质，与端口电压和电流参考方向的选取无关。

电路等效变换是电路理论研究的重要课题和成果之一，从研究的角度来看，是为了进一步研究更深层次的电路理论并获得更深层次的理论成果；从应用角度来看，是为了简化电路的分析计算，也就是为了分析和研究电路的方便，往往需要保持部分电路外部特性不变的情况下，将其内部电路进行适当的变化，用变化后的新电路结构代替被变化的部分电路，力求使得电路分析与计算更为简单和方便。这种通过等效变换来分析电路的方法称之为等效电路变换分析法（Equivalent Circuit Transformation Analysis）。