目前在人工地震勘探中应用的传感器主要有速度传感器和加速度传感器两种。最常用的是动圈磁电式速度传感器。另外，压电式加速度传感器、变容式微机电加速度传感器等新型传感器也可以应用。考虑到系统的实际使用要求，如传感器随弹丸抛撒后下落的姿态、系统成本及产品来源等，最常用的是以动圈磁电式速度传感器为系统的地震动传感器。动圈磁电式传感器是地震勘探中广泛使用的一种成熟传感器，其工作可靠、价格低廉，而且输出信号对后续电路要求不高，还可以简化系统电路设计。

一、磁电式速度传感器结构与工作原理

磁电式传感器是一种能把非电量（如机械能）的变化转换为感应电动势的传感器，又称为感应式传感器。根据电磁感应定律，ω匝线圈中的感应电动势e取决于穿过线圈的磁通的变化率，即

图13-3（a）和（b）是恒定磁阻磁电式传感器的结构原理图。

图13-3　恒定磁阻磁电式传感器结构原理图

（a）直线运动；（b）旋转运动

图13-3（a）为线圈作直线运动时的恒定磁阻磁电式传感器，它所产生的感应电动势e为

式中，Bd为气隙磁场的磁感应强度，单位T；l0为单匝线圈的有效长度，单位m；ωd为工作气隙中线圈绕组的有效匝数；V为线圈与磁场的相对运动速度，单位m/s；θ为线圈运动方向与磁场方向的夹角，单位rad。

当θ=90°时，式（13-2）可写成

图13-3（b）为线圈作旋转运动的恒定磁阻磁电式传感器。线圈在磁场中旋转时产生的感应电动势e为

式中，ω表示角频率，，单位rad/s；A为单匝线圈的截面积，单位m2；θ为线圈法线方向与磁场之间的夹角，单位rad。

当θ=90°时，式（13-4）可写成

由式（13-2）、式（13-4）可见，当传感器结构一定时，Bd、A、ωd、l0均为常数，因此感应电动势e与线圈对磁场的相对运动速度dx/dt（或dθ/dt）成正比，所以这种传感器的基型是一种速度传感器，能直接测量出线速度或角速度。但由于速度与位移之间存在积分关系，与加速度之间存在微分关系，只要在感应电动势的测量电路中加上积分或微分环节，磁电式传感器就可以用来测量运动的位移或加速度。

图13-3中的两种磁电式传感器均属于恒定磁阻式结构。从图13-3可见，磁路系统的空气气隙不变，故气隙磁阻也固定不变。图13-4为二极式变磁通（变磁阻）磁电式传感器。它的线圈和永久磁铁均不动，当椭圆形铁芯作等速旋转时，空气气隙时而变小，时而变大，使磁路系统的磁阻产生周期性变化，引起磁通相应变化，达到产生感应电动势的目的。

图13-4　二极式变磁通磁电式传感器

恒定磁阻磁电式传感器的基本部件有两个：一是磁路系统，由它产生恒定的直流磁场，为了减小传感器的体积，一般都采用永久磁铁；另一个是线圈，它与磁场中的磁通链产生感应电势。如前所述，感应电动势e与线圈对磁场的相对运动速度成正比，故二者之间必存在相对运动。其运动部件可以是线圈，也可以是永久磁铁。前者称为动圈式，后者称为动铁式。它们共属于线圈磁铁活动型。

线圈磁铁活动型磁电式传感器具体结构可分成相对式和惯性式两大类。

图13-5为相对式磁电式速度传感器的结构原理图。传感器的钢制圆筒形外壳1和与其紧密配合的空心圆柱形高磁能磁钢3组成磁路。信号线圈2位于磁路的环形空隙中。线圈骨架由非导磁材料或非金属材料制成，为了减小骨架中产生的涡流，若采用金属骨架其上常开有纵向槽。线圈骨架与连杆4的一端相连，连杆穿过磁钢，另一端与测量杆6相连。连杆4的两端由一对拱形簧片5支撑和导向，保证线圈在运动时与气隙始终同心。测量杆6也由拱形簧片支撑，其一端伸出壳体外，感受被测振动。测量杆中装有限位块，以免被测振幅过大时损坏测量杆。测量时，传感器外壳由人拿住或固定在参考静止点上，测量杆压在被测振动对象上。若测量杆始终与被测振动对象保持接触，则线圈便与被测振动对象作相同的运动，由线圈切割磁力线所产生的感应电动势e为

图13-5　相对式磁电式速度传感器的结构原理图

1—外壳；2—线圈；3—磁钢；4—连杆；5—簧片；6—测量杆

对于确定结构，Bd、ωd、l0均为常数，因此e与线圈对磁场的相对运动速度V成正比，传感器的灵敏度K为

式中，K的单位为V·s/m。

二、磁电式惯性传感器的振动特性

根据惯性式测量原理构成的磁电式传感器是一种测量机械振动的拾振器。它可以直接安装在振动体上进行测量，而不需要一个静止的参考基准（如大地）。因此，在运动体（如飞机、车厢等）的振动测量中有其特殊地位。这里着重讨论这种磁电式传感器。(www.daowen.com)

这种磁电式传感器由永久磁铁（磁钢）、线圈、弹簧、液体阻尼器和壳体等组成，如图13-6所示。

它是一个典型的二阶系统传感器。因此，可以用一个由集中质量m、集中弹簧k和集中阻尼c组成的机械系统来表示该二阶系统，如图13-7所示。对照图13-6和图13-7，永久磁铁相当于二阶系统中的质量块m，而二阶系统中的阻尼c大多由金属线圈骨架在磁场中运动产生电磁阻尼提供，当然也有的传感器还兼有空气阻尼器。

图13-6　磁电式惯性传感器的结构示意图

1—永久磁铁；2—线圈；3—弹簧；4—壳体；5—液体阻尼器

图13-7　二阶系统

在测量振动体的机械振动时，传感器壳体刚性固定在振动体上，传感器壳体跟随振动体一起振动。假如传感器的质量m较大，而弹簧较软（弹簧系数k较小），当振动体的振动频率足够高时，可以看作质量块的振动很大，来不及跟随振动体一起振动，以致接近静止不动。这种情况下，振动能量几乎全被弹簧吸收，而弹簧的伸缩量接近振动体的振幅。

为了求得惯性传感器性能的定量指标，分析图13-7所示的二阶系统。

设x0为振动体的绝对位移，xm为质量块的绝对位移，则质量块与振动体（或传感器壳体）之间的相对位移xi为

由牛顿第二定律可得到

应用微分算符，则上式可改写为

由式（13-11）可以求出相对输入x0的输出xm，若求其传递函数，则有

式中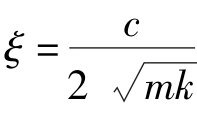，为相对阻尼系数（或称阻尼比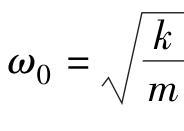）；为固有角频率。

由于测量的是动态物理量（如机械振动），因此传感器的频率响应特性是我们最关心的。若振动体作简谐振动时，亦即当输入信号x0为正弦波时，只要将D=jω代入式（13-

12），可得到频率传递函数的形式为

其振幅比为

相位为

将式（13-14）、式（13-15）用图表示，可得图13-8所示幅频特性。由图13-8可见，当ω≫ω0时，则振幅比接近1，且相位滞后180°，也就是说，若振动体的频率比传感器的固有频率高得多时，质量块与振动体之间的相对位移xi就接近于振动体的绝对位移x0。因此在这种情况下，传感器的质量块m可以看作静止的，即相当于一个静止的基准。磁电式传感器就是基于上述原理测量振动的。

仍以图13-6所示的磁电式惯性传感器为例。由于线圈与传感器的壳体固定在一起，而永久磁铁通过柔软的弹簧与壳体相连，因此当振动体的频率远高于传感器的固有频率时，永久磁铁就接近静止不动，而线圈则跟随振动体一起振动。这样，永久磁铁与线圈之间的相对位移十分接近振动体的绝对位移，其相对运动速度就接近振动体的绝对速度。由式（13-7）可知，线圈绕组中的感应电动势e为

对于结构已经确定的传感器，灵敏度K=Bdl0ωd可看作一个常数，因此在理想情况下，传感器的输出电动势正比于振动速度（见图13-9中虚线），但传感器的实际输出特性并非完全线性，而是一条偏离理想直线的曲线（见图13-9中实线）。偏离的主要原因是当振动速度很小时（小于υA），振动频率一定情况下，振动加速度很小，以致所产生的惯性力不足以克服传感器活动部件的静摩擦力，因此线圈与永久磁铁之间不存在相对运动，当然传感器也不会有电压信号输出。随着振动速度的增大（超过υA至接近υg），这时由于惯性力增大，克服了静摩擦力，线圈与永久磁铁之间已有相对运动，传感器也就有了输出，但由于摩擦阻尼的作用，使输出特性呈非线性。随着振动速度继续增大（超过υg至接近υc），这时与速度成正比的黏性阻尼大于摩擦阻尼，其结果使输出特性的线性度达到最佳。当振动速度超过υc以后，由于惯性力太大，以致传感器的弹簧超过了它的弹性范围，这时作用在弹簧上的力与弹簧变形量不再呈线性关系，因此使输出电压出现饱和现象。

由上述分析可知，传感器的输出特性在小速度和大速度范围之内是非线性的，而在实际工作范围内，其线性度是令人满意的。

图13-8　幅频特性

图13-9　电动式传感器的输出