一、基本算法

设4个传声器（M1、M2、M3、M4）构成边长为l的平面方阵，分别对称分布在xOy平面的4个象限，如图12-7所示。目标位于S（x，y，z），方位角为φ，仰角为θ，且OS=r，SM1=r1，M2M1=d21，M3M1=d31，M4M1=d41，则有

图12-7　空间定位原理图

这是一个未知数为x、y、z、r、r1的五元二次方程，求解该方程就可求得目标的位置S（x，y，z）。将方程组（12-39）中式③、④、⑤分别与式②相减，并解线性方程组，得到

为了实用，可在不影响精度的前提下对方程组（12-40）进行简化。由于r≫l，r1≈r，所以近似有

二、精度分析

方程组（12-41）中的式②、式③分别对d21、d41求偏导，有

并考虑声程差

根据误差合成理论，方位角φ和仰角θ的定向均方误差分别为

其中，σd为声程差d21、d41的均方误差。因此，空间定向的角度均方误差为

将方程组（12-41）中式①分别对d21、d31、d41求偏导，有

并考虑声程差(www.daowen.com)

可得距离r估计的均方误差

三、算法的改进

虽然平面四元方阵只有3个独立时延，但可估计的时延共有6个。对于定位计算来说，另外3个为非独立的冗余时延。充分利用d21、d34、d41、d32、d31和d42这6个时延，可提高定向和定距的精度。

在方程组（12-41）的定向公式②、③中，d32、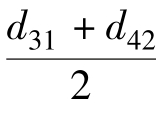与d41是等价的，同样d34、与d21是等价的，因此，令

可得方位角φ

仰角θ

根据方程组（12-41）的式①，同理可由d21、d42、d32求得r2，由d34、d31、d32求得r3，由d34、d31、d32求得r4。由于它们都是距离r的近似，且有对称关系，取其平均，并作技术处理，有

虽然式（12-47）～式（12-49）不是精确公式，但其引起的系统误差要比方程组（12-41）小得多，完全可以忽略。

式（12-47）、式（12-48）的方位角φ、仰角θ的定向均方误差和空间定向的角度均方误差分别为

同平面三元阵相比随机误差降到原来的一半。一般气象和干扰条件下，定向精度能满足技战术指标要求，但式（12-49）的定距随机误差为

同式（12-41）相比，式（12-51）引起的定距随机误差要小，并且通过卡尔曼滤波等后置数值处理方法还可提高定距精度，但也难以满足技战术要求。