一、基尔霍夫定律

任何物体都不断吸收和发出辐射功率。当物体从周围吸收的功率恰好等于由于自身辐射而减小的功率时，便达到热平衡。于是，辐射体可以用一个确定的温度T来描述。

1859年，基尔霍夫根据热平衡原理导出了关于热转换的基尔霍夫定律。这个定律指出：在热平衡条件下，所有物体在给定温度下，对某一波长来说，物体的发射本领和吸收本领的比值与物体自身的性质无关，它对于一切物体都是恒量的。即使辐出度M（λ，T）和吸收比α（λ，T）随物体不同且都改变很大，但两者的比值对所有物体来说，都是波长和温度的普适函数，即

各种物体对外来辐射的吸收以及它本身向外的辐射都不相同。现定义吸收比为零的物体为绝对黑体。换言之，绝对黑体是能够在任何温度下，全部吸收任何波长的入射辐射的物体。在自然界中，理想的黑体是没有的，吸收比总是小于1。

二、普朗克公式

19世纪末期，经典物理学遇到了原则性困难，为了克服此困难，普朗克根据他自己提出的微观粒子能量不连续的假说，导出了描述黑体辐射光谱分布的普朗克公式，即黑体的光谱辐出度为

式中，c1=2πhc2为第一辐射常数；c2=hc/k为第二辐射常数；h为普朗克常数；k为玻耳兹曼常数。

在研究目标辐射特性时，为了便于计算，通常把普朗克公式变成简化形式，即令和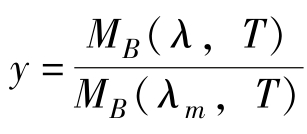，其中MB（λm，T）表示黑体的最大辐出度。

于是普朗克公式可表示为如下简化形式：

普朗克公式代表了黑体辐射的普遍规律，其他一些黑体辐射定律可由它导出。例如，将普朗克公式从零到无穷大的波长范围进行积分，就得到斯忒藩-玻耳兹曼定律；对普朗克公式进行微分，求出极大值，就可获得维恩位移定律。

实际应用中，普朗克公式也具有指导作用。例如，根据它的计算用来选择光源和加热元件，预示白炽灯的光输出、核反应堆的热耗散、太阳辐射的能量以及恒星的温度筹。(www.daowen.com)

三、维恩位移定律

普朗克公式表明，当提高黑体温度时，辐射谱峰值向短波方向移动。维恩位移定律则以简单形式给出这种变化的定量关系，即对于一定的温度，绝对黑体的光谱辐射度有一个极大值，相应于这个极大值的波长用λm表示。黑体温度T与λm之间有下列关系式：

式中，b≈2 897 μm·K。

维恩位移定律表明，黑体光谱辐出度峰值对应的波长λm与黑体的绝对温度T成反比。因此，根据被测目标的温度，利用维恩位移定律可以选择红外系统的工作波段。

一般强辐射体有50％以上的辐射能集中在峰值波长附近，因此，2 000 K以上的灼热金属，其辐射能大部分集中在3 μm以下的近红外区或可见光区。人体皮肤的辐射波长范围主要在2.5～15 μm，其峰值波长在9.5 μm处，其中8～14 μm波段的辐射能占人体总辐射能的46％，因此医用热像仪选择在8～14 μm波段上工作，便能接收人体辐射的基本部分能量。温度低于300 K的室温物体，有75％的辐射能集中在10 μm以上的红外区。

四、斯忒藩-玻耳兹曼定律

1879年，斯忒藩通过试验得出：黑体辐射的总能量与波长无关，仅与绝对温度的四次方成正比。1884年，玻耳兹曼把热力学和麦克斯韦电磁理论综合起来，从理论上证明了斯忒藩的结论是正确的，从而建立了斯忒藩-玻耳兹曼定律，即

式中，σ=5.67×10-8W/（m2·K4），称为斯忒藩-玻耳兹曼常数。

由斯忒藩-玻耳兹曼定律可知：当黑体温度有很小的变化时，就会引起辐出度的很大变化。例如，若黑体表面温度增高一倍，其在单位面积上单位时间内的总辐射能将增大16倍。

利用斯忒藩-玻耳兹曼定律，容易计算黑体在单位时间内，从单位面积上向半球空间辐射的能量。例如，氢弹爆炸时，可产生高达3×107 K的温度，物体在此高温下，从1 cm2表面辐射出的能量将是它在室温下辐射出的能量的1020倍。