正弦波调频时，引信发射信号为

式中，ΔωM=2πΔFM。

目标回波信号为

混频器输出差频信号为

滤除2ω0高频分量后，有

式中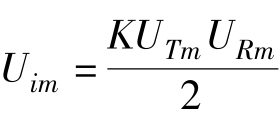，为差频信号幅值；K为混频器非线性偶次项系数。

应用关系为

式中，Jn为第一类n阶贝塞尔函数。

将式（5-92）展开，得到

式中各项最后一个括号内的τ/2值决定了所有谐波分量的初始相位，可以忽略。

由式（5-95）可见，混频器输出的差频信号的频谱与三角波线性调频差频信号的频谱相同，也是离散谱，且各次谐波是调制频率的整数倍，其n次谐波振幅为(www.daowen.com)

式中，λ为载波波长。

考虑到实际应用中，选择ΩM时，一般满足或τ≪TM，于是近似有

定义调制波长λM为

则式（5-97）可写为

由式（5-99）可见，n次谐波振幅Un与距离R的关系具有被n阶贝塞尔函数调制的正弦波形式。各次谐波振幅在距离R上的变化周期均等于λ/2，且各次谐波振幅受对应阶次的贝塞尔函数的幅度调制：

（1）各次谐波幅值的大小取决于弹目之间的距离，并且各次谐波振幅的最大值产生在各个不同的距离上。例如，一次谐波最大值对应的距离R≈0.17λM，二次谐波最大值对应的距离R≈0.26λM，三次谐波最大值对应的距离R≈0.34λM，四次谐波最大值对应的距离R≈0.44λM，15次谐波的最大值对应的距离R≈1.37λM，……。

（2）随着谐波次数的增大，各次谐波幅值（或最大值）也随之减小，即谐波次数越低，其信号能量（主要指信号幅度）越强。但各次谐波信号强度的变化不显著，因此单单依靠谐波能量大小区分各次谐波比较难以实现。

（3）就单次谐波而言，其幅值随距离R的减小而增大，但变化不剧烈，即正弦波调频的距离截止特性不太好。

（4）当距离R一定时，必然存在某一高次谐波n，高于此谐波的各次谐波在小于R的距离范围内其频谱均为零。例如，当R≤0.8λM时，15次及以上的谐波频谱强度都为零。