为分析方便，将锯齿波调频频率-时间曲线（图5-7）重新设置坐标，如图5-8所示，并将一个周期分成2个区间，区间1为规则区，区间2为不规则区。

图5-8　锯齿波调频信号频率随时间变化曲线（简化）

图5-8中发射信号fT（t）被提前了τ/2，接收信号fR（t）被延迟了τ/2。

发射信号的频率表示式为

接收信号的频率表示式为

已知φ=2π∫fdt，可以得到上述两式对应的瞬时相位差。分析如下：以一个周期作为讨论对象，分别先求出发射信号φF和接收信号φR的瞬时相位。

对发射信号，当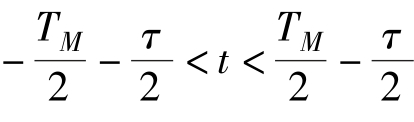时，

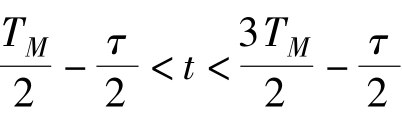当时，

式中，C为常数。

因为锯齿波调频的相位是连续的，即在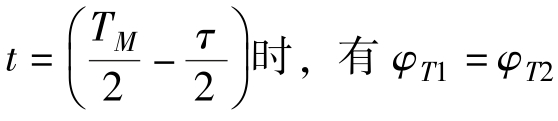。由此可得

对接收信号，当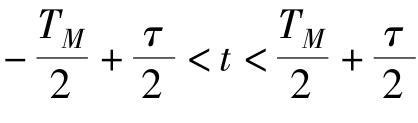时，则接收信号与发射信号的相位差为

当时，(www.daowen.com)

当时，

遇到目标后，返回的回波信号与发射信号（本振）相混频，得到的信号形式是cosΔφn，其展开形式为

计算傅里叶级数的系数，由于τ很小，不规则区部分对傅里叶级数系数的影响可以忽略，因此仅对规则区部分进行分析。

由式（5-70）可见，规则区部分两项分别被cos2πf0τ和sin2πf0τ加权，前半部分是偶函数，其傅里叶级数系数Bn为零；后半部分是奇函数，其傅里叶级数系数An为零。因此有

则An=ancos2πf0τ，Bn=bnsin2πf0τ，A0=a0cos2πf0τ，可得到规则区的傅里叶级数系数表达式为

式（5-78）加入了发射信号作为参考信号时的相位修正。因为延迟τ相对于调制周期很小，由差频展开式e可以看出，差频是离散的，差频的各次谐波系数是由发射频率、频偏、目标距离和调制频率共同决定的。

以上讨论的目标是静止的，当目标运动时，延迟τ不再是常量，此时，

不失一般性，令2πf0τ0=2kπ，则

相对运动时，差频的傅里叶级数转换为

其中，fa=（nfM＋fd），fb=（nfM-fd）。

与三角波线性调频类似，此时各次谐波处的谱线消失，取而代之的是与原来谐波相差±fd的两个谱线，相当于抑制载波的调幅。