三角波线性调频测距系统，其发射信号、目标回波信号和差频信号的时频曲线如图5-4所示，其中fT（t）表示发射信号频率，fR（t）表示接收信号频率（其中实线表示静止目标回波信号频率，虚线表示运动目标回波信号频率），f0表示载波频率，ΔFM表示调频频偏，TM表示调制信号周期，fi（t）表示差频频率（fi＋（t）和fi-（t）表示存在多普勒频移情况下的差频频率），τ=2R/c表示电磁波自引信到目标的往返时间，R为引信到目标的距离。

图5-4　三角波调频信号频率随时间变化曲线

假设线性调频波为理想三角波，忽略目标表面及传播媒介对发射、接收信号的影响，认为回波信号是发射信号经时间τ的延迟，则由图5-4可得，发射信号的瞬时频率表达式为

一、静止目标

对于静止目标，回波信号（图5-4中实线所示）频率为

于是差频信号频率为

从图5-4可知

将τ=2R/c和式（5-6）代入式（5-5），则得到差频频率fi（t）和距离R之间的关系为

或

对于一定距离R的目标回波信号，除去在t轴上很小一部分不规则区（对应一个调制周期TM内的极小时间τ=2R/c）以外，其他时间差频频率是不变的。若用频率计测量一个周期内的平均差频值fiav，可以得到(www.daowen.com)

实际工作中，应保证单值测距且满足

二、运动目标

对于运动目标，当目标与引信距离为R且径向速度为vR时，回波信号（图5-4中虚线所示）频率为

式中，fd为多普勒信号频率。

当fd＜fiav，即多普勒信号频率小于平均差频值时，得到差频信号频率为

可求出引信与目标之间的距离R为

用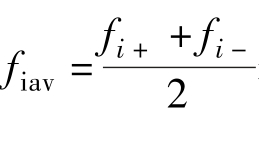表示一个周期内平均差频值，则有

式（5-12）和式（5-17）表明，当调制信号周期TM和发射信号的调频频偏ΔFM一定时，平均差频频率fiav和距离R成对应关系，只要测出平均差频频率fiav（仅次于fi的值），就可以得到距离R，这就是调频测距的基本原理。