对地面目标作用的自差式连续波多普勒体制无线电引信的炸高散布一般比较大。同样的射击条件下，由于地面性质不同，反射能力不同，炸高也不同。即使是在同样的地面情况下，炸高也有很大的散布。解决炸高散布、获取最佳炸高有各种不同的方法，其效果也不尽相同。这里介绍一种双支路信号处理获取准最佳炸高的方法。

将自差机检波输出的多普勒信号Ud分成两个支路进行处理，原理框图如图4-8所示。图4-8中A1、A2为放大器增益，τ为延时器延时时间，D为峰值检波器，U1、U2为多普勒信号的包络电压值。当U1、U2相等时，比较器输出点火脉冲。

图4-8　双支路信号处理获取最佳炸高原理框图

根据对地面目标作用时引信自差机检波输出的目标信号振幅随高度变化的关系式（4-36），两路输出分别为

当引信距地面高度为H时，第二支路由于延迟了τ秒，它的信号幅度对应于τ秒前引信所处高度上的振幅，即H＋τvdsinθ，其中τvdsinθ是τ秒内引信高度的变化量。

当U1=U2时，比较器输出点火脉冲信号，即可确定炸高H0。由式（4-48）和式（4-49）可得

令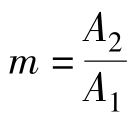，m＞1，则式（4-50）变为

式（4-51）为双支路信号处理电路的基本关系式。由此式可见，炸高与地面反射系数N无关，也不受引信高频参数及天线参数影响，仅与低频参数，如放大量A1、A2和延迟时间τ有关。

在实际应用时，根据引战配合要求，确定弹丸最佳炸高H与落角θ之间的函数关系为

将此函数关系代入式（4-51），得到(www.daowen.com)

式（4-52）说明，当给定落角θ时，为获得最佳炸高，τ与m的关系必须满足此式。在具体实现时，可以有两种方法。

1.m一定，改变τ

当m一定时，延迟时间τ由式（4-53）得

但直接测量落角θ和落速vd比较困难，可以通过多普勒频率与落角θ和落速vd的关系，通过测定多普勒频率来确定延迟时间，即将式（4-27）代入式（4-53），有

对榴弹而言，落速vd的变化为10％～20％，故可以取一个落速的平均值。显然，延迟时间τ与多普勒频率fd有一一对应关系。只要延迟时间τ满足式（4-55），便可在任意落角的情况下得到最佳炸高。

2.τ一定，改变m

当τ一定时，由式（4-55）得

显然，m与多普勒频率fd有一一对应关系。只要m满足式（4-56），便可在任意落角的情况下得到最佳炸高。

目前，采用单片机或DSP处理器技术很容易实现上述低频参数变化要求，由此可实现炸高稳定且不受地面性质影响的准最佳炸高方案。