一次射击杀伤单个目标，是一个复杂的随机事件，由随时间变化的两个独立随机事件组成。第一个随机事件是弹丸爆炸发生在相对于目标具有坐标（o，x，y，z）的空间给定点（x，y，z）。这一事件由炸点散布误差的分布密度函数Sd（x，y，z）确定。第二个随机事件是弹丸在给定炸点（x，y，z）爆炸时，杀伤单个目标的概率，用目标坐标毁伤概率pd（x，y，z）确定。严格地说，在空间某一点爆炸的概率实际上等于零。因此我们用接近（x，y，z）点处单元体积dxdydz内弹丸爆炸的概率表示，即用Sd（x，y，z）dxdydz表示。

根据概率乘法定理，单发弹丸在给定点（x，y，z）附近的单元体积dxdydz内爆炸时，毁伤目标的概率为

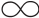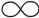由于炸点（x，y，z）是随机的，可能散布在很大的空间里，故一次射击毁伤单个目标的全概率p1（即单发毁伤概率）用一个区间由-到＋的三重积分表示：

将式（3-2）的坐标系转换为相对速度坐标系，如图3-7所示，这样在遭遇段战斗部相对目标做平行于xr轴的直线运动，战斗部的脱靶量ρ及脱靶方位θ在相对运动时保持不变，则单发毁伤概率可用相对速度坐标系中的圆柱坐标（ρ，θ，xr）来表示，此时，

式中，fd（ρ，θ）为引导误差随（ρ，θ）二维分布的分布密度函数；ff（xr/ρ，θ）为脱靶条件为（ρ，θ）时，引信启动点沿xr轴的分布密度函数；pf（ρ，θ）为脱靶条件为（ρ，θ）时，引信的启动概率。

图3-7　相对速度坐标系

于是，

令(www.daowen.com)

式中，pd（xr/ρ，θ）为炸点在（xr/ρ，θ）条件下战斗部爆炸时对目标的毁伤概率，即三维坐标毁伤概率。

则有

其中，pdf（ρ，θ）仅与ρ、θ坐标有关，称为二维目标毁伤概率，即通过脱靶平面上某一点（ρ，θ）的一条弹道上，对应引信起爆点的散布ff（xr/ρ，θ）所获得的条件坐标毁伤概率。它与ρ、θ的散布无关，故可作为评定引信与战斗部自身配合效率的指标。

由式（3-6）可看出，决定p1大小的主要是fd（ρ，θ）和pdf（ρ，θ）。fd（ρ，θ）由弹道散布误差决定，不是设计引信所能改变的，只能尽量实现获得最大pdf（ρ，θ）来加大p1。从式（3-5）又可看出，pdf（ρ，θ）的大小取决于ff（xr/ρ，θ）、pf（ρ，θ）和pd（xr/ρ，θ）；pd（xr/ρ，θ）和弹丸的性质以及弹目交会条件等有关，而与引信无直接关系；ff（xr/ρ，θ）和pf（ρ，θ）主要取决于引信本身的特性及引信起爆点散布的不同。

根据上述讨论可知，为了计算单发毁伤概率，必须：

（1）求获得最大pdf（ρ，θ）的分布函数ff（xr/ρ，θ）的散布中心；

（2）求坐标毁伤概率pd（xr/ρ，θ）。