1.水下抛填体稳定坡角

C值等于0的砂砾散粒土，水下自然休止角φp，比干抛休止角小1°～2°，可用下式表示

式中：D为相对密度；m为颗粒形状系数，均匀的圆粒砂为6～7，有角的砂砾为12。

风化砂有一定C值，如图6-7所示。

表6-5　风化砂干容重与抗剪强度参数关系

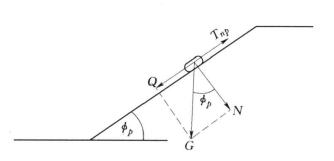
图6-7　有C值时，水下抛填体休止角φp

图6-8　承受施工荷载时，水下抛投体休止角φp

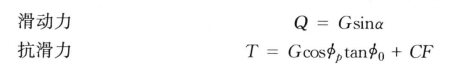
式中：F为滑动面面积；φ0为抛填体自由表面处摩擦角。

处于极限平衡状态时，Q=T，推得

有施工机械荷载p0（kPa）作用时，形成的水下抛投体边坡休止角φp，根据B.B索科洛夫斯基的研究（见图6-8），可用下式计算。(www.daowen.com)

式中：σ0=C/tanφ为粘性应力，kPa。

从上述公式看出，水下抛投风化砂实际形成的坡角，不仅与抛投料的物理力学性质有关，且与承受施工荷载大小与部位有关。当实际形成坡角陡于水下自然休止角（约27°），或承受外荷载突然加大时，均容易招致边坡滑塌。

2.水下抛投体极限填筑高度

如图6-9所示，滑动体重量G（kN）为

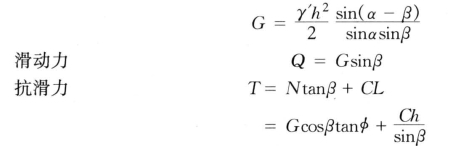
极限平衡时，Q=T，即可求得

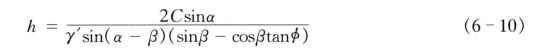
为了求出对应高度h的危险滑动面，令式（6-10）对β的导数为0，求得。表明水下抛投体危险滑动面将沿着边坡角α和填料内摩擦角φ之间的夹角等分线发生。

将β=代入式（6-10），水下抛投C取半值，得

表明当α＞φ时，与不同坡角相对应的水下抛投体极限填筑高度随C值大小而增减。当坡角α愈大时，极限坡高h愈小，由此可得出深水抛投形成的高填方自然稳定坡面为凹形面（图6-10）。

图6-9　水下抛填体极限填筑高度计算

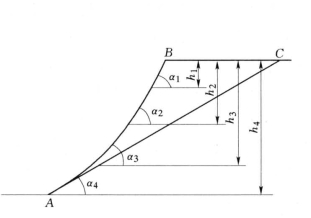
图6-10　水下抛投高填方的自然稳定坡面