（1）所用符号和代号的含义（见表13-70）

表13-70 符号和代号的含义和单位（SJ/T 2923—1988）

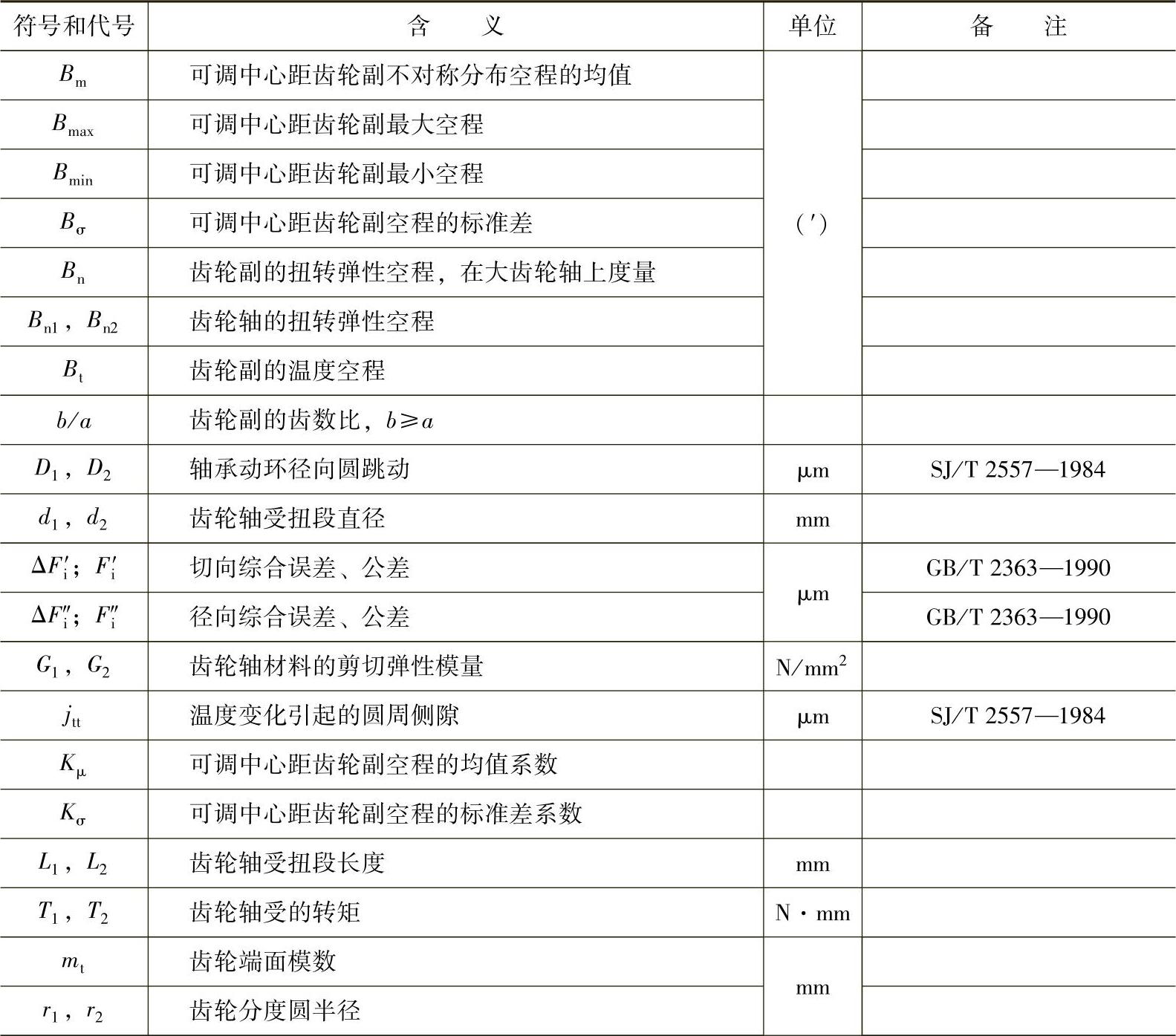
（续）

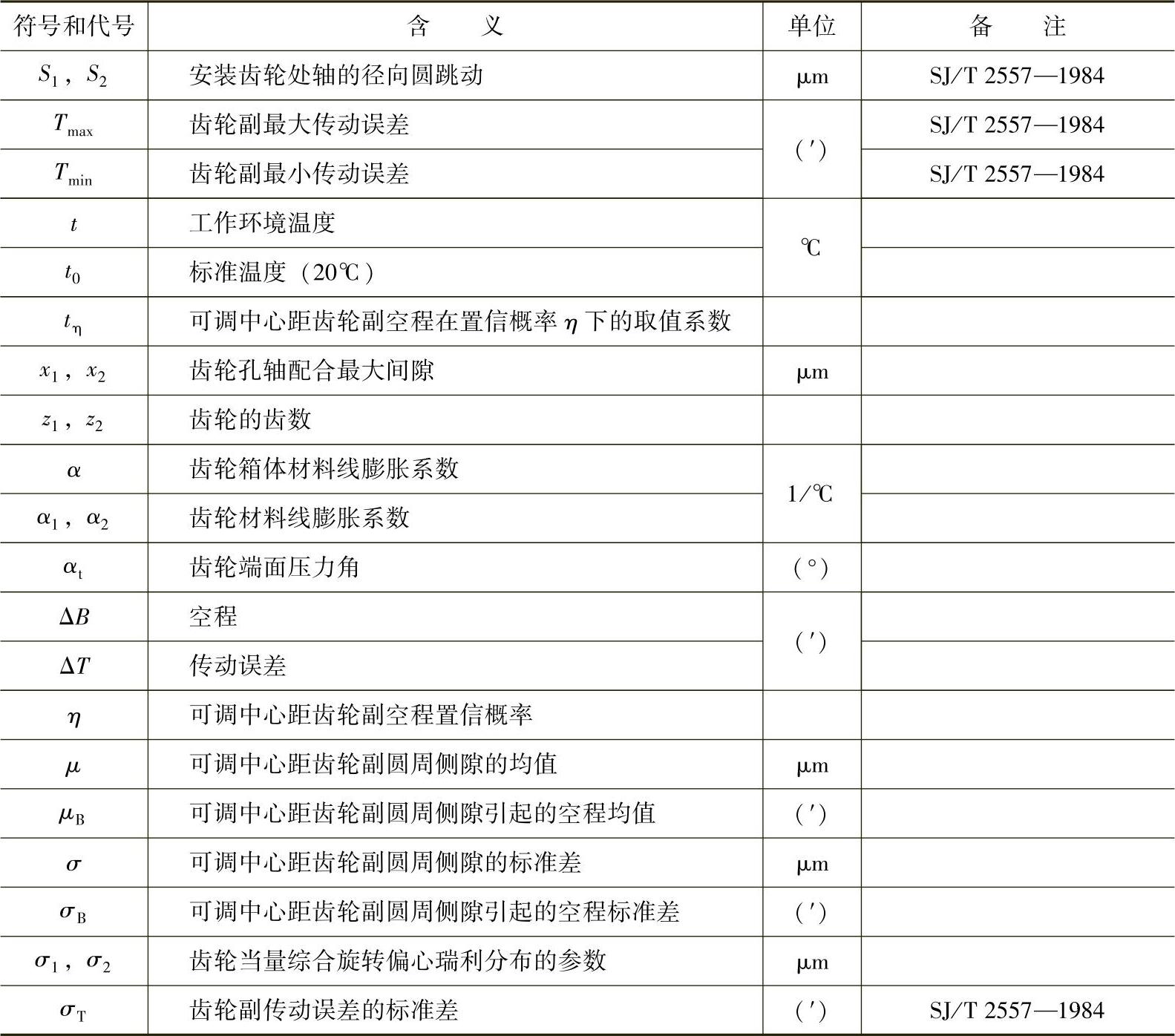
注：脚注1、2分别为齿轮副的小齿轮、大齿轮或小齿轮轴、大齿轮轴。

（2）空程计算

折算到齿轮副大齿轮轴上的最大、最小空程、空程的均值和标准差分别为

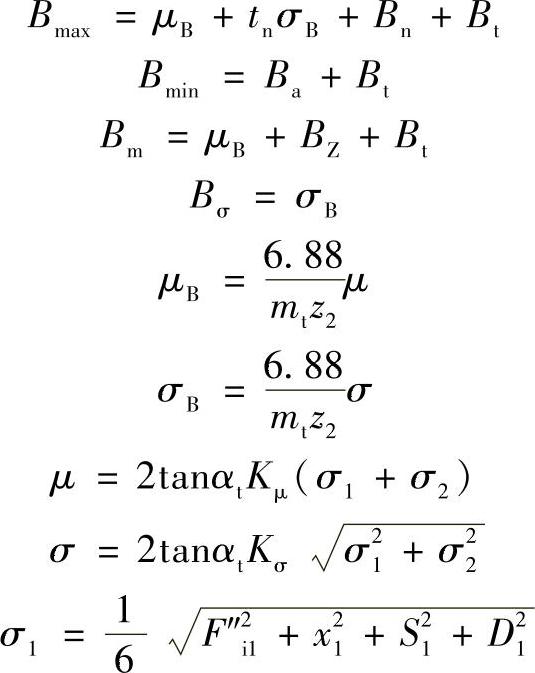
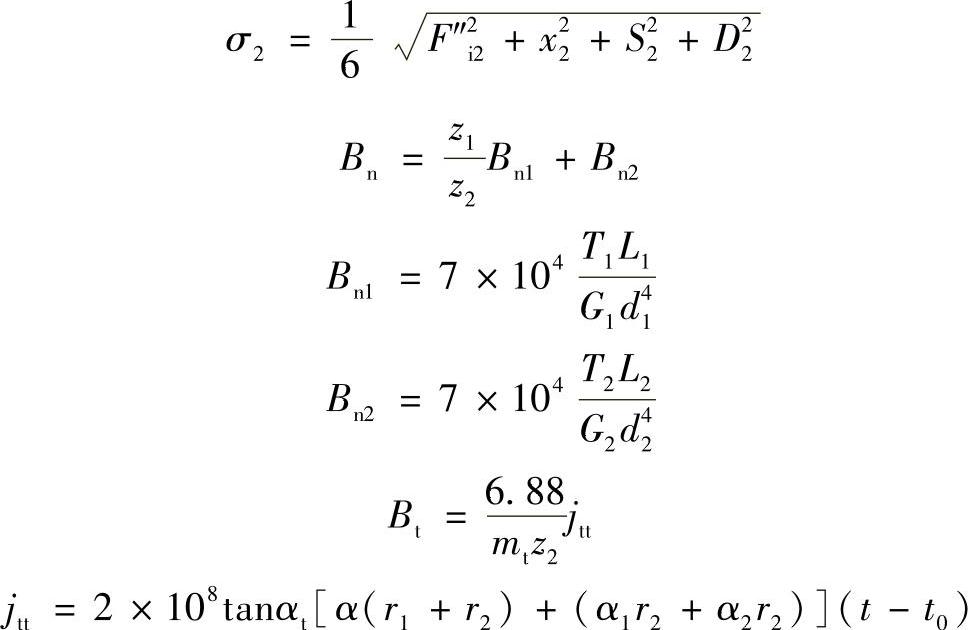
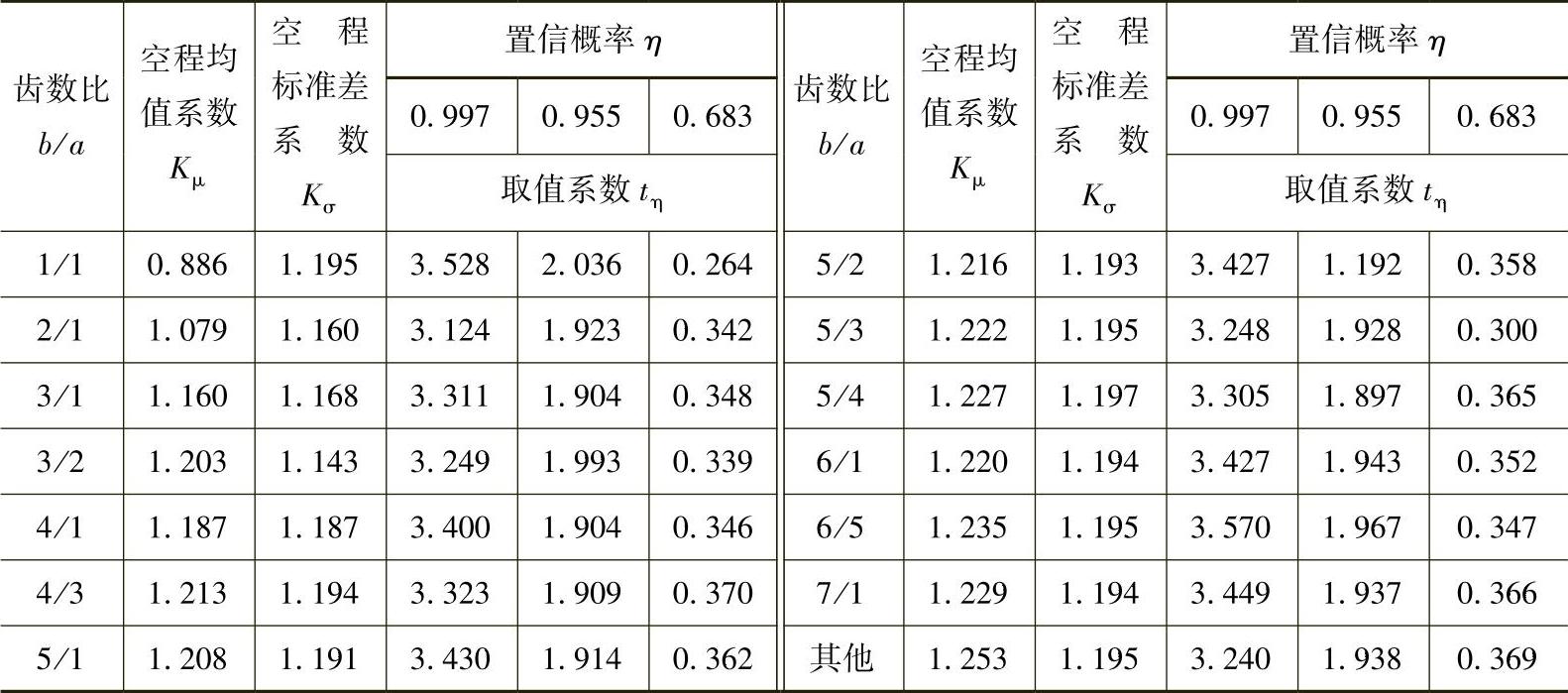
K_μ、Kσ、t_η由表13-71查取。

表13 - 71 K_μ、Kσ、K_η值（SJ/T 2923—1988）

（3）传动误差计算

折算到齿轮副大齿轮轴上的最大、最小传动误差分别为

T_max=3σ_T

T_min=-3σ_T

式中

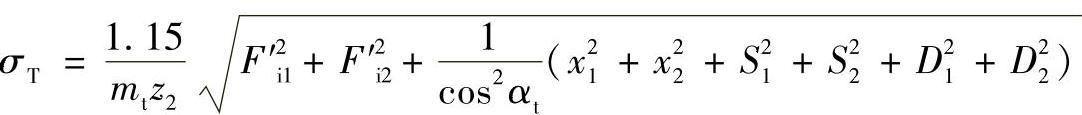
（4）空程及传动误差计算实例

例13 - 1 确定下列各可调中心距齿轮副的齿数比、空程的均值系数、空程的标准差系数、空程置信概率为0.997时的取值系数。

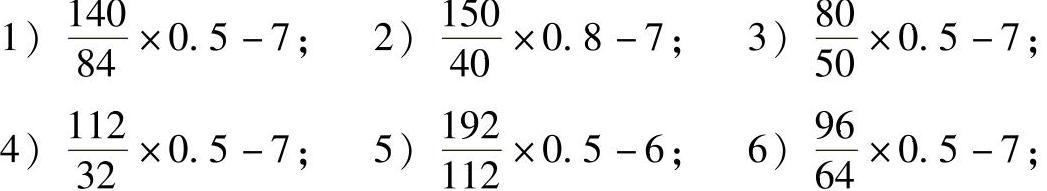
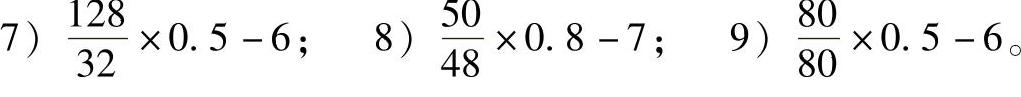(www.daowen.com)

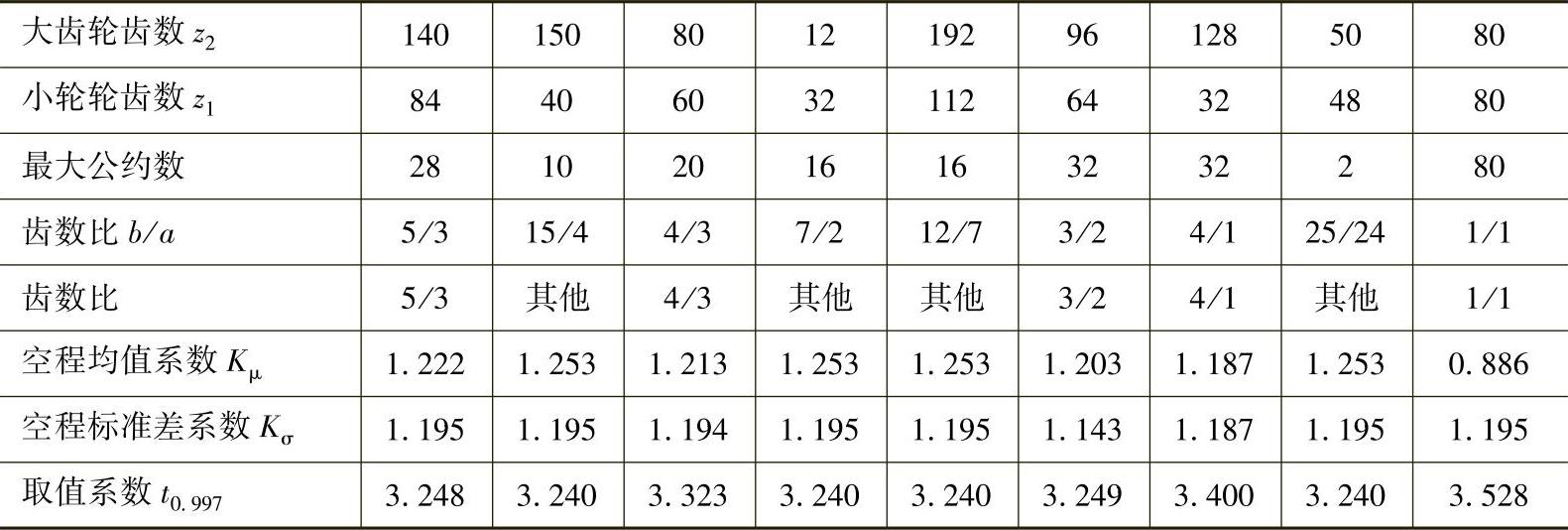
解：对各可调中心距齿轮副分别列出大齿轮齿数、小齿轮齿数，并求出其最大公约数及轮副的齿数比，按求出的齿数比在表13-71中查取相应的空程均值系数、空程标准差系数、指定置信概率下的取值系数，并记录在表13-72中。

表13 - 72 例13-1计算结果

例13 - 2 计算例13-1中可调中心距齿轮副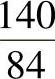×0.5-7的空程和传动误差。已知：齿轮孔轴配合最大间隙x₁=x₂=20μm；安装齿轮处轴的径向圆跳动S₁=S₂=10μm；轴承动环径向圆跳动D₁=D₂=10μm。

解：由GB/T 2363—1990查得：F′_i1=41μm；F′_i2=44μm；F″_i1=37μm；F″_i2=39μm；由例13-1已知：K_μ=1.222；Kσ=1.195；t_0.997=3.248；根据前述公式求出齿轮当量综合旋转偏心瑞利分布的参数，齿轮副圆周侧隙均值、标准差及其所引起的空程均值的标准差，最后求得可调中心距齿轮副最大、最小空程和空程的均值与标准差（根据已知条件，本题对空程的计算不必考虑扭转弹性空程和温度空程）：

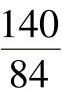
根据前述公式求得齿轮副传动误差的标准差和最大、最小传动误差：

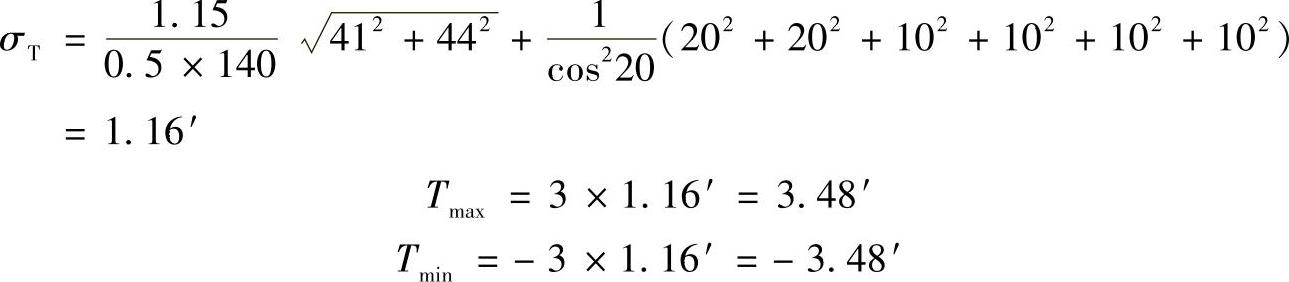
（4）可调中心距齿轮副空程的均值系数、标准差系数和取值系数计算径向齿隙Δ′（t）为一随机过程：

Δ′（t）=Δ（t）+Δp

式中，变值径向齿隙Δ（t）=ρ₁sinΦ₁+ρ₂sinΦ₂；Δp是Δ（t）负峰值的绝对值；ρ₁、ρ₂分别服从以σ₁、σ₂为参数的瑞利分布；Φ₁=Φ₀₁+ω₁t，Φ₂=Φ₀₂+ω₂t，Φ₀₁，Φ₀₂在[0，2π]上服从均匀分布。

引进含齿数比的线性变换后，可以证明以齿数2转角度量的Δ（t）的相位Θ和两旋转偏心矢量间的初始相位差Φ，分别服从均匀分布和梯形分布，并且它们不相互独立。也可以证明，Δ′（t）是广义平稳随机过程，其均值与方差分别为

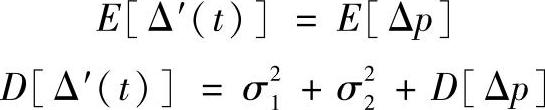
而

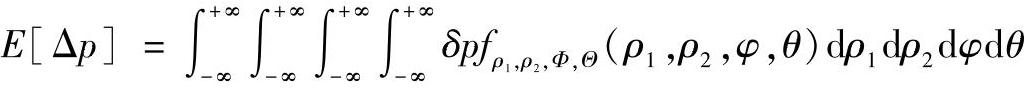
式中，δp为Δp的取值。经推导可得：

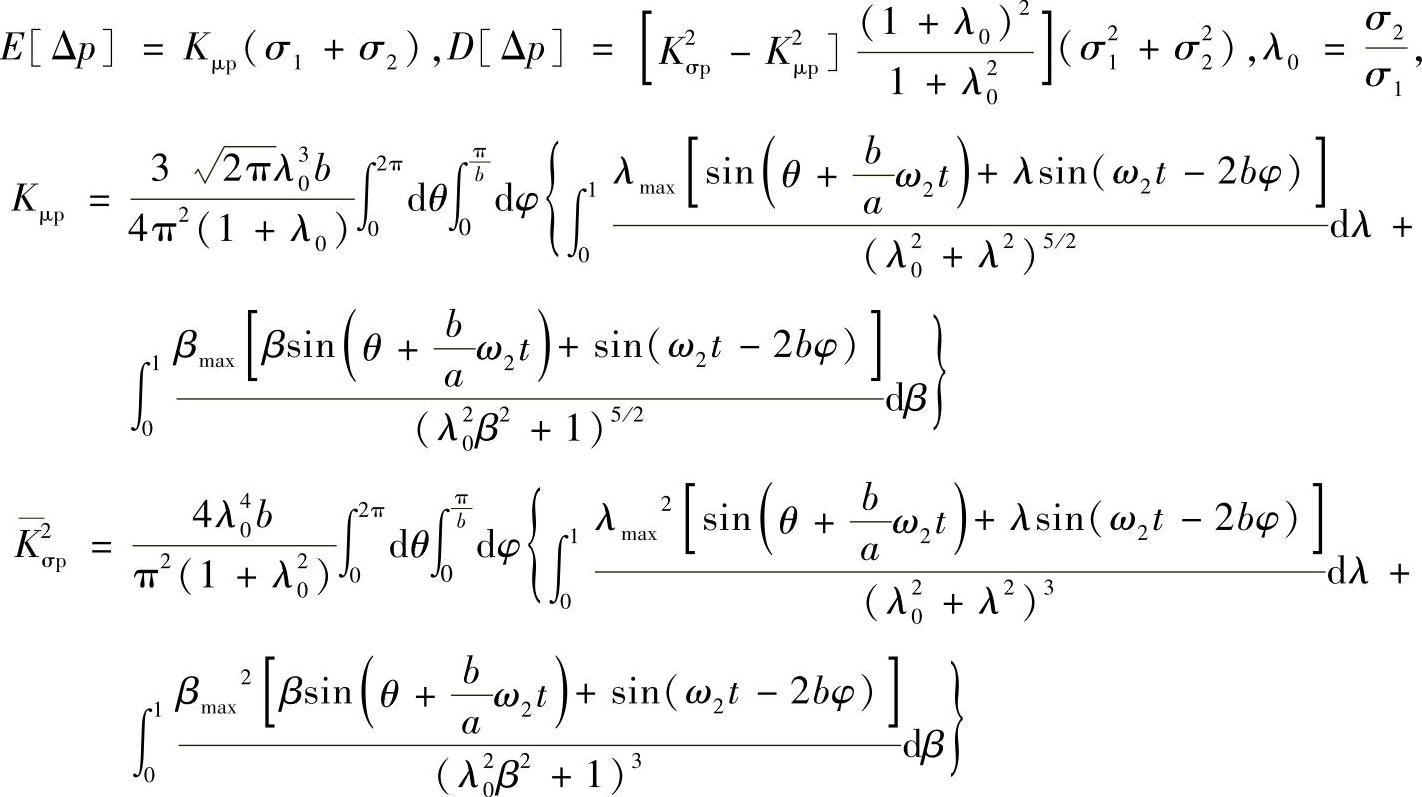
令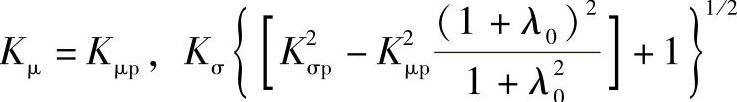，且由上述相应公式得：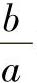

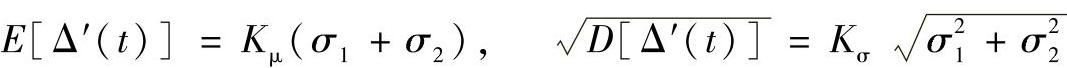
式中，K_μ、Kσ则为空程均值系数和空程标准差系数。它们分别由数值积分在计算机上求出。

因为Δ′（t）的一维概率分布无法用显式表出，故用统计模拟法模拟Δ′（t）的概率分布。在置信概率_η下，求得取值系数t_η。