机器人用RV传动必须具有高的运动精度和小的回差外，还必须具有很高的刚度。这也是它与谐波传动相比，在机器人传动中最突出的优点之一。RV传动的低速级是采用多齿啮合的摆线针轮传动，其接触刚度之高是众所周知的。高速级则采用有3个行星轮的渐开线行星齿轮传动，不仅提高了承载能力，同时也提高了刚度。除此之外，输出机构为刚架结构的行星架，也具有很高的刚度。机器人用RV传动对扭转刚度有严格的要求，通常在额定转矩下，由扭转弹性变形引起的弹性回差不超过4′～5′。

1）采用常规的力学方法对RV传动的每个组成部分进行刚度分析计算

①摆线针轮传动部分的弹性变形。摆线针轮传动部分的变形主要由针齿与摆线轮齿的接触变形及针齿与针齿壳上针齿孔的接触变形两部分组成。

由（2）的受力分析理论，可以得出在额定转矩的作用下，针齿与摆线轮及针齿壳这两部分的总接触变形的最大数值w_max，由此，假定摆线轮固定时，由于此接触变形而引起针轮产生的转角为

式中 r′_p——针轮节圆半径。

将针轮弹性转角折算到输出轴上，可得当固定渐开线中心轮时，由于针齿与摆线轮齿的接触变形及针齿与针齿壳的接触变形所引起的输出轴的转角Δθ_c为

Δθ_c=Δθ_pi¹₆₅ （11-139）

式中 i¹₆₅——当渐开线中心轮固定时，输出轴相对于针轮的传动比，即

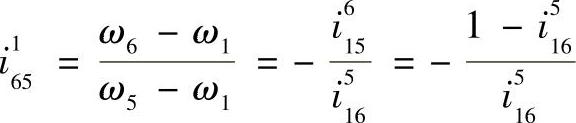
②渐开线传动部分的弹性变形 按照ISO刚度计算方法，首先计算单齿刚度，然后根据单齿刚度计算其啮合刚度。对于刚性啮合齿轮，在中等载荷作用下，其单对齿刚度按下式近似计算：

式中 q——单位齿宽柔度（mm·μm/N）。

当x₁≥x₂，-0.5≤x₁+x₂≤2.0时，q按下式计算：

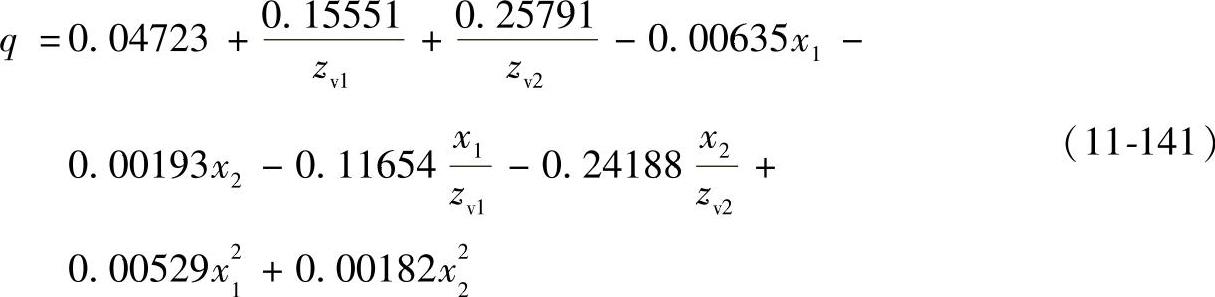
式中 x₁——小齿轮的变位系数；

x₂——大齿轮的变位系数；

z_v1——小齿轮的当量齿数，对直齿轮z_v1=z₁；

z_v2——大齿轮的当量齿数，对直齿轮z_v2=z₂。

根据ISO啮合刚度计算B法，考虑齿轮啮合时的重合度的影响，齿轮的啮合刚度为

c_r=（0.75ε_α+0.25）c′ （11-142）

式中 ε_α——端面重合度；

c′——单对齿刚度[N/（mm·μm）]。

根据刚度的定义，啮合点的位移为

式中 F_gt——中心轮受的啮合力的切向分力（N）；

b_g——渐开线齿轮宽度（mm）；

α′——渐开线齿轮的啮合角（°）。

由啮合点位移使中心轮产生的转角为

式中 r′₁——渐开线中心轮的节圆半径（mm）。

当固定针齿壳及中心轮时，由于渐开线齿轮传动部分的弹性变形而引起输出轴的转角为

式中 i⁵₁₆——当针轮固定时，输入轴相对于输出轴的传动比。

③行星架的弹性变形。行星架是由两块侧板1、2和三个截面近似梯形的连接柱销3组成。行星架的弹性变形是指在转矩T的作用下两块侧板的相对转角，如图11-61所示，它也可以表示为在半径为r_n圆周方向上由切向力F_nt引起的位移Δ的大小，而切向力

式中 F_G1t——曲柄作用在侧板上的切向力（N）；

r_n——连接柱销形心到行星架中心的距离（mm）；

a₀——曲柄支撑轴承中心到输出轴中心的距

离（mm），其数值等于渐开线行星齿轮传动中心距。

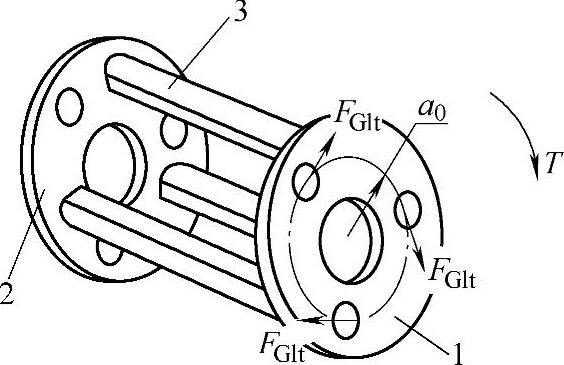
图11-61 行星架示意图

参照图11-62行星架展开图，切向位移量Δ可表示为

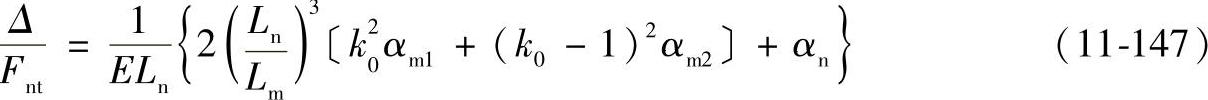
式中 α_m1——切向力F_nt对侧板1的弯曲变形和剪切变形的影响系数；

α_m2——切向力F_nt对侧板2的弯曲变形和剪切变形的影响系数；

α_n——切向力F_nt对连接柱销弯曲变形和剪切变形的影响系数；

k₀——两块侧板的刚度比较系数；

L_m——侧板1/3段的弧长（mm），；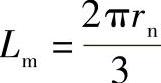

L_n——两块侧板中心平面间的距离（mm）；

E——弹性模量（MPa）。

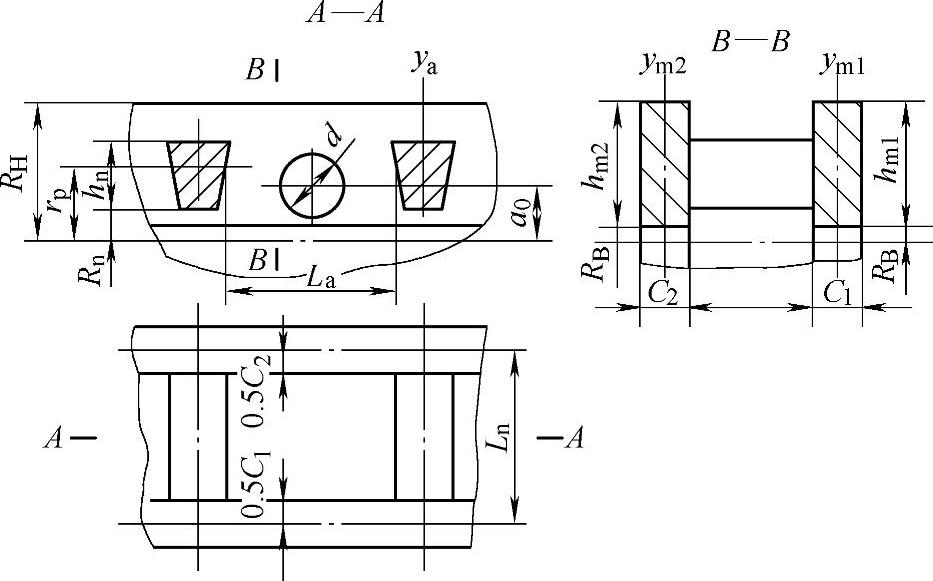
图11-62 行星架截面展开图

且

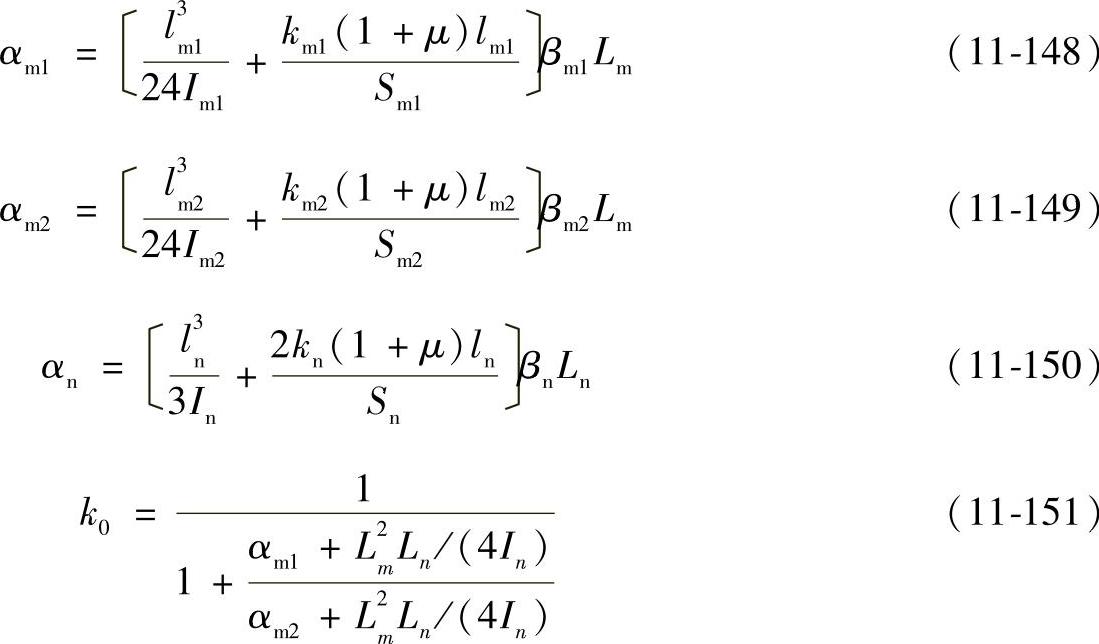
式中 β_mi——两圆盘形侧板的形状系数（i=1，2）；

β_n——凸四边形连接柱销的形状系数；

k_mi——两侧板的横截面形状系数（i=1，2）；

k_n——连接柱销的横截面形状系数；

I_mi——两侧板相对于y_m轴的截面惯性矩（i=1，2）（mm⁴）；

I_n——连接柱销对于y_n轴的截面惯性矩（mm⁴）；

S_mi——两侧板的横截面积（i=1，2）（mm²）；

S_n——连接柱销截面积（mm²）；

l_mi——相当悬臂变形的两侧板有效长度（i=1，2）（mm）；

l_n——相当悬臂变形的连接柱销件的有效长度（mm）；

μ——泊松比，μ=0.3。

式中系数由有关图表确定，惯性矩和面积是按照图11-62行星架展开图尺寸计算的。由此，可按式（11-147）计算出行星架两侧板相对位移Δ值，因此，由行星架弹性变形引起输出轴转角为

④曲柄轴的弹性变形。曲柄轴的周向弹性变形由曲柄轴的周向弯曲变形和扭转变形两部分组成，下面分别进行计算。

a.曲柄轴的周向弯曲变形。由本章11.2节关于传动曲柄及行星轮的受力分析，曲柄轴受两摆线轮在轴承孔分布圆周切向力的作用（参见图11-49），引起曲柄有此方向上的弯曲变形，从而导致输出轴产生一定的转角。根据材料力学梁的挠度计算方法，对于变截面的曲柄轴，为了提高计算精度，本文采用有限插分法计算挠度。在突变截面附近选择一些点增加差分点数，如图11-63所示，截面3和截面4处的位移即为所求挠度。

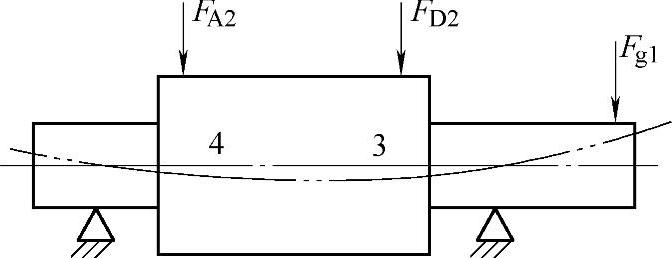
图11-63 曲柄受力变形图

这里，摆线轮给曲柄轴的圆周方向的作用力为

式中 T_c——一片摆线轮承受的转矩（N·mm）。

曲柄轴上的行星轮受到的切向力

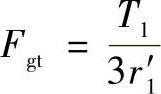
式中 T₁——输入的转矩（N·mm）。

由于曲柄在截面3和截面4处的位移不同，在计算曲柄变形引起输出轴转角时，应以它们的平均值f_m来计算

式中 f₃——截面3处的位移（mm）；

f₄——截面4处的位移（mm）。

由此，由曲柄轴的周向弯曲变形引起输出轴的转角为(www.daowen.com)

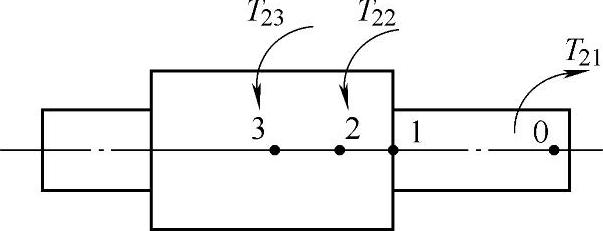
图11-64 曲柄受转矩作用图

b.曲柄的扭转变形。如图11-64所示，曲柄受转矩作用时，截面0与截面3之间将产生一定的相对转角ΔφS

式中 G——切变模量（MPa）；G=8×10⁴MPa；

T_2i——曲柄轴各段转矩（N·mm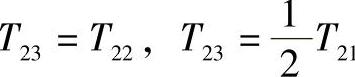），而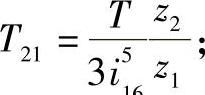

T——输出轴转矩（N·m）；

J_pi——极惯性矩（mm⁴），；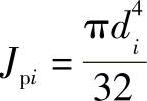

d_i——曲柄轴各段轴直径（mm）；

l_zi——曲柄各段轴长（mm）。

因此，由于曲柄的扭转变形产生的输出轴的转角

由式（11-155）及式（11-157）可得，由于曲柄的变形引起输出轴的转角为

Δθ_S=Δθ_S1+Δθ_S2 （11-158）

⑤轴承的弹性变形

a）轴承的变形与外载荷的关系 轴承内外圈与滚子接触处的总接触变形为

δ_z=k_zQ^0.9 （11-159）

式中 Q——滚子所受压力（N）；

k_z——刚度系数，k_z=7.66×10^-5/L^0.8；

L——滚子有效长度（mm）。

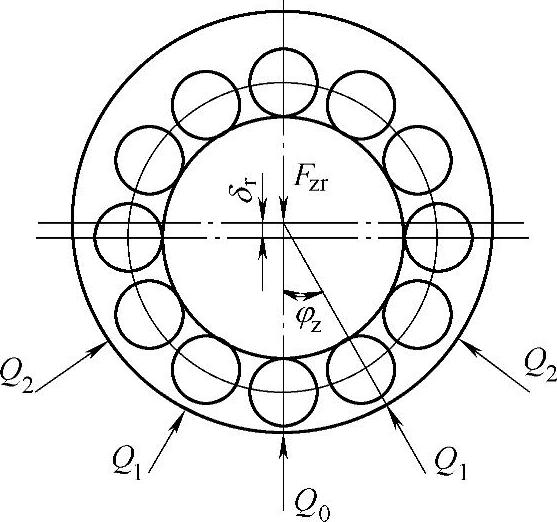
图11-65 轴承受力分析图

图11-65是轴承受径向力作用时的变形情况。在径向力F_zr作用下，轴承内外圈相对位移为δ_r，为计算方便将最下方的滚子的序号记作0，依次向上编为1，2，…，n等，相邻滚子所对圆心角为φ_z。在F_zr作用下，各个滚子的受力大小及变形量各不相同，序号为j的滚子受力为Q_j，与内外圈接触变形量的和为δ_j，设轴承游隙为Δr，则根据几何关系，有

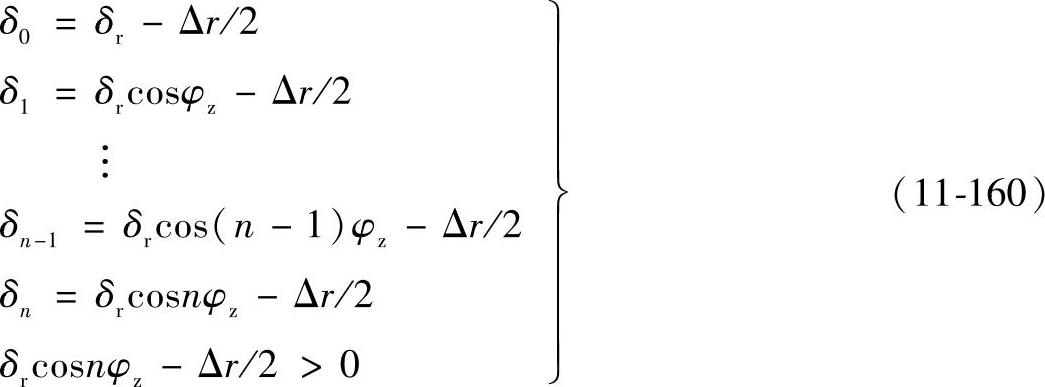
式（11-160）称为轴承弹性变形协调条件，由方程组中的不等式可确定受力滚子的最大序号n，n又称为分布系数，2nφ_z为轴承的负荷分布角。在圆心角2nφ_z范围内的滚子承受载荷，并产生接触变形。当轴承有预紧量时，Δr为负值，轴承的分布角大于π。除了预紧或游隙影响轴承的负荷分布外，外载荷也影响负荷的分布。在有游隙时，外载的增大会引起分布角的增加。相反，在有预紧量时，外载的增加引起负荷分布角的减小。将式（11-159）代入式（11-160）得

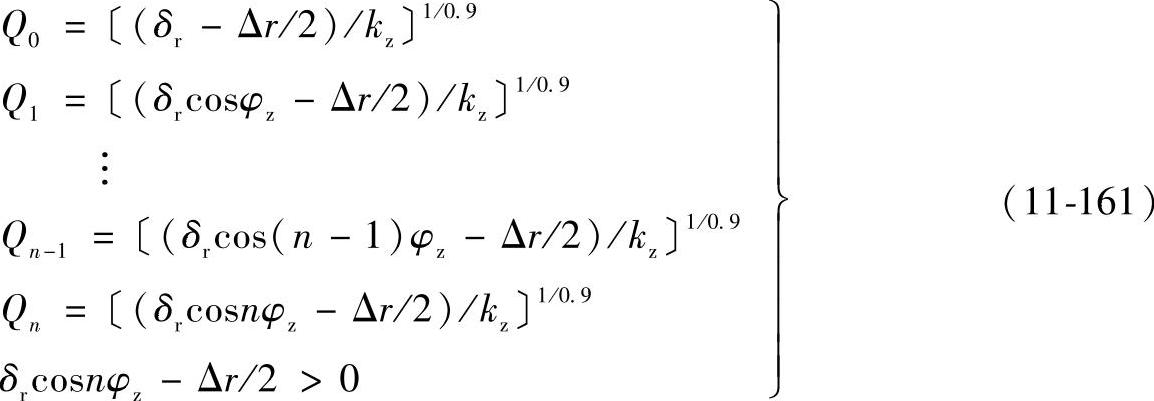
轴承不受外力作用时，各滚子受力一样，与内外圈作用的合力为0。当轴承受外力作用时，各滚子的受力情况发生变化，滚子与内圈作用的合力与外载达到新的平衡状态，其平衡条件为

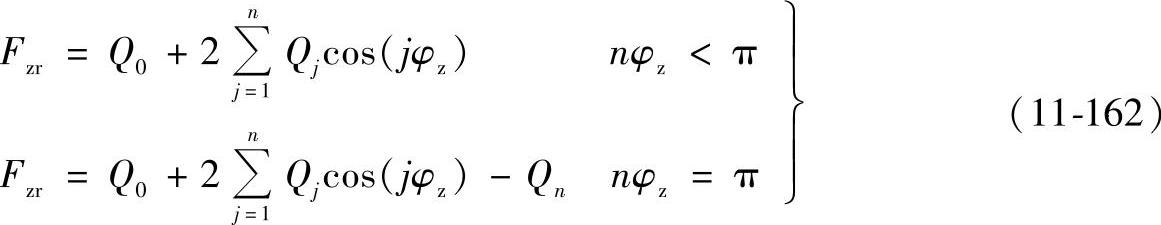
为了找出轴承内外圈的相对位移量与外载荷的关系，而位移量直接与内力大小有关，内力的大小又与外载、轴承结构、滚子及滚道的变形有关。因此，这种关系的计算不能直接套用公式，必须利用迭代的方式逐步逼近其真实解。

对于滚子轴承，先给出最大负载的初值

Q₀=4.6F_zr/z （11-163）

式中 F_zr——实际外载荷（N）；

z——滚子数量。

由式（11-159）计算出受载最大的滚子的变形量δ₀，由δ₀和游隙或预紧Δr根据变形协调条件求出相对位移量δ_r及各滚子的变形量δ_j和分布系数n。根据变形量δ_j和滚子负载Q_j的关系，可以求出每一个滚子的负载Q_j，再由平衡条件求出在假设滚子最大负荷Q₀的情况下的外载荷F_z′_r。由于在求初值Q₀时没有考虑实际游隙或预紧量，由此求出的载荷F′_zr与实际载荷F_zr不同，其误差用下式表示：

F′_zr-Fzr/F_zr＜ε （11-164）

式中 ε——收敛精度。

若精度不符合要求，需要进行下一轮迭代，按F′_zr-F_zr的大小修正Q₀的初值

Q^*₀=Q₀±F′_zr-Fzr/2 （11-165）

式中当F_z′_r＞F_zr时取负号，反之F_z′_r<F_zr时取正号。Q^*₀为新一轮迭代的初值。

曲柄支撑轴承为圆锥滚子轴承，目前尚缺乏有效的简易算法进行计算。我们仍利用分析圆柱滚子轴承的方法，对其变形及受力进行合理的变换。β_z为圆锥滚子轴线与轴承轴线之间的夹角，由于轴承轴向固定，所以在径向力F_zr作用下，其径向位移δ_j分为滚子轴向滑动位移δ_jt和法向位移δ_jn，其中的法向位移δ_jn=δ_i/cosβ_z是法向力Q_j产生的接触变形，由此外载在计算程序中应进行如下的相应变化

b.轴承变形引起输出轴的转角。根据轴承受力变形计算程序，可以算出曲柄支撑轴承及转臂轴承的内外圈相对位移量，从而求出轴承接触变形引起输出轴的转角。

曲柄支撑轴承周向变形引起输出轴的转角Δθ_b1计算如下：

固定摆线轮，在输出轴上加转矩T，则曲柄支撑轴承受到的圆周方向作用力为

式中 a₀——曲柄支撑轴承中心到输出轴中心的距离，其数值等于渐开线行星齿轮传动中心距。

采用上述计算程序，可计算出支撑轴承有转矩T的作用下内外圈产生的相对位移量δ_r1，则在轴承孔中心圆的周向上产生的转角为

转臂轴承周向变形引起输出轴的转角Δθ_b2计算如下：

由摆线轮承受的转矩T_c作用在转臂轴承上的周向力F_A2可以计算出，当固定输入轴、输出轴时，由转臂轴承变形引起摆线轮在半径为a₀的圆周上切向位移量δ_r2，则引起摆线轮的转角为

随摆线轮的转动，针轮产生相应的转角Δθ₅为

式中 i^H₄₅′——当输出轴、输入轴固定时，摆线轮相对于针轮的传动比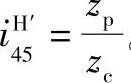。由此可得，当针轮固定时，由转臂轴承的变形引起输出轴的转角为

式中 i¹₆₅——当输入轴固定时，输出轴相对于针轮的传动比。

根据以上的分析，曲柄支撑轴承与转臂轴承的变形引起输出轴的转角为

Δθ_b=Δθ_b1+Δθ_b2 （11-172）

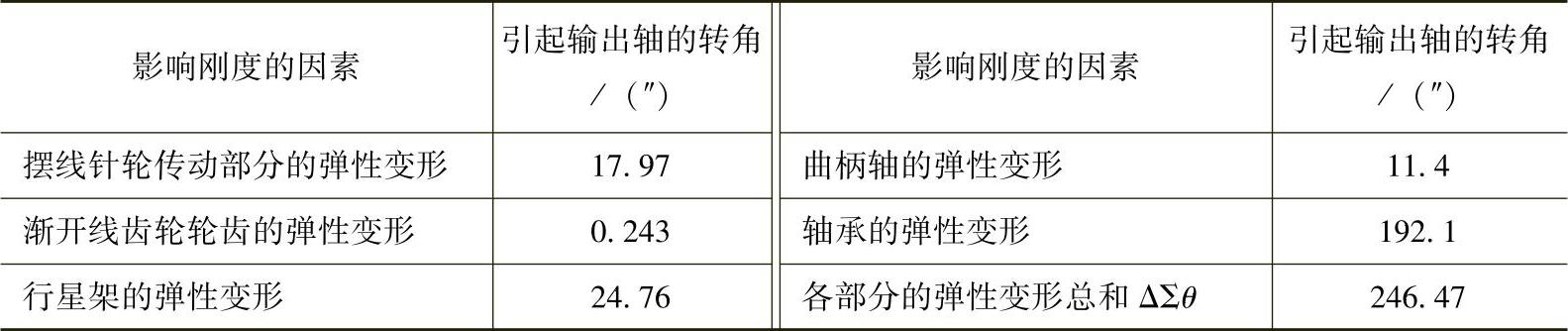
以机器人用RV-60AⅡ减速器为例，以上五种弹性变形引起的输出轴转角见表11-31。

表11-31 弹性变形引起输出轴的转角

然后可得RV-60AⅡ减速器的刚度k为

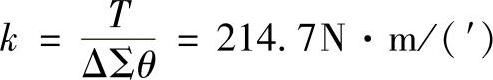
从计算结果看出，在额定转矩作用下，轴承的变形最大，刚度最小，正是基于这一实际情况，所以在本章11.2节中对RV传动整体受力分析时，以此为基础，假定摆线轮与曲柄轴刚度很大，而轴承可看成弹性体。从而总结出将RV传动受力的静不定问题简化成静定问题求解的力分析方法及公式。

由于轴承的刚度很小，难于提高，而机器人传动对RV减速器整体的抗扭刚度又有很高的要求，所以必须尽可能增大其他零件的刚度，以弥补轴承刚度的不足。主要措施是：①摆线轮齿形采用负移距与负等距组合修形，可以保证多齿啮合的共轭齿形，增大了摆线轮与针轮齿啮合的刚度；②针齿不用两支点而是用半埋齿以消除其弯曲变形；③输出轴采用刚性尽可能大的大直径圆盘输出。

2）整体刚度的有限元分析RV传动系统是由渐开线行星传动与摆线针轮行星传动组成的一个完整的封闭式差动机构体系，如果只把某个零件从机构中单独取出来进行有限元计算，那么，机构体系中几个重要计算对象之间的相互影响就很难准确地反映到计算模型中去，计算结果也将失去一些精度。为避免上述缺陷，在计算模型中应将摆线轮、行星架、偏心轴、针轮等同时纳入一块参与计算，这样才能使计算结果更加准确可靠，图11-66为RV传动结构系统的整体有限元计算模型。

传动中的摆线轮以自己的回转轴作平面圆周运动，这个回转运动是通过摆线轮内的偏心轴承实现的。轴承外环即为摆线轮内孔，它的网格划分沿环向是均匀的，在每一个接触点对上用“点对点”的接触单元模拟它们的弹性接触。对轴承滚柱以及内环，则将其凝聚到曲柄点上，用I-DEAS的刚性元及自由度释放技术，可以模拟轴承的“铰接”作用，从而实现了摆线轮与曲柄之间的铰接。

考虑到两片摆线轮是主要传递载荷零件，摆线轮齿部分网格划分密一些，可以真实地反映局部的应力与变形情况，两片摆线轮均采用三角形板单元。摆线轮与各针轮齿啮合情况，采用“点对地”的接触单元模拟它们的弹性接触。单元方向为摆线轮与各针轮齿啮合作用力的方向，即通过摆线轮与针轮啮合节点P。图11-67为摆线轮与针轮的有限元计算模型。

曲柄轴的偏心简化为刚性元以模拟轴的曲柄，这些空间刚性元的尺寸取决于曲柄轴的偏心距的数值。所以，将曲柄轴简化为空间梁元后，在曲柄轴与摆线轮的偏心轴处分

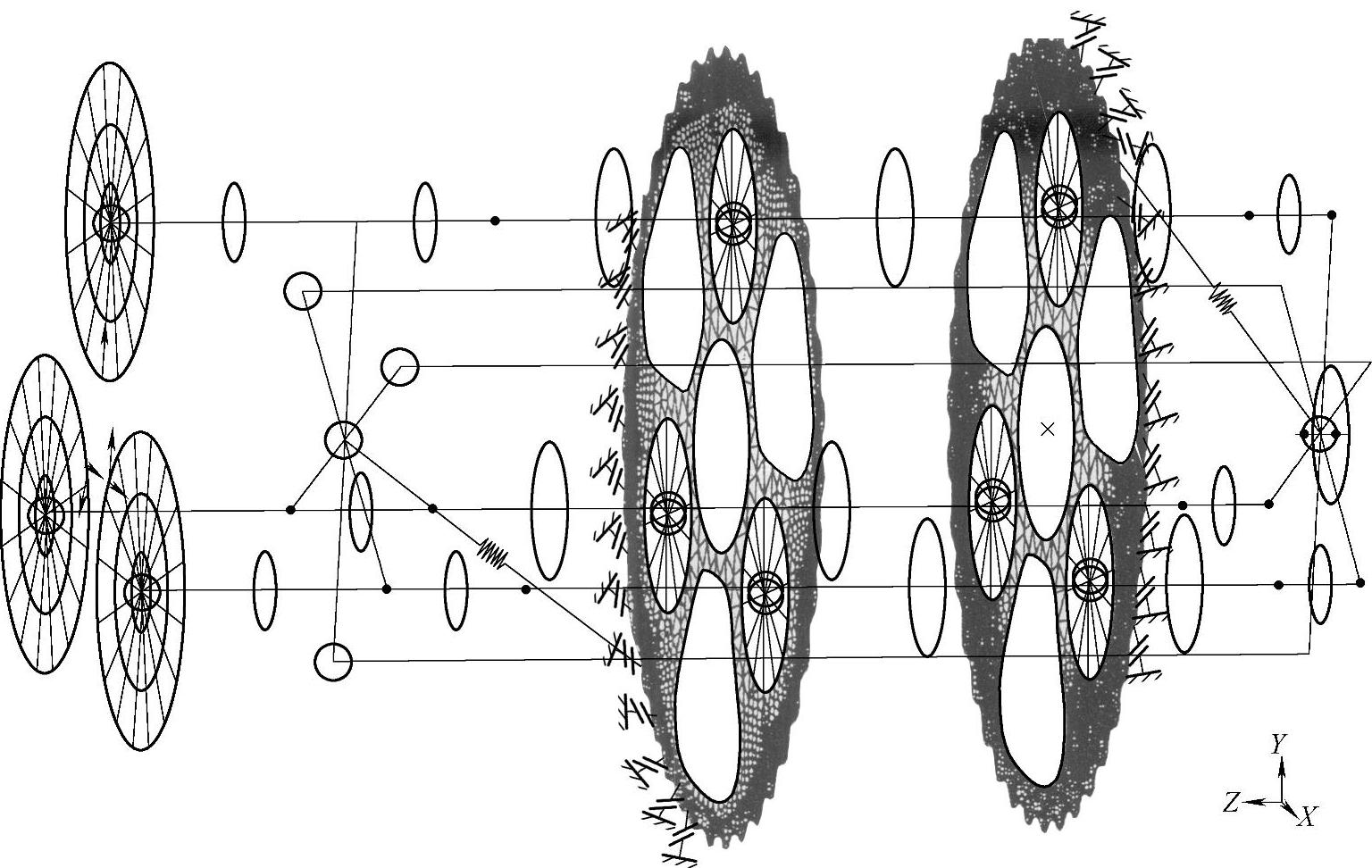
图11-66 RV传动系统的有限元计算模型

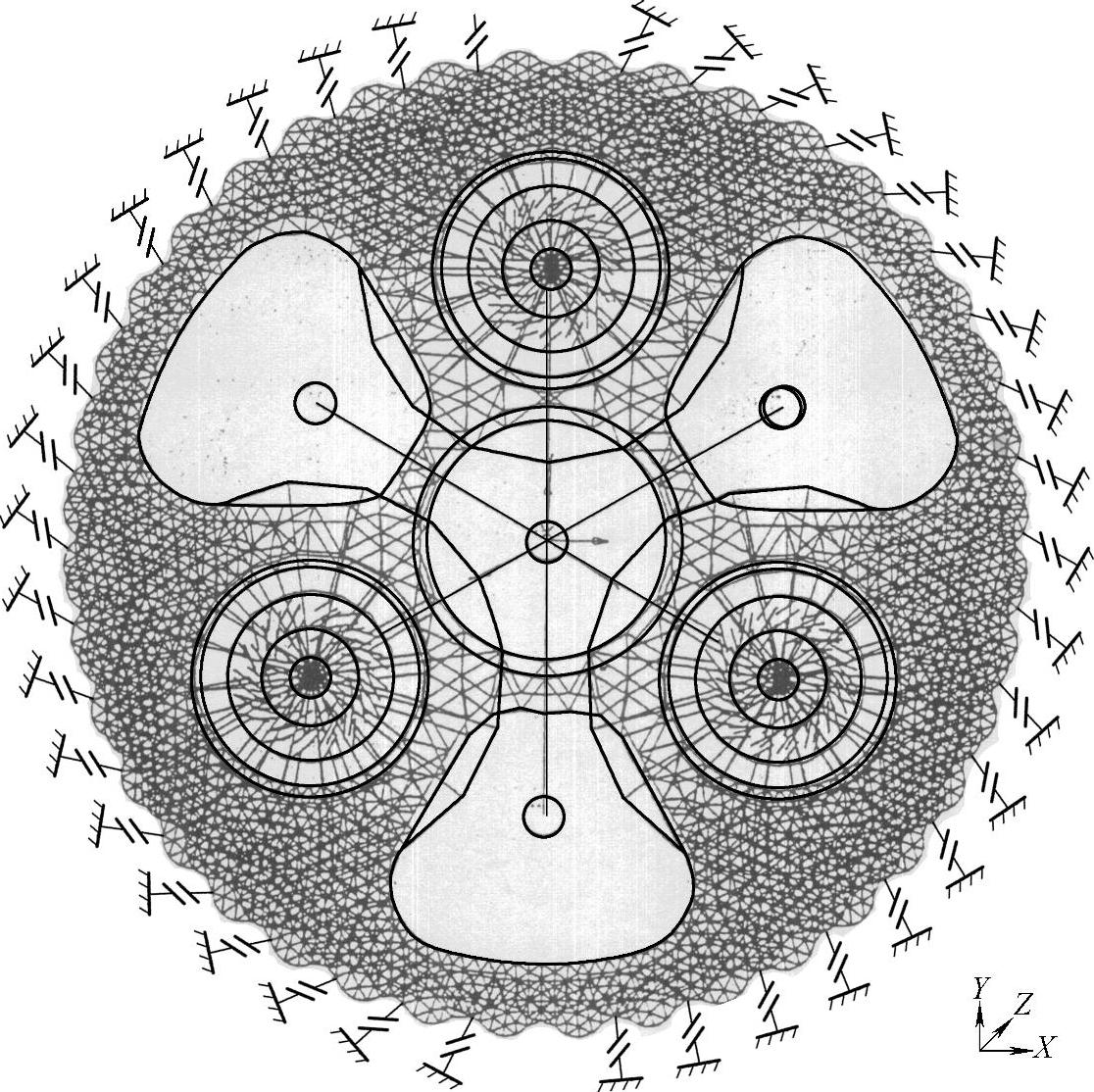
图11-67 摆线轮与针轮的有限元计算模型

别安放了若干个上述偏心值为其长度的刚性元。图11-68是行星架与曲柄轴的有限元计算模型。

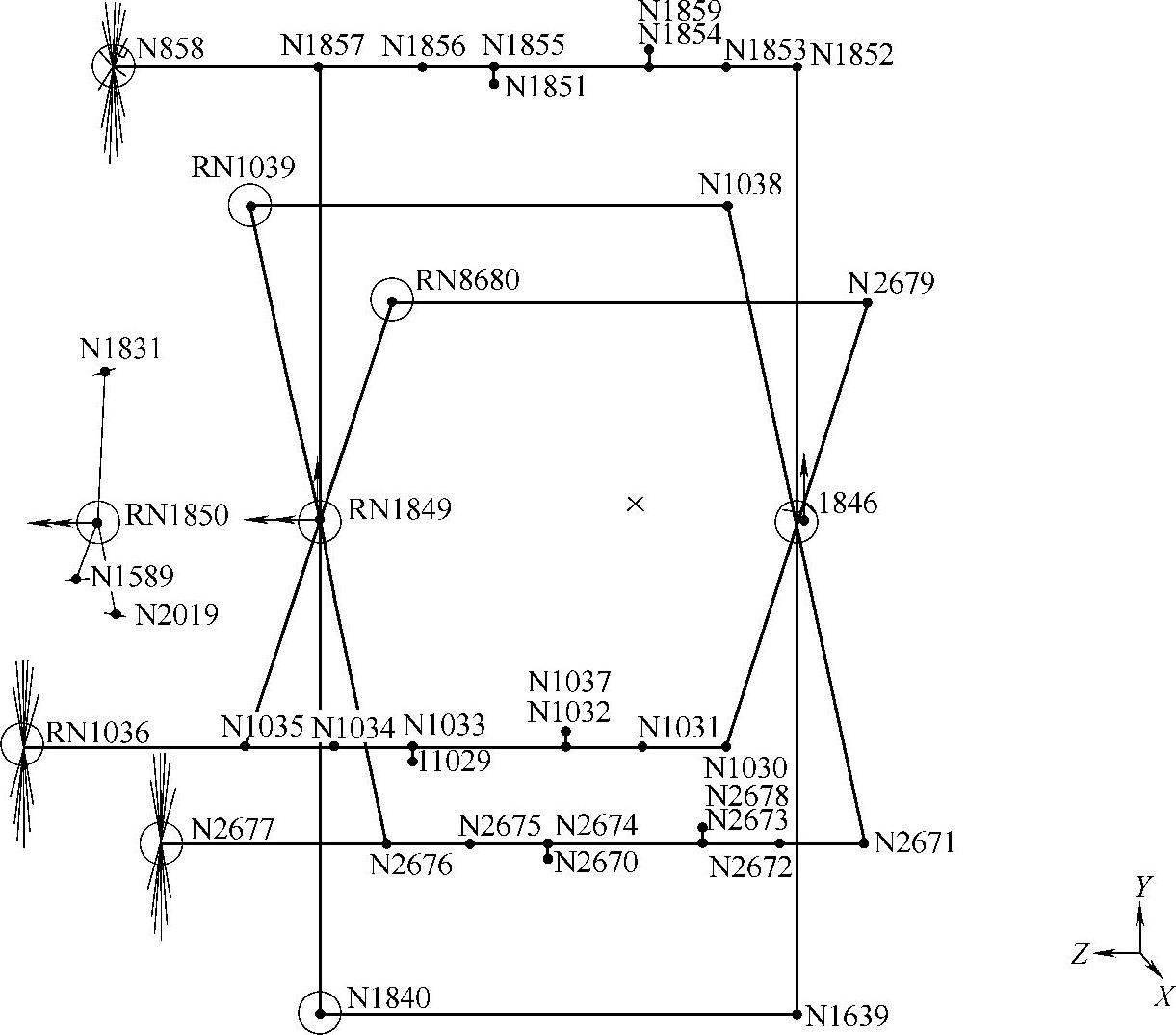
图11-68 行星架及曲轴的有限元计算模型

选用美国SDRC公司的I-DEAS软件系统，按此模型计算的渐开线齿轮传动、曲柄轴及行星架总体结构扭转刚度与前几节提出的计算模型所得结果进行对比列于表11-32中（以机器人用RV-60AⅡ减速器为例）。

表11-32 扭转变形计算结果

[1]因回转具有方向性，因此称回转矢量，常在机器人上使用。