作为机器人用的RV减速器,它必须具有高的运动和位置精度,这样才能使机器人的手爪精确地达到预定的位置。而在实际应用中,由于制造、安装误差,会使机器人的手爪不能很精确地达到预定的位置,所以设计上要解决的另一个关键问题是如何保证RV减速器具有高的运动精度。运动精度是衡量齿轮传动质量的一项重要的动态性能指标,通过传动误差来表示。
RV减速器的传动误差是指输入轴转动到任意角时,输出轴的理论转角与实际转角的角度误差。由RV减速器的组成可知,从输入到输出,主要通过渐开线齿轮传动、摆线针轮传动和摆线轮与输出盘之间的行星架输出机构而实现的。理论上输入轴和输出轴之间的传动比应该是不变值,但实际上由于组成RV减速器传动链的传动零件,在制造精度和装配精度上的误差,使瞬时速比发生变化,从而引起转角误差。因此,影响RV减速器的运动精度有以下3个环节。
1)渐开线行星齿轮传动部分。
2)摆线针轮传动部分。
3)摆线轮与输出盘之间的行星架输出机构。
由于摆线针轮传动部分和行星架输出机构部分对RV减速器传动误差的影响直接反映到输出轴上,因此影响程度大,而渐开线齿轮传动部分对RV减速器传动误差的影响还要考虑一个传动比,它对整机的影响要缩小相当于传动比那么多倍,因而影响相对要小得多。本节重点分析摆线针轮传动部分和行星架输出机构部分对RV减速器传动误差的影响。
1)行星架输出机构的传动误差分析
RV传动的摆线轮通过3个曲柄轴支承在输出盘上(图11-55),因此,输出机构是由3个双曲柄平行四边形机构(ABCD、ABEF、DCEF)组成的单自由度并联机构。理论上,输出盘的转角始终与摆线轮的相等,但实际上,各构件杆长的制造偏差和铰接副中的间隙,造成输出盘转角会有误差。由于这一机构是具有机构学中称之为虚约束的单自由度并联机构,这一误差还与各构件弹性条件有关。误差的精确分析必须考虑构件弹性条件在刚性误差分析的基础上进一步精确求解,这是一个高度非线性问题。本节主要着重讨论在刚体运动学范畴内机构的误差分析。
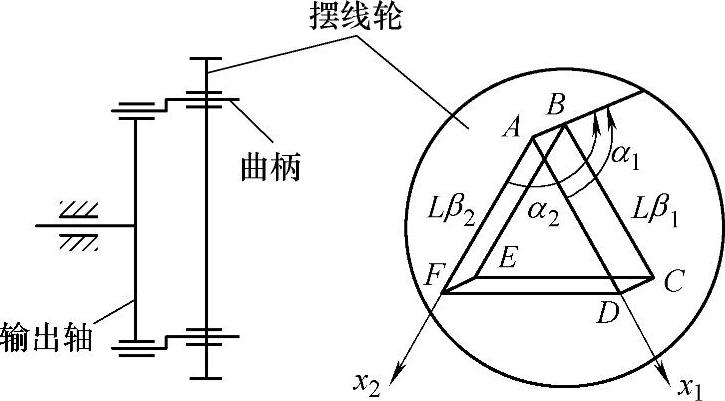
图11-55 输出机构(3个并联双曲柄平行四边形机构)
①双曲柄平行四边形机构的误差分析。当各杆长存在偏差时,其实际尺寸分别为l′i=li+Δli,当铰接副中存在间隙时,在关节力的作用下,各铰接副中两半铰中心Pi、Pj(即两相邻杆的端点)发生位移,见图11-56所示,其位移矢量可写为
Δp=(PiPj)=Δpfji (11-119)
式中 Δp——铰接副的半径间隙(mm);
fji——铰链p中杆j作用于杆i的关节力方向上的单位矢量。
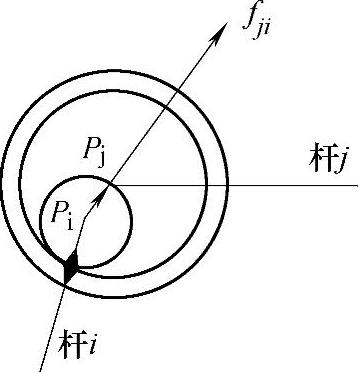
图11-56 铰接副中的间隙矢量
这样,当各杆长存在偏差,各铰接副中存在间隙时,不再构成平形四边形,机构误差分析的坐标系统就可以表示如图11-57所示,根据图11-57所示定义可以写出矢量方程
ΔA+l′1+ΔB+l′2+ΔC+ΔD-l′3=l′4 (11-120)
其投影方程可写为
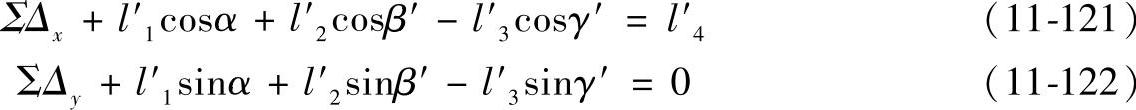
式中 β′——杆2的实际位置角(°),为名义值与误差之和,β′=β+Δβ,因杆2的名义位置角β=0,所以β′=Δβ;
γ′——杆3的实际位置角(°),为名义值与误差之和,γ′=γ+Δγ;
ΣΔx——4个间隙矢量之和ΣΔ沿x轴投影量(mm);
ΣΔy——4个间隙矢量之和ΣΔ沿y轴投影量(mm)。
由式(11-121)和式(11-122),消去γ′后可得
l′1l′4cosα+l′2l′4cosΔβ-l′1l′2cosα+
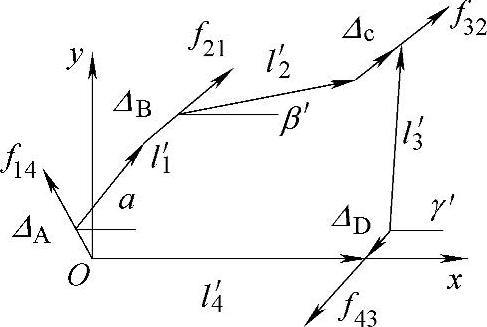
图11-57 四杆机构误差分析的坐标系统
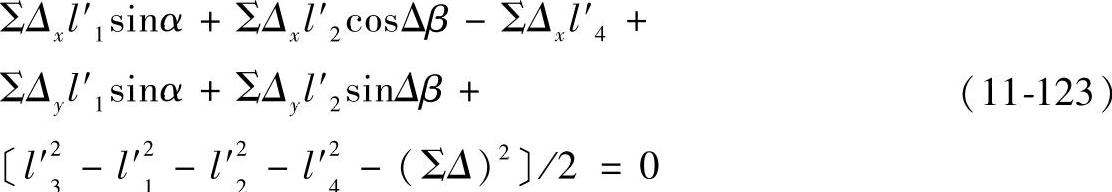
误差分析就是计算在给定α角情况下的位置角误差Δβ,即连杆(摆线轮)相对于输出杆的角度误差Δβ。由于Δβ很小,可应用近似式sin(Δβ)≈Δβ,cos(Δβ)=1-Δβ2/2,则由式(11-123)可得一关于Δβ的二次方程
a1Δβ2+b1Δβ+c1=0 (11-124)
式中
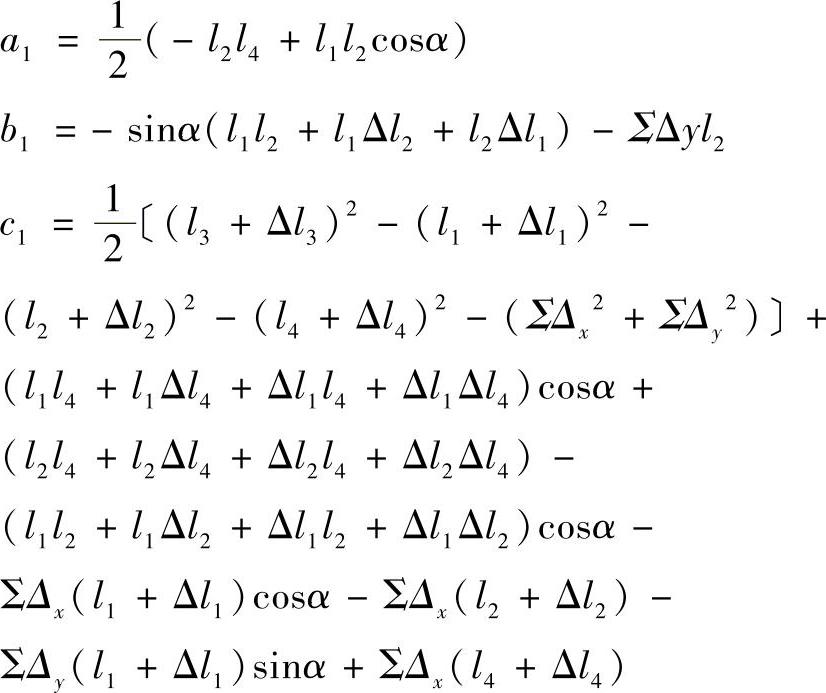
方程式(11-123)对Δβ有两个解值,分别对应于四杆机构的两个分支的位置。但对于某一给定的名义位置β下,角度误差Δβ只能有一个解值,或不存在解值(由于杆长误差太大,以至使四杆不能闭合)。但二次方程式(11-124)一般有两个解,其中它有一个是增根,增根产生的原因是采用近似公式cos(Δβ)=1-Δβ2/2而引起,可将方程所得的二个解代入原始式(11-123)进行验证后确定,但事实上,在两个增根中一个是微小量,即为所求的方程解的正确值。
②双曲柄平形四边形机构中铰接副间隙的补偿作用。双曲柄平行四边形机构中的四杆共线位置是一个对四杆长关系有严格要求的位置。当各杆长存在随机性偏差时,四杆有可能不能同时达到共线位置,从而破坏了双曲柄共存的几何条件。当机构在惯性作用下强行通过这一位置时,必须依靠杆件或轴承内部的弹性补偿,这使得机构受力增大。在刚性假定的条件下,则必须依靠铰接副中的间隙来补偿。
设各铰接副中半径间隙分别为ΔA、ΔB、ΔC、ΔD,对于曲柄1在左边的共线位置(图11-58a)来说:
a)当Δl1+Δl4<Δl2+Δl3,则杆1与杆4必然拉伸铰接副A,使它们的总长增加,而铰接副C受压,使杆2和3的总长缩短。当至少能达到图示的状态,四杆才能在共线位置上闭合,这时需满足条件
Δl1+Δl4+ΔA+ΔB≥Δl2+Δl3-ΔC-ΔD或写为ΣΔ=ΔA+ΔB+ΔC+ΔD≥(Δl2-Δl4)+(Δl3-Δl1)
b)当Δl1+Δl4>Δl2+Δl3(图11-58b),同理,应满足条件式
ΣΔ=ΔA+ΔB+ΔC+ΔD≥(Δl4-Δl2)+(Δl1-Δl3)
当曲柄1在右边的共线位置时,同样可以得出类似的条件式
ΣΔ=ΔA+ΔB+ΔC+ΔD≥(Δl2-Δl4)+(Δl1-Δl3)
ΣΔ=ΔA+ΔB+ΔC+ΔD≥(Δl4-Δl2)+(Δl3-Δl1)
综合上述4个条件式,应有
ΣΔ≥|Δl2-Δl4|+|Δl3-Δl1| (11-125)
上式说明,为了补偿杆长的制造偏差,使双曲柄平行四边形机构能够通过四杆共线位置,各铰接副中半径间隙之和应大于或至少等于连杆与机架(行星架)以及两曲柄之间杆长偏差之差的绝对值之和。
如前所述,RV传动的输出机构是由3个平行四边形组成的单自由度并联机构,其独立机构回路有两个,对于这样的机构,在刚性假设的前提下,也必须依靠铰接副中的间隙来补偿构件长度的偏差,才能保证可装配性条件。
可以证明,当平行四边形机构满足条件式(11-125)时,它不仅可以保证通过四杆共线位置,而且在曲柄任意位置下,总可以使得各对应杆保持在相互平行的位置。因此铰接副C必然可以闭合而把机构装配起来。由进一步推论不难知道,若并联机构中两个独立的平行四边形机构均能满足这一条件式(11-125),它们的相对边可维持相互平行的位置,这就保证了该并联机构的可装配性条件。
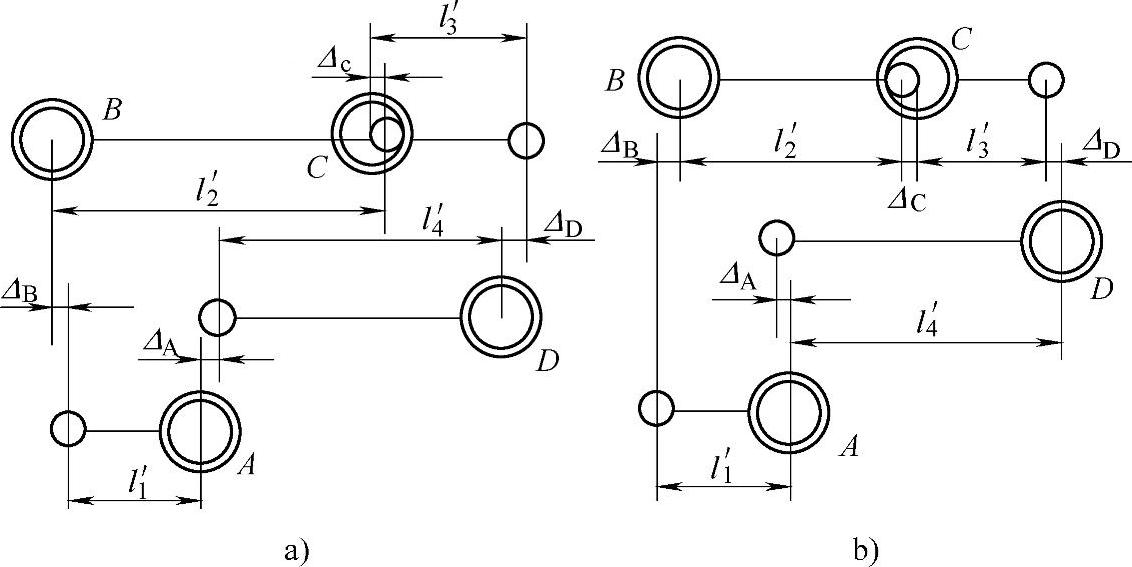
图11-58 四杆共线位置上杆长偏差与铰链间隙之间的关系(www.daowen.com)
③RV传动输出机构的刚性误差。RV传动输出机构具有3个回路,其中只有两个是独立回路。分别考虑两个独立回路各杆杆长的偏差和铰接副中间隙,其连杆与名义位置之间会有偏差,而且一般地说这两个连杆的位置角误差Δβ1和Δβ2不会相等。然而由于这两个连杆实际上是同一个刚性构件(摆线轮),因此必须有Δβ1=Δβ2。本节用两个独立回路中连杆在刚性假设下的误差来表示。设两个独立回路中的连杆在铰接副中的间隙范围内,左右的最大角度误差分别为Δβ′1、Δβ″1和Δβ2′、Δβ″2,若它们的数值关系又如图11-59所示,则并联机构的公共连杆摆线轮摆角误差范围为Δβ′1≤Δβ≤Δβ″2。
以机器人用RV-250AⅡ减速器的输出机构为例,进行传动误差分析。已知输出盘上曲柄轴孔间距离l4和摆线轮上转臂轴承孔间距离l2为109.119mm,曲柄偏心长度(即偏心距)l1=l3=2.2mm,曲柄位置以α1=60°,α2=120°(如图11-60所示)为例,①考虑杆长偏差同向分布与异向分布两种情况进行对比计算,结果见表11-29;②考虑铰链副(轴承)间隙的大小对角度传动误差的影响,结果见表11-30所示。
首先分别考虑两独立回路ABCD和ABEF中连杆各自可能的摆角范围。这里,可以假定各铰链中间隙矢量顺着曲柄的方向(图11-60),因为在这一状态下算得的摆角接近可能的最大值。①当连杆逆时针摆动,如图11-60所示的状态,可知ΣΔx=-(ΣΔ)cosα,ΣΔy=-(ΣΔ)sinα;②当连杆顺时针摆动时的状态,则间隙矢量反向,ΣΔx和ΣΔy均反号。先计算系数a1、b1、c1之值,再解方程式(11-124)的二根,并鉴别取其中正确值(微小量),即为连杆角度误差Δβ。
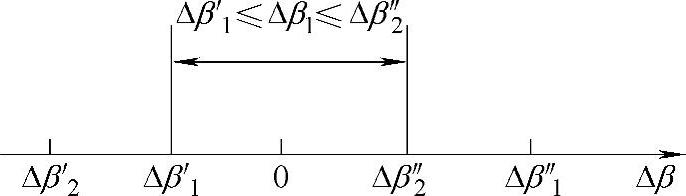
图11-59 公共连杆的误差范围
表11-29 杆长偏差对角度误差的影响

表11-30 轴承间隙对角度误差的影响
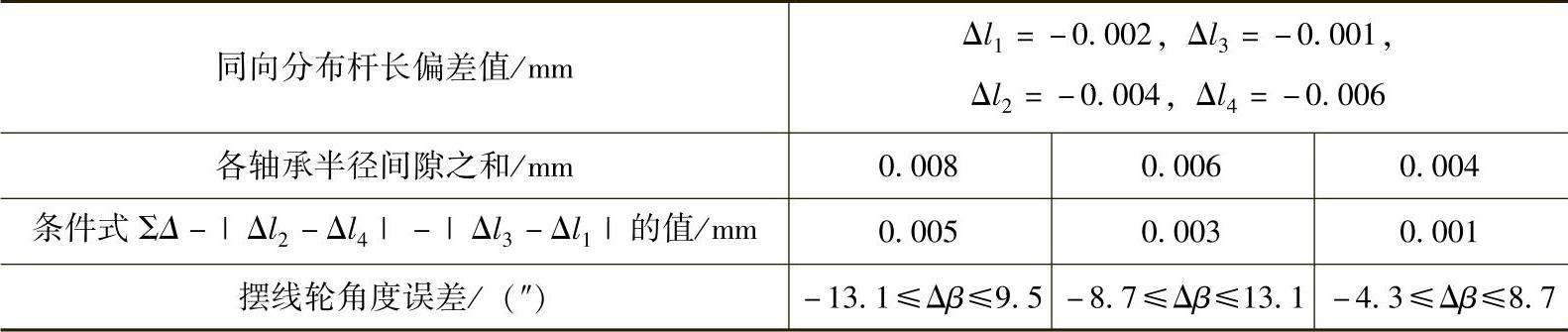
从表11-29计算结果可以看出,为了提高运动精度,机构中相对杆(1与3和2与4)的杆长偏差应该同向分布,故建议加工中应采取工艺措施,保证摆线轮三轴承孔与行星架三轴承孔一次装夹加工成形。从表11-30计算结果可以看出,为了提高运动精度,选择轴承间隙应该是在满足四杆共线条件下尽可能得小。
2)摆线针轮传动部分的传动误差
①小周期传动误差。小周期传动误差是当曲柄轴转一圈,即摆线轮转一个齿的过程中,引起输出轴的转角误差。摆线针轮传动部分影响小周期传动误差因素有
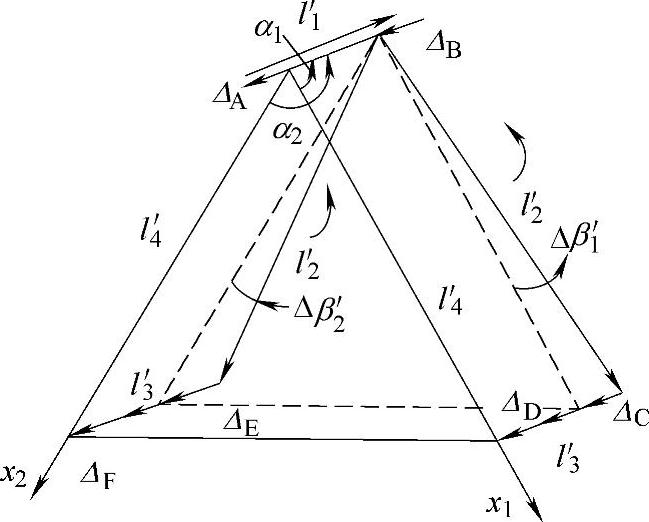
图11-60 半铰中心沿曲柄方向偏移状态下连杆的摆角Δβ′1和Δβ2′
a.针齿壳上针齿销孔圆周方向位置相邻误差δt1。参照式(11-107),针齿壳上针齿销孔圆周方向位置相邻误差δt1引起小周期传动误差

b.针齿壳上针齿销孔径向位置相邻误差δt2。参照式(11-106),针齿壳上针齿销孔径向位置相邻误差δt2引起小周期传动误差

c.摆线轮周节误差δfpt参照式(11-108),摆线轮周节误差δfpt引起小周期传动误差为

2)大周期传动误差。大周期传动误差是输出轴转一圈的过程中,输出轴的转角误差。影响RV传动大周期的误差因素有:
a.针齿壳上针齿销孔位置累积误差δFpl。参照式(11-107),针齿壳上针齿销孔位置累积误差δFpl引起大周期传动误差为

b.摆线轮周节累积误差δFp。参照式(11-108),摆线轮周节累积误差δFp引起大周期传动误差为

c.摆线轮齿圈径向圆跳动误差δFrl。参照式(11-106),摆线轮齿圈径向圆跳动误差δFrl引起大周期传动误差为

d.行星架组合件三孔相对于行星架支承大轴承安装基准位置误差Δ1。参照式(11-106),行星架组合件三孔相对于行星架支承大轴承安装基准位置误差Δ1引起大周期传动误差为

e.行星架支承大轴承径向圆跳动误差Δ2。参照式(11-106),行星架支承大轴承径向圆跳动误差Δ2引起大周期传动误差为

3)RV减速器的传动误差综合
①小周期传动误差综合。影响RV减速器小周期传动误差的因素有:摆线轮针轮传动部分和行星架输出机构部分。根据以上各因素对小周期传动误差影响的数学模型,按均值和公差来计算摆线轮针轮传动部分和行星架输出机构部分制造、安装误差及间隙所引起的小周期传动误差均值Δφs和公差TΔφs
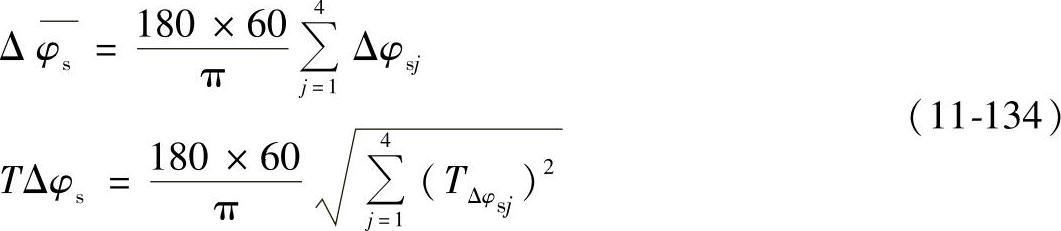
式中 TΔφsj——各误差因素引起小周期传动误差的公差(rad)(j=1~4)。其中,TΔφs4是1)节中Δβ1′≤Δβ≤Δβ2″引起的小周期传动误差的公差。
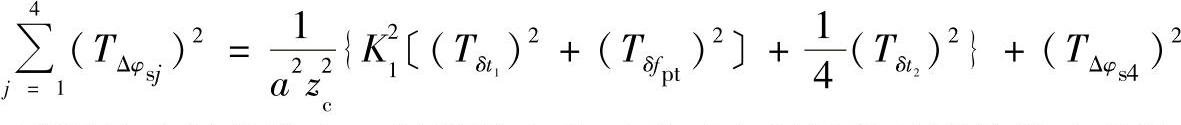
②大周期传动误差综合。根据以上各因素对大周期传动误差影响的数学模型,按均值和公差来计算引起的大周期传动误差均值ΔφB和公差TΔφB
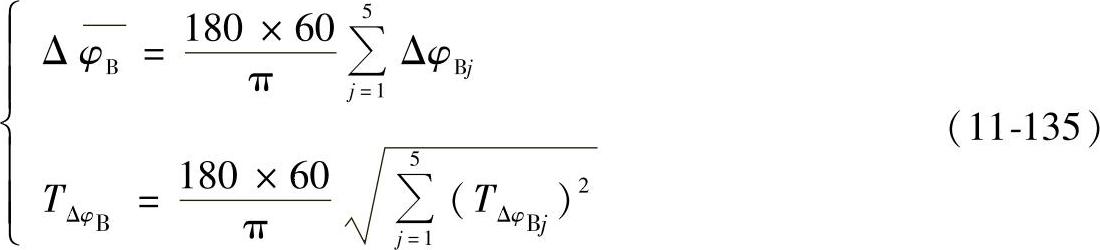
式中 TΔφBj——各误差因素引起大周期传动误差的公差(rad)(j=1~5)。
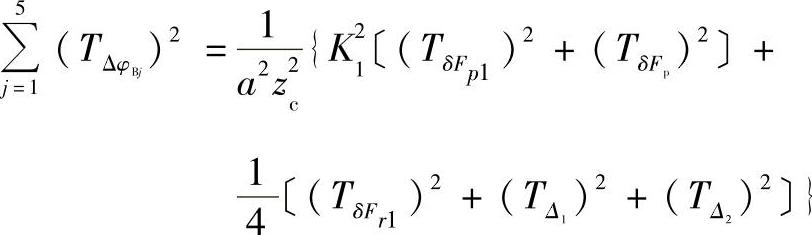
③传动误差综合。大小周期传动误差进行叠加,即可得RV减速器传动误差均值Δφ和公差TΔφ

因此,各因素引起RV减速器传动误差为

根据所优化设计的RV-250AⅡ减速器样机的各有关数据,将引起传动误差因素的数值代入传动误差计算式(11-136),得传动误差的均值和公差
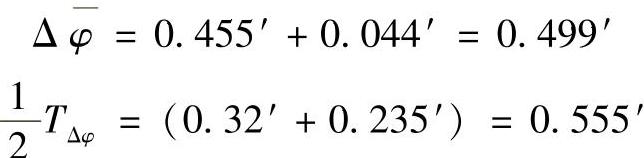
将传动误差的均值和公差代入式(11-137),得RV减速器的传动误差
Δφ=0.499′±0.555′=-0.056′~1.054′
=-3.36″~63.24″
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






