回差是指输入轴反向转动时，输出轴在运动上滞后于输入轴的现象。回差可以根据其产生的原因而分为三大类：一是单纯由于传动件几何尺寸、形状方面的原因所产生的回差；二是由于温度变形所产生的回差；三是传动件在工作时由于在负载的作用下存在弹性变形而产生的回差。这三类回差可以简单地称为：几何回差、温度回差和弹性回差。本章仅分析几何回差。

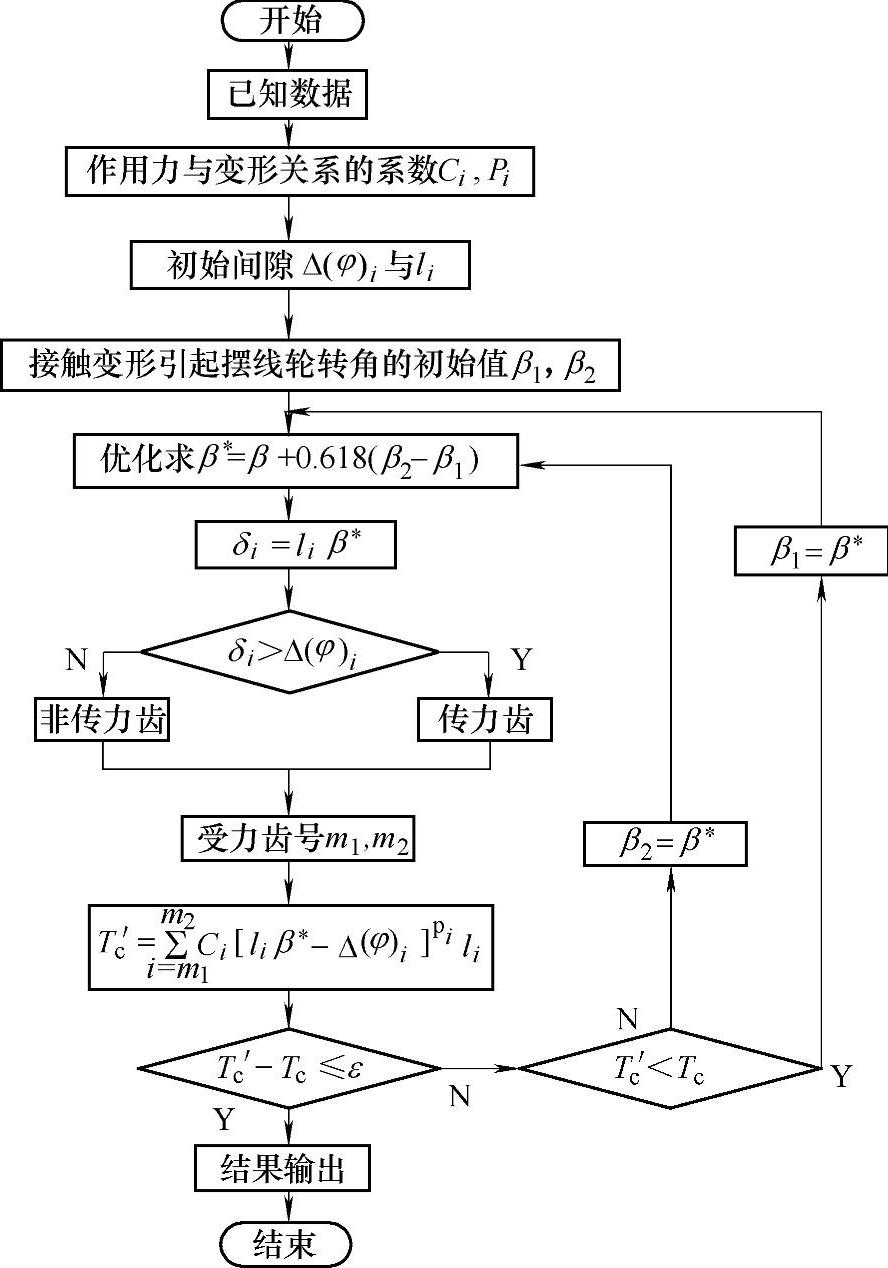
图11-54 摆线针轮受力分析程序框图

RV传动是由渐开线齿轮行星传动和摆线针轮行星传动组成的封闭差动轮系，因此，RV传动总的回差是由渐开线行星传动引起的回差和摆线针轮行星传动部分引起的回差两部分合成。摆线针轮传动部分的回差是直接反映到输出轴上的回差，影响程度最大，而渐开线齿轮传动对整机回差的影响还要考虑一个传动比，它对整机的影响要缩小相当于其传动比那么多倍，因而影响相对要小得多。

1）渐开线传动部分的回差分析 在渐开线圆柱齿轮传动部分中，影响该部分回差的主要因素有：

a）保证补偿制造误差和润滑的啮合间隙。

b）公法线平均长度偏差引起的齿轮侧隙。

c）中心距误差引起的齿轮侧隙。

d）齿轮径向综合误差引起的齿轮侧隙。

此外，还有轴线平行度误差，滚动轴承偏心，齿轮与轴的配合间隙等也不同程度影响回差，但它们的影响通常比较小。

①公法线长度平均偏差引起的齿轮侧隙。E_Ws、E_Wi分别为公法线平均长度的上偏差和下偏差，则公法线长度平均偏差ΔE_w的均值为

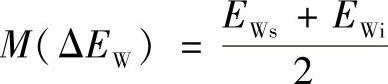
公法线长度平均偏差引起的圆周侧隙的均值j_E1和方差D（j_E1）为

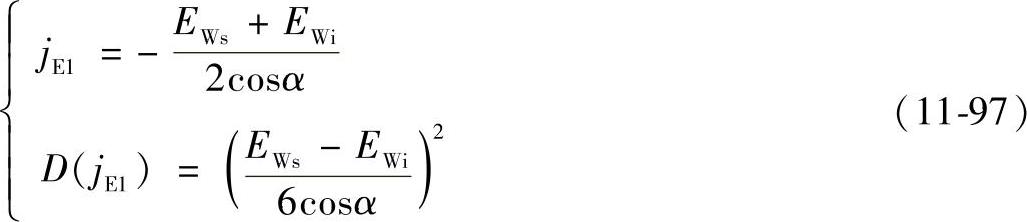
式中 α——渐开线齿轮传动的压力角（°）。

②中心距误差ΔF_α引起的侧隙。中心距误差引起的齿轮侧隙为常值的随机齿隙，假定中心距误差符合正态分布，则中心距误差引起的圆周齿隙的均值j_E2和方差D（j_E2）为

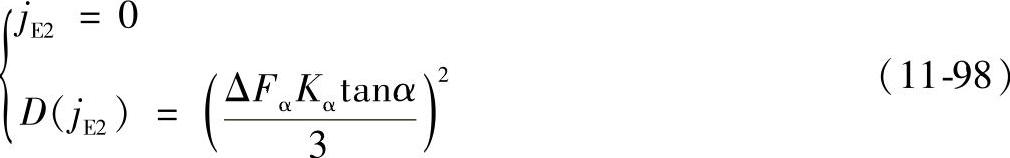
式中 K_α——换算系数，K_α=sinα′，α′为渐开线齿轮传动的啮合角（°）。③齿轮齿圈径向误差ΔF_r引起的齿轮侧隙。齿轮齿圈径向圆跳动的存在使得齿轮几何中心偏离回转中心，当量偏心距为，偏心距的径向分量对回差的影响与中心距误差的影响相类似，假定ΔF_r符合正态分布，则齿轮齿圈径向圆跳动引起齿轮的圆周侧隙的均值j_E3和方差D（j_E3）为

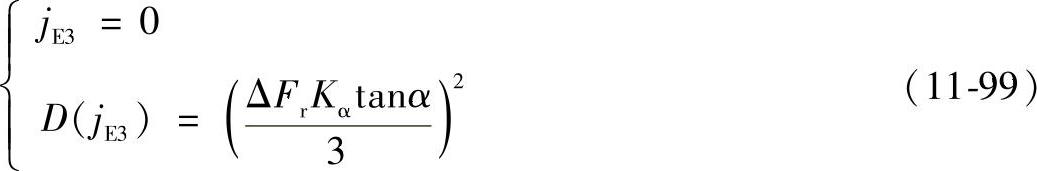
④渐开线齿轮传动部分回差的综合渐开线齿轮传动几何回差的均值Δφ₁₂和公差TΔφ₁₂为

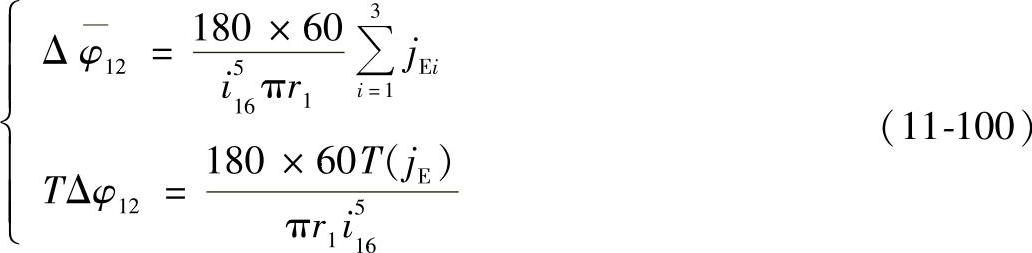
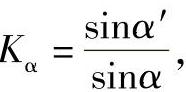
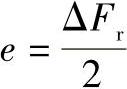
式中 T（j_E）——渐开线齿轮传动侧隙公差

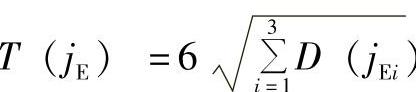
i⁵₁₆——RV传动的传动比，i⁵₁₆=i₁₆。

由此可得出渐开线齿轮传动部分引起RV减速器输出轴的回差Δφ12

2）摆线针轮传动部分的回差分析 理论上标准摆线轮与标准的针轮相啮合时，同时达到啮合的齿数约为针轮齿数的一半，且无啮合间隙。实际应用摆线针轮行星传动时，为补偿制造误差，便于装拆和保证润滑，摆线轮齿和针齿之间必须有一定的啮合间隙。啮合间隙的存在正是几何回差存在的内因。啮合间隙主要由摆线轮的修形、传动零件的制造误差和装配间隙引起。因此，在RV减速器中，影响该部分回差的主要因素有：

a）为补偿制造误差和便于润滑所需的正常啮合间隙，实际加工中，通常采用对摆线轮齿形进行移距和等距修形来保证。

b）针齿中心圆半径误差引起的侧隙。

c）偏心距误差引起的侧隙。

d）摆线轮齿圈径向圆跳动误差引起的侧隙。

e）针齿半径误差以及针齿销、孔的配合间隙引起的侧隙。

f）针齿销孔圆周位置度误差和摆线轮的周节累积误差引起的间隙。

g）摆线轮的修形误差造成的间隙。

h）转臂轴承间隙。

此外，偏心轴轴线与旋转轴轴线的平行度误差等也引起啮合侧隙的变化，因其影响程度较小，故不作讨论。

①摆线轮修形对回差的影响。在实际的摆线针轮传动中，为了补偿制造误差，便于装拆和保证良好的润滑，摆线轮齿与针轮齿之间是不允许没有间隙的，因此，实际的摆线轮不能采用标准齿形，而是都必须修形。

由于摆线轮修形在产生合理啮合间隙的同时，必会造成RV传动的回差，因此确定合理的啮合间隙和选择合理的修形方法，对保证整机只产生尽可能小的回差具有重要的意义。

若同时进行等距修形与移距修形，则摆线轮修形所引起的侧隙需摆线轮转过一转角，考虑摆线轮正反方向各存在一转角，所以，由等距修形与移距修形引起的回差Δφ₁为

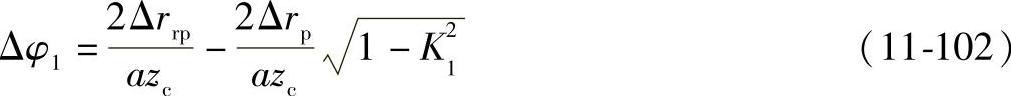
②针齿中心圆半径误差引起的回差。针齿中心圆半径误差的存在必然产生摆线轮与针轮之间的啮合间隙，从而引起回差，它对回差的影响和移距修形对回差的影响相同，因而针齿中心圆半径误差引起的回差Δφ₂为

式中 δr_p——针齿中心圆半径误差（mm）。

③针齿销半径误差引起的回差。针齿销半径误差对回差的影响与等距修形类似，因而针齿销半径误差引起的回差Δφ₃为

式中 δr_rp——针齿销半径误差（mm）。

④针齿销与针齿销孔的配合间隙对回差的影响。针齿销与针齿销孔的配合间隙对回差的影响与等距修形类似，因而引起的回差Δφ₄为

式中 δj——针齿销与针齿销孔的配合间隙（mm）。

⑤摆线轮齿圈径向圆跳动误差引起的回差。摆线轮的齿圈径向圆跳动误差引起的最大回差

式中 ΔF_r1——摆线轮的齿圈径向圆跳动误差（mm）。

⑥针齿销孔圆周位置度误差引起的回差。由于加工误差的存在，使针齿圈上安装针齿销的孔产生圆周位置度误差，针齿销孔圆周位置度误差引起的回差为

式中 δt_Σ——针齿销孔圆周位置度误差（mm）。

⑦摆线轮周节累积误差引起的回差。摆线轮周节累积误差为ΔF_p时，消除该误差产生的啮合侧隙所引起的摆线轮的转角，即引起的回差(www.daowen.com)

式中 ΔF_p——摆线轮周节累积误差（mm）。

⑧修形误差和偏心距误差引起的回差。摆线轮的齿形修形量是在设计时给出的，在实际加工中，由于机床调整和装夹误差，使实际的修形量偏离设计修形量，从而产生修形误差影响侧隙。对式（11-102）按泰勒级数在（Δr_rp，Δr_p，a）处展开，并略去误差的平方以上项得

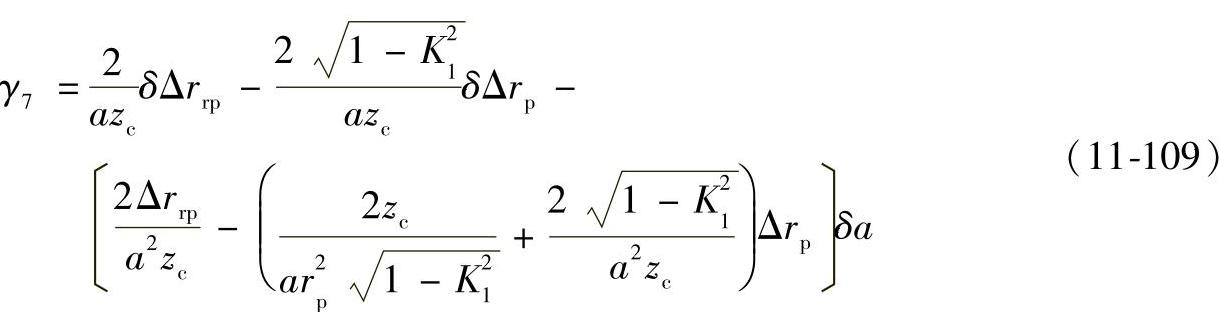
式中 δa——偏心距误差（mm）；

δΔr_rp——等距修形误差（mm）；

δΔr_p——移距修形误差（mm）。

令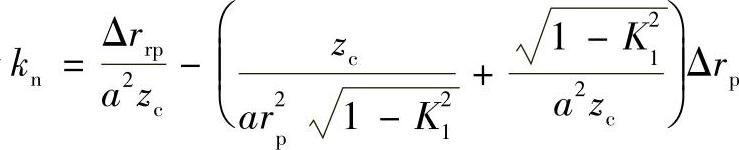，则等距修形误差、移距修形误差和偏心距误差引起的回差

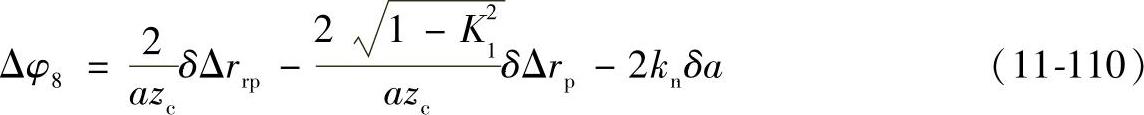
⑨摆线针轮传动部分回差综合。根据以上各因素对回差影响的数学模型，按均值和公差来计算摆线针轮传动部分引起的回差均值Δφ₄₅和公差T_Δφ₄₅。

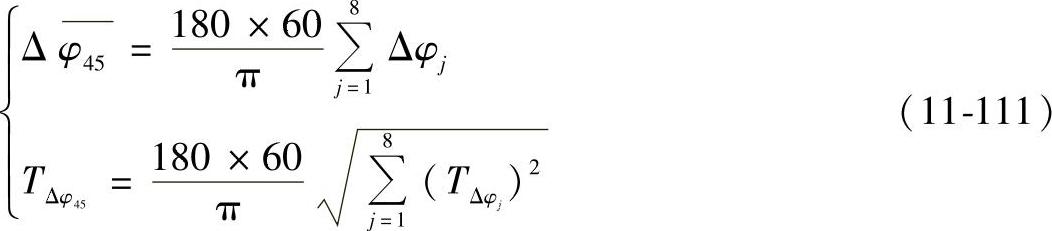
式中 T_Δφ_j——各误差因素引起回差的公差（rad）（j=1～8）。

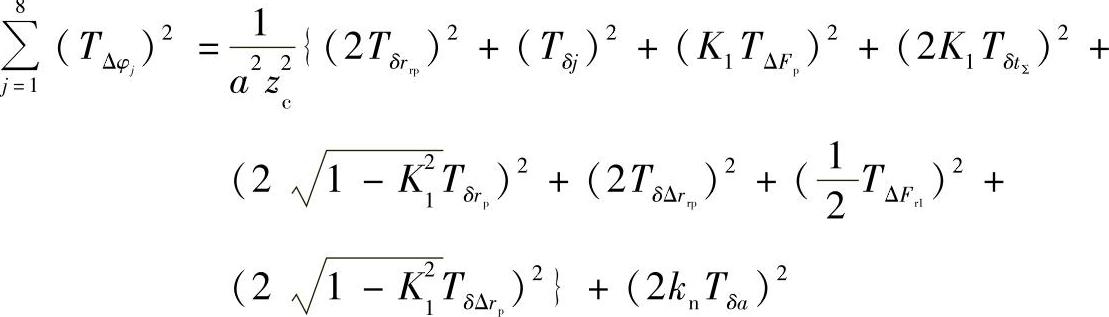
则摆线针轮传动部分引起RV传动输出轴的回差为

3）轴承间隙对回差的影响RV减速器的转臂轴承存在一定的游隙，必然会对回差产生影响。当存在轴承游隙时，摆线轮啮合转动后，必须先消除轴承游隙的影响才能够引起输出，则消除游隙所需的摆线轮空转角，即所引起的回差均值Δφ_u及公差T_Δφu

式中 Δu——转臂轴承的游隙均值（mm）；

T_Δu——转臂轴承的游隙公差（mm）。

则轴承游隙引起RV传动输出轴的回差为

4）传动系统总的几何回差的数学模型 对于二级传动的RV减速器，依次将各级传动的回差，通过传动比的缩放关系，综合出输出轴上传动系统的几何回差的均值ΔφΣ和公差TΔφΣ

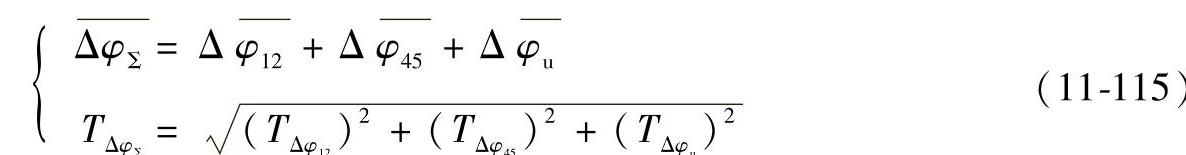
式中 Δ_φΣ——RV减速器总几何回差均值（′）；

T_ΔφΣ——^RV减速器总几何回差公差（′）。

因此，各因素对RV传动的总回差为

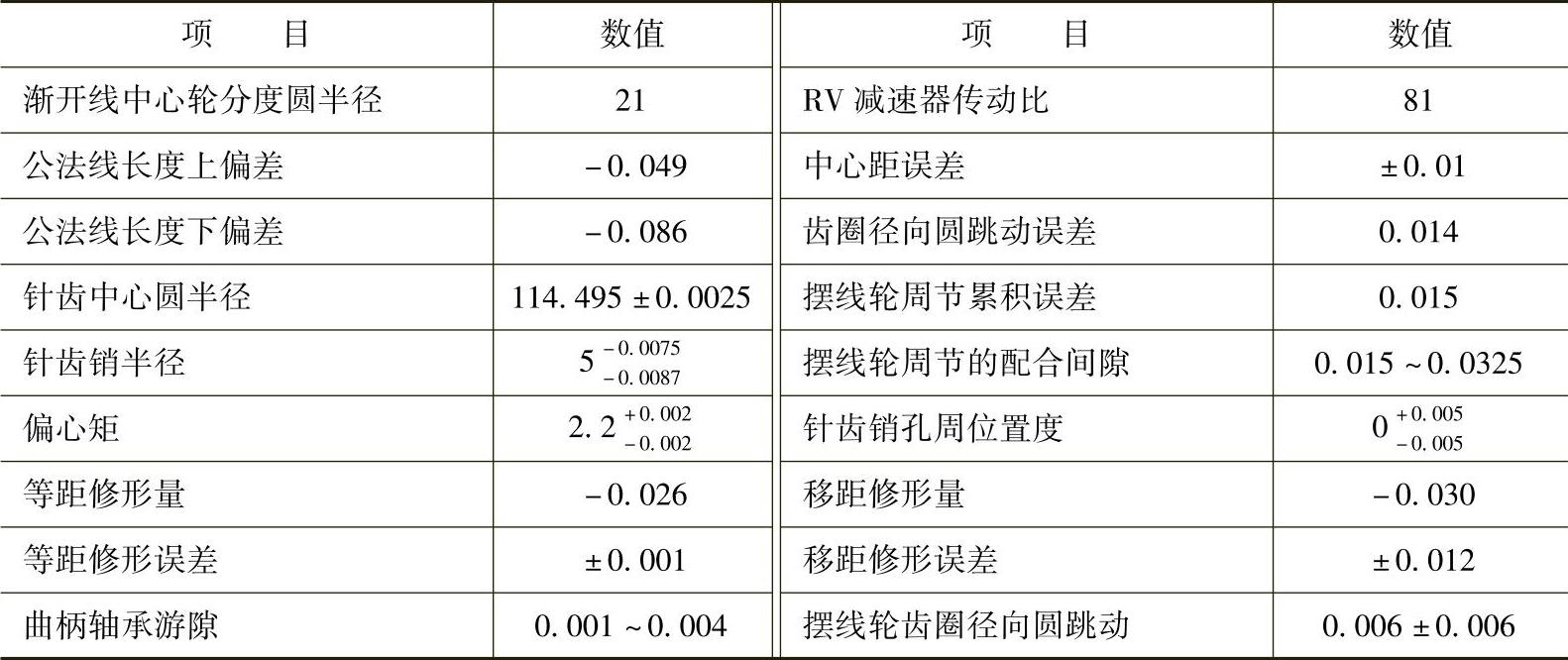
以机器人用RV-250AⅡ减速器为例，根据所优化设计的RV减速器图样，得到影响回差的各参数误差见表11-26。

将表11-26中各误差值代入回差数学模型式（11-115），计算出RV传动的回差均值ΔφΣ和公差TΔφΣ为

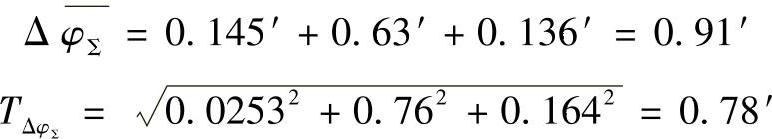
则所优化设计的机器人用RV-250AⅡ减速器样机的回差ΔφΣ计算值为

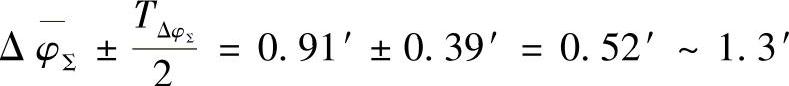
5）回差的敏感性分析 由于影响回差的因素很多，为了找出影响回差的主要因素，在设计中选择制造精度时能分清主次，故必须进行回差的敏感性分析。

表11-26 参数误差表 （单位：mm）

①敏感性分析原理。对于函数

Y=Y（x₁，x₂，…，x_n）

当x_i存在误差Δx_i，并在较小的情况下按泰勒级数展开，略去高于线性的各项，这样就可得到熟悉的误差计算方程

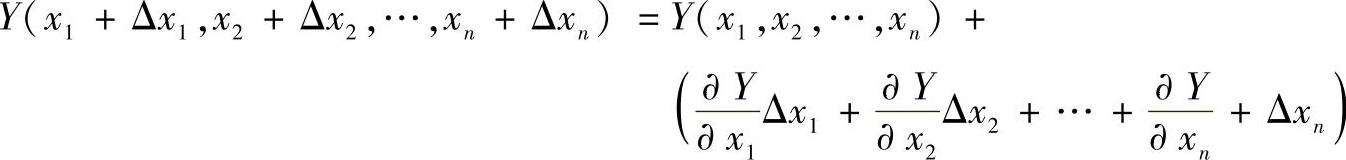
其中函数Y=Y（x₁，x₂，…，x_n）的误差为

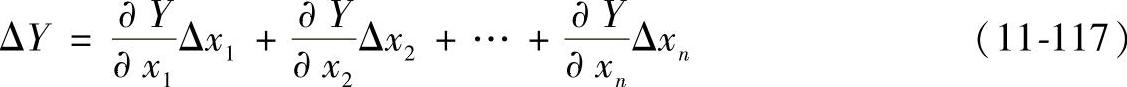
一般，敏感性指数定义为

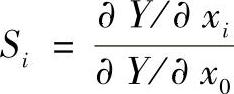
上式中的∂Y/∂x₀是作为参照的一个输入误差参数。通过敏感性指数，可以比较相应的参数误差Δx_i对函数误差ΔY的影响程度，确定引起最大函数误差的参数。当x_i的值确定时，偏导数∂Y/∂x_i为常数，因而式（11-117）可写成

ΔY=g₁Δx₁+g₂Δx₂+…+g_nΔx_n

同样，敏感性指数也可表示为

②摆线针轮传动部分各影响因素的敏感性分析。由于摆线针轮传动部分对回差的影响是直接反映到输出轴上的回差，因此其影响程度最大。但摆线针轮传动部分中的各因素对回差的影响程度如何，就必须对摆线针轮传动部分进行回差的敏感性分析，从中找出对回差影响大的因素，使我们能在设计制造过程中加以控制。根据摆线针轮传动中各误差因素对回差影响的模型，按照回差敏感性分析原理，对摆线针轮传动中的各项影响因素进行敏感性分析，结果见表11-27所示。

表11-27 参数误差系数和敏感性指数

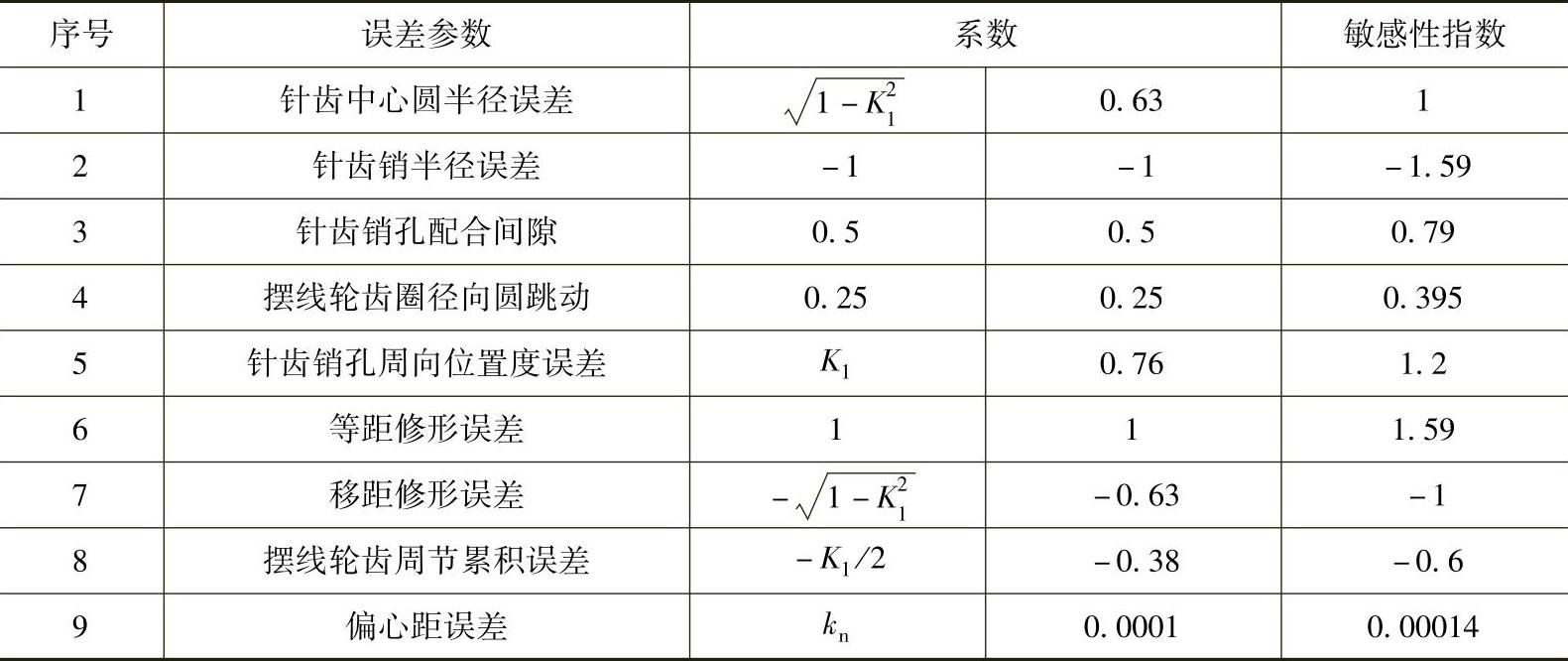
从表11-27可以看出，针齿销半径误差、针齿销孔周向位置误差及等距修形误差具有最大的敏感性指数，对回差的影响最大，而偏心距误差的敏感性指数最小，约为针齿中心圆半径误差敏感性指数的0.01%，它对回差的影响很小，在误差值较小的情况下，可以不考虑。敏感性指数为负值，说明当该项因素具有正向误差时，它使回差减小。

③摆线轮修形方式对回差的影响。如前所述，对回差要求极严的机器人用RV传动，应当采用负等距和负移距修形组合，因为它不仅与正等距和正移距修形组合一样，可以通过优化设计确定合理的修形量，使修形后的摆线轮齿与针轮齿互为共轭齿形。既可保证瞬时传动比恒定，从而传动平稳，又可获得理论上的多齿啮合，保证提高承载能力，而且，在同样径向间隙条件下，它引起的回差可比正等距和正移距修形组合小得多，两种不同修形方式引起回差的对比计算结果见表11-28。

表11-28 不同修形方式对回差的影响

从表11-28可以看出，在同样径向间隙的条件下，采用负等距和负移距修形组合方法可以使摆线轮齿形与针轮齿啮合时所引起的回差只为采用正等距和正移距修形时引起的回差的15.6%。后者的修形组合只适用于对回差要求不高的动力传动。