RV传动的传力机构是由平行四边形机构组成的单自由度并联机构。摆线轮1和2各通过3个平形四边形机构（GABH、HBCI、ICAG和GDEH、HEFI、IFDG）分别与输出盘相联，如图11-48所示。这3个平行四边形机构中有2个是运动学上的独立回路。这种单自由度并联机构，在运动学上说是具有虚约束的机构，在静力学上说是静不定系统。这种静不定系统的力分析除了要满足静力平衡条件外，还与机构中有关弹性环节的变形协调条件有关。

下面以3个曲柄轴（互成120°轴对称布置）的RV传动为例，把组成减速器各传力构件拆开，分别取各构件为分离体，进行力分析。

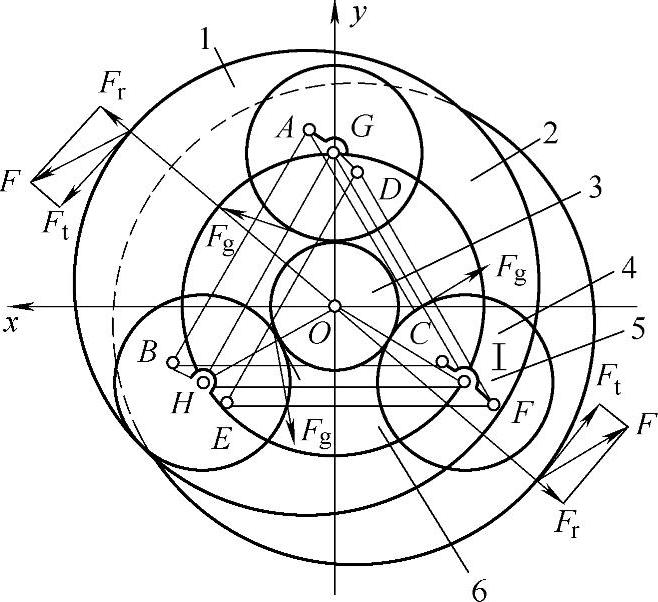
图11-48 RV传力机构图

1、2—摆线轮 3—中心轮 4—行星轮 5—曲柄 6—输出机构圆盘

渐开线行星齿轮传动的中心距用a₀表示，摆线针轮行星传动的偏心距用a表示。

1）取摆线轮1为分离体，受力简图如图11-49a所示。

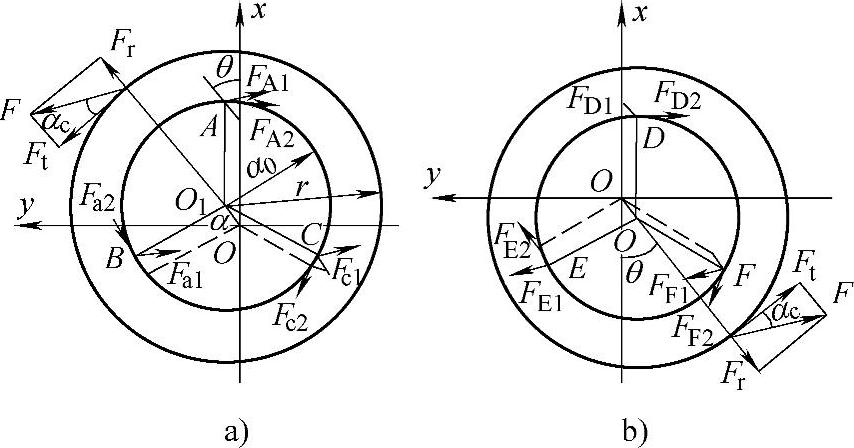
图11-49 摆线轮受力简图

a）摆线轮1 b）摆线轮2 F—针齿作用在摆线轮上的总合力，可分解为切向分力F_t和径向分力F_r

F_ij—表示i点的作用力，j=1表示由F引起沿F方向的作用力，j=2表示由力矩T_c=F_tr′_c引起的作用力

r′_c—摆线轮节圆半径；θ—曲柄转角

由于摆线轮刚度很大，可认为传力过程中，在摆线轮上安装曲柄轴承的3个孔间距离是基本不变的，而曲柄轴承相对摆线轮来说，可看成是弹性的。在3个曲柄的尺寸完全相等（没有尺寸偏差），滚动轴承没有初始径向间隙（或间隙完全相等）的理想状态下，可认为3个曲柄销上沿针齿对摆线轮的力F方向上的弹性位移量相等，由于曲柄结构与尺寸完全相同，其刚度条件相同，所以认为摆线轮与3个曲柄轴承处，在此方向的分力相等，均为F/3。同样，在转矩T_c作用下，3个曲柄销轴承处沿摆线轮半径垂直方向（切向）的弹性位移量相等，从而认为这3个方向上的分力（切向力）也相等，大小为T_c/（3a₀）。上述分析可以看出，3个曲柄轴承处的上述2个分力大小分别相等，但其合力与曲柄轴的位置及曲柄转角θ有关。

当曲柄转角为θ时，针齿作用摆线轮的力F可用矢量矩阵表示为

则3个曲柄作用在摆线轮上的力分别为

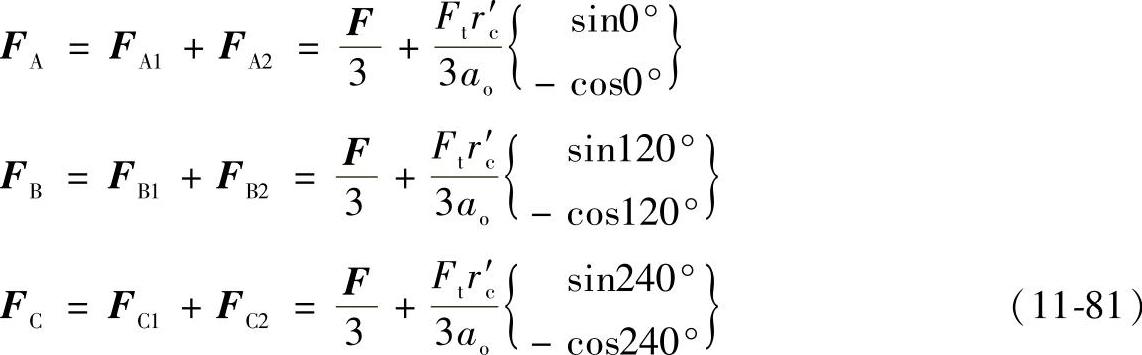
2）取摆线轮2为分离体，如图11-49b所示。因两片摆线轮互成180°，且结构与尺寸完全对称，在机构名义尺寸（无制造偏差）理想状态下，它们所传递的功率应相等，可得出针齿作用给两片摆线轮的力大小相等，方向相反。因而，3个曲柄销（D、E、F）上的作用力F_D1、F_E1、F_F1与摆线轮1上的3个曲柄销（A、B、C）上的作用力F_A1、F_B1、FC1分别大小相等方向相反。

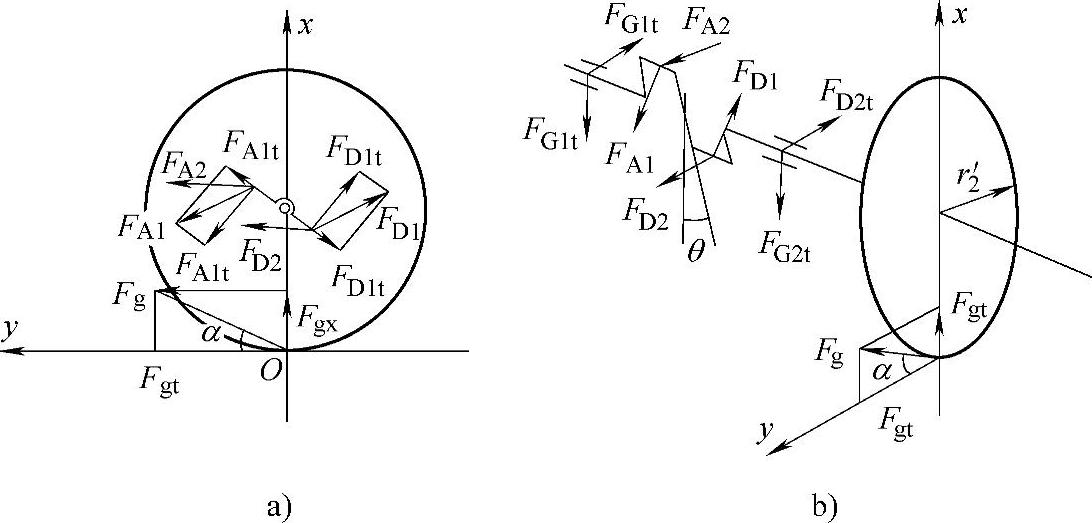
3）取任一曲柄轴及与其相固联的行星轮为分离体，如图11-50所示。

(www.daowen.com)

图11-50 曲柄轴及行星轮受力简图

由图11-50a，可以根据力矩平衡方程得出

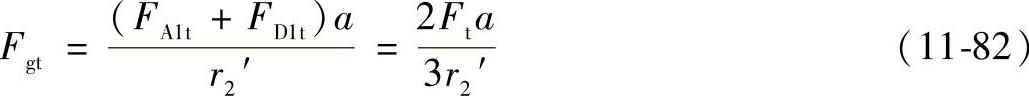
式中 F_gt——行星轮所受的切向力；

F_A1t——F_A1的切向分力，见图11_-50a；

F_D1t——F_D1的切向分力，见图11_-50a；

r₂′——行星轮节圆半径。

由式（11-82）可知，行星轮所受的啮合力是与曲柄转角θ和曲柄位置无关的，3个行星轮所受的啮合力大小相等。因此，渐开线中心轮的输入转矩T₁为

式中 r′₁——中心轮节圆半径。

由图11-50b可知，作用力F_A、F_D和F_gt已知，而未知力只有曲柄轴两端支反力，由水平和垂直平面内的力和力矩平衡方程，即可解出支反力F_G1和F_G2。

4）对于两端支承的整个输出机构，同样可由水平和垂直面内的力和力矩平衡方程，求出输出机构支承轴承处的支反力。

以上根据RV传动的具体结构，提出基本上符合实际的变形协调条件，使复杂的静不定系统的力分析得以简化，并成为在工程上实用的力分析方法。应该指出，这一变形协调条件是针对机构尺寸没有误差与轴承中没有初始径向间隙（或各轴承初始间隙完全相等）的理想（名义）状态提出的，因此，作出的力分析是名义力分析。精确计算还需考虑实际制造偏差，引入适当的载荷不均匀系数。

根据以上对RV传动的受力分析，可编制出相应的力分析程序，在计算机上计算出曲柄转角θ为任意位置的各传力构件上的所有作用力。

例11-4 对针齿中心圆直径d_p=229mm的RV-250减速器进行力分析，其基本参数见表11-25，力分析结果见图11-51。

表11-25 RV-250减速器基本参数

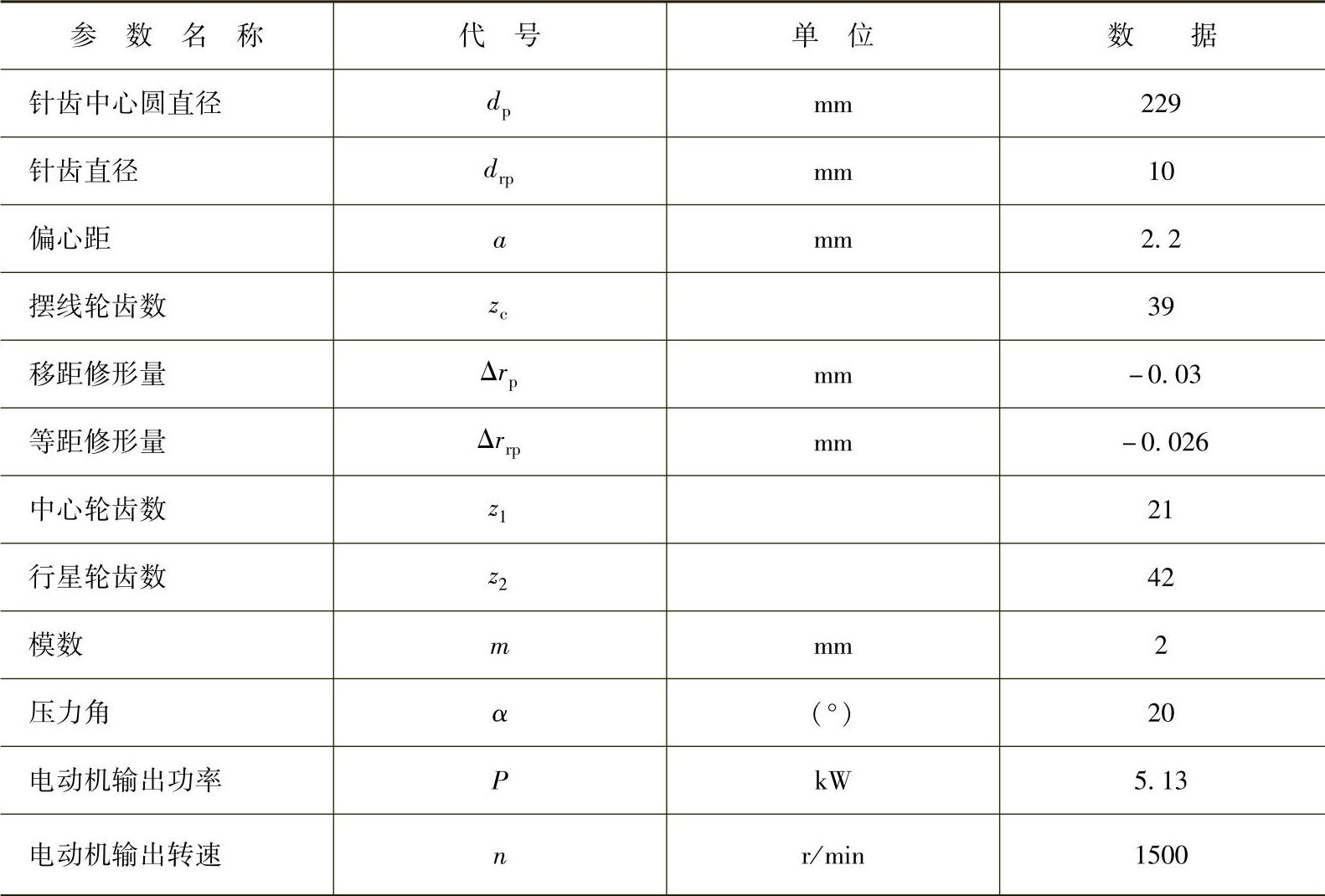
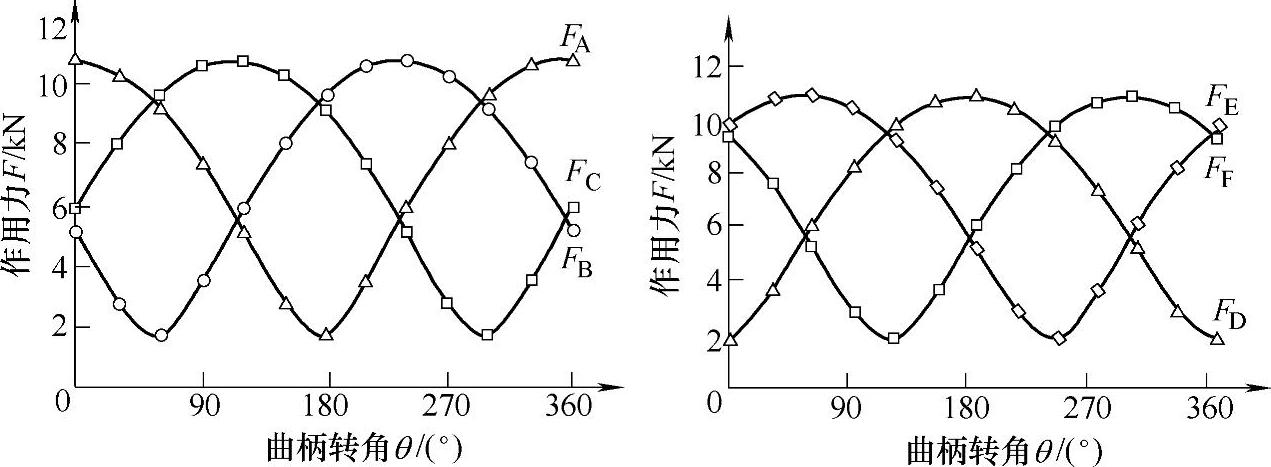
图11-51 力分析结果