摆线针轮行星传动的针齿中心圆直径d_p及外廓安装尺寸均已标准化，在这种情况下，能有效地影响传动承载能力的主要参数是偏心距a、针齿半径r_rp，参数优化就是根据给定的d_p，z_p，z_c，以减速器能承受的额定输出转矩T最大为目标函数，来优选a与r_rp，即：

设计变量：X=[x₁，x₂]^T=[a，r_rp]^T

目标函数：T（a^*，r^*_rp）=maxT（a，r_rp）

1）参数优化的约束条件的确定

①偏心距a约束条件：偏心距a应确保其短幅系数K₁在合理的取值范围内，即

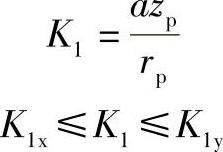
如第3节所述，K₁的取值不同，摆线轮的齿形就不同，会影响摆线针轮传动的性能，是一个很重要的参数，其值既不能过大也不能过小。K₁的比较合理的范围值可由表11-3来确定。

②针径系数的约束条件：针齿半径r_rp的取值应满足避免针齿相碰及保证针齿和针齿壳强度两项要求，即r_rp应确保其针径系数K₂在合理的取值范围内

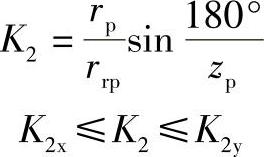
K₂值的范围由表11-4来确定。

③针齿半径r_rp的约束条件：针齿半径r_rp的取值应满足摆线轮不产生顶切、尖点的要求，也就是r_rp应小于摆线轮齿凸齿形部分的理论齿形最小曲率半径|ρ₀|_min。由2.4.1节内容可知：

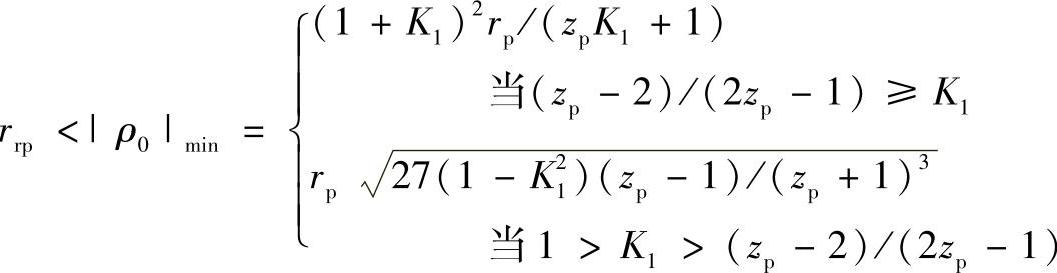
④偏心距a的取值范围应符合摆线磨齿机的规范，即可选用的a（mm）值为0.65，0.75，1，1.25，1.5，2，2.5，3，3.5，4，4.5，5，5.5，6，6.5，7，8，9，10，11，12，13，14。

⑤针齿直径应取为整数，以便于系列化。

⑥摆线轮与针齿接触强度的约束条件：

摆线轮齿与针轮齿的最大接触应力根据式（11-70）为

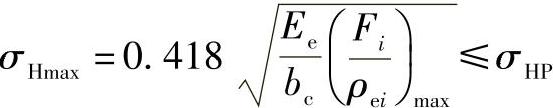
式中各项符号的意义见本章5.1节。

⑦转臂轴承的寿命L_h不小于许用值Lp

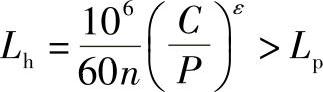(www.daowen.com)

式中各项符号的意义见本章第8节。

综上所述，得以下约束函数

其中（F_i/ρ_ei）max是x（a，r_rp）的函数

g₉（a，r_rp）=L_p-〔10⁶/（60n）〕（C/P）ε≤0

其中P是x（a，r_rp）的函数。

2）参数优化过程 对摆线减速器的一般计算过程是：由减速器传递的额定转矩T确定各部分参数后，再计算针齿受力齿数及受力分布情况及轴承受力情况，得出强度、轴承寿命等项指标，再与许用值进行比较，检验是否合格。

但是参数优化中作为目标函数的T与设计变量a，r_rp之间的函数关系较为复杂，无法用一个或多个简单明了的解析式来表达，因此可用下述方法处理：

①给目标函数T一个初始值T₀₀，对满足前5项约束条件（即前7个约束函数）的点x（a，r_rp），计算当输出转矩为T₀₀时的强度和转臂轴承寿命。设约束条件中的第6项计算值为J₁，许用值为A₁，二者的比值为JA₁，第7项的计算值为J₂，许用值为A₂，二者的比值为JA₂。若在转矩为T₀₀时，满足0.995≤（JA_i）max≤1（i=1，2），则T₀₀即为该点的目标函数值；若（JA_i）max<0.995，则进行第2步；若（JA_i）max>1则进行第3步。

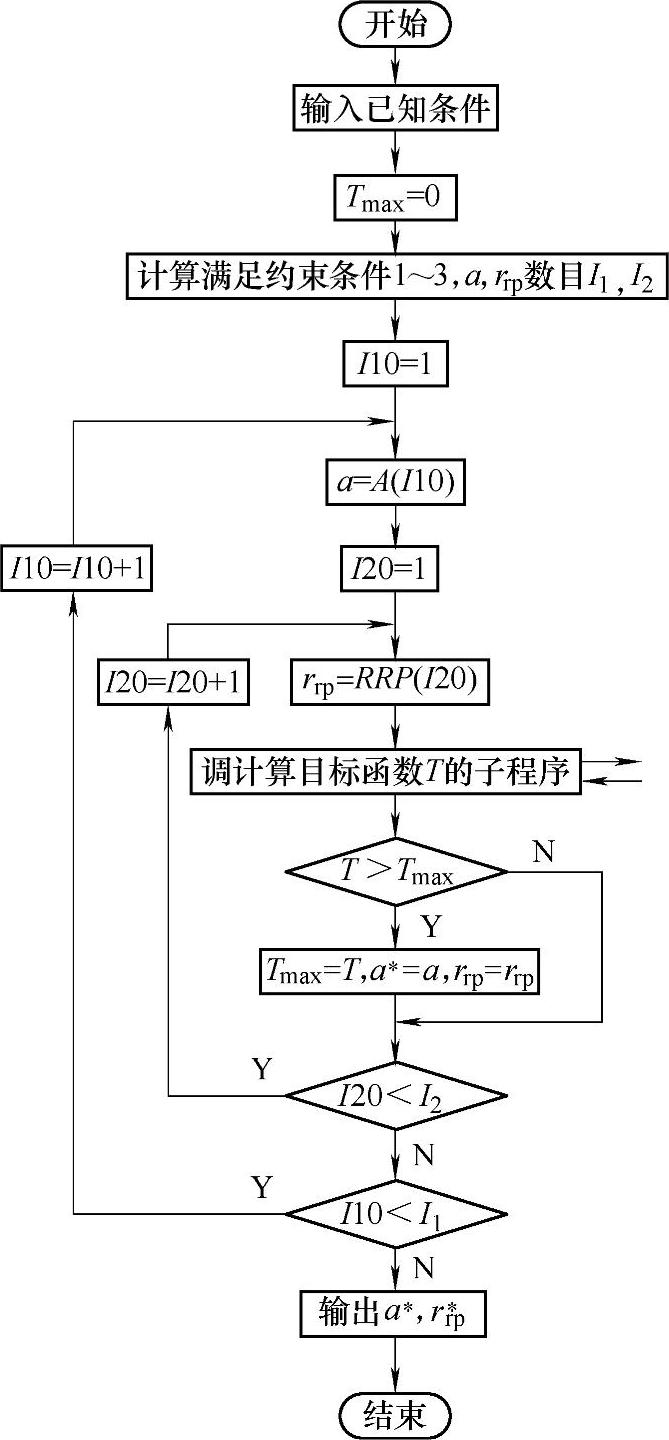
图11-38 a参数优化程序框图

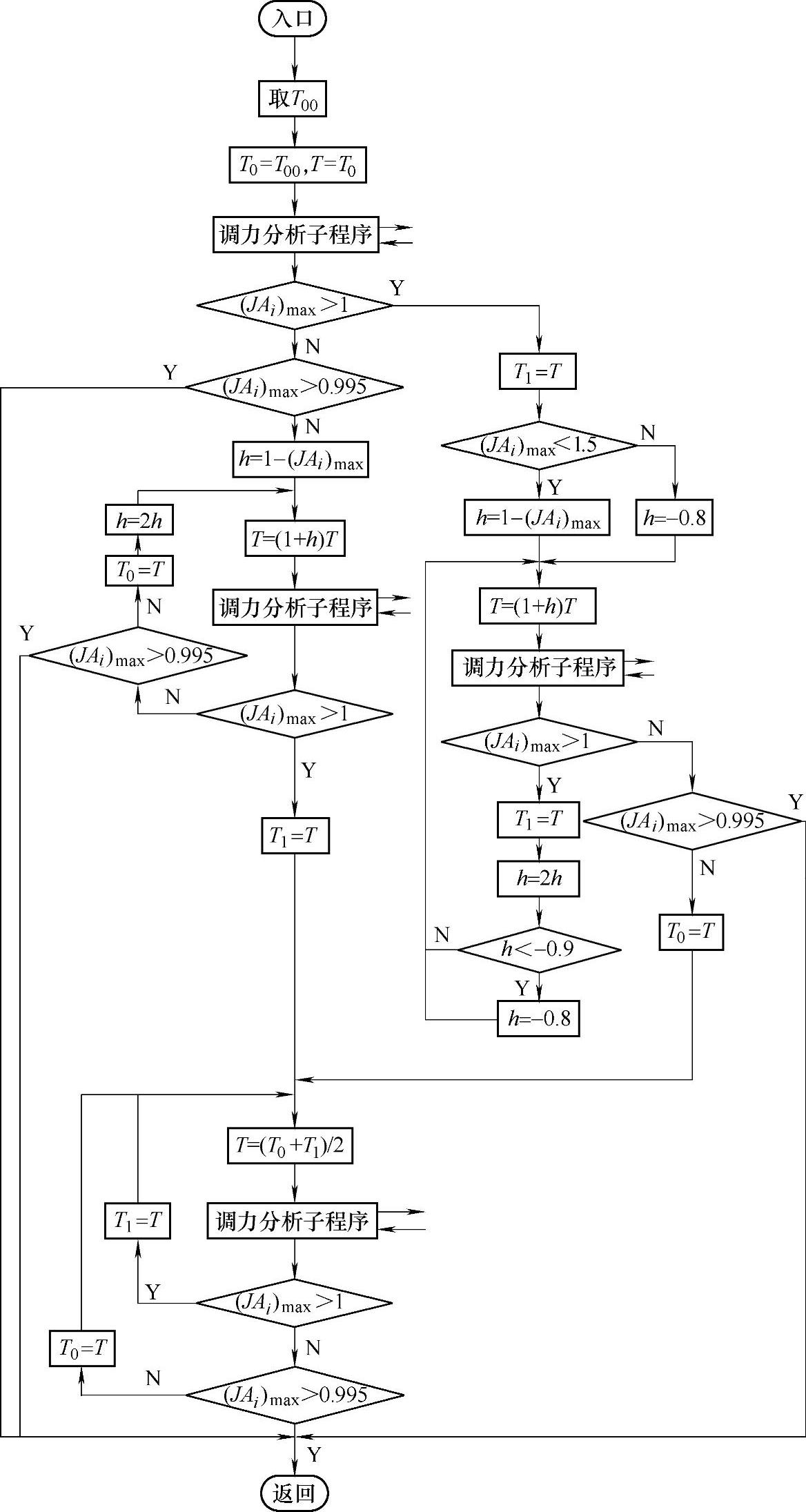
图11-38 b计算T子程序框图

②令T₀=T₀₀，取T=T₀+h×T₀（a式，h>0为步长）计算JA_i，若（JA_i）max仍小于0.995，则加大步长运用式（a）计算T，直到找出（JA_i）max≥0.995时的T值，若0.995≤（JA_i）max≤1，则该T值即为此点的目标函数值；若（JA_i）max＞1，则令T₁=T，再进行第4步。

③令T₁=T₀₀，取T=T₁-h×T₁（b式，h>0为步长）计算JA_i，若（JA_i）max仍大于1，则加大步长运用式（b）计算T，直到找出（JA_i）max≤1时的T值，若0.995≤（JA_i）max≤1，则该T值即为此点的目标函数值；若（JA_i）max<0.995，则令T₀=T，再进行第4步。

④此时T₀＜T，T₁＞T（T为该点的实际目标函数值）。运用等分法，取T=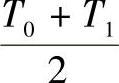[式（c）]，计算（JA_i）max，当（JA_i）max<0.995时，取T₀=T，再运用式（c）；当（JA_i）max>1时，取T₁=T，再运用式（c），直至达到0.995≤（JA_i）max≤1，此时的T即为该点的目标函数值。

程序框图见图11-38a。

计算目标函数T的子程序框图见图11-38b。

框图中力分析子程序的内容是，计算针齿受力齿数及受力分布情况，得出强度和轴承寿命等项指标，参考本章第4节。