前述标准齿形无隙啮合时，针齿与摆线轮齿啮合的作用力分析，由于未考虑摆线轮齿形修形的影响及轮齿接触变形与针齿销弯曲变形的影响，在实际工程计算中带来极大的误差（与实测F_max比较，有时误差达60%，甚至90%以上），因为经过齿形修形，无论是移距修形或等距修形，都会引起初始啮合间隙，使同时啮合有效传力的齿数减少，达不到针轮齿数的一半。

下面介绍考虑了摆线轮齿形修形及轮齿弹性变形影响，符合工程实际条件的较准确的力分析方法。

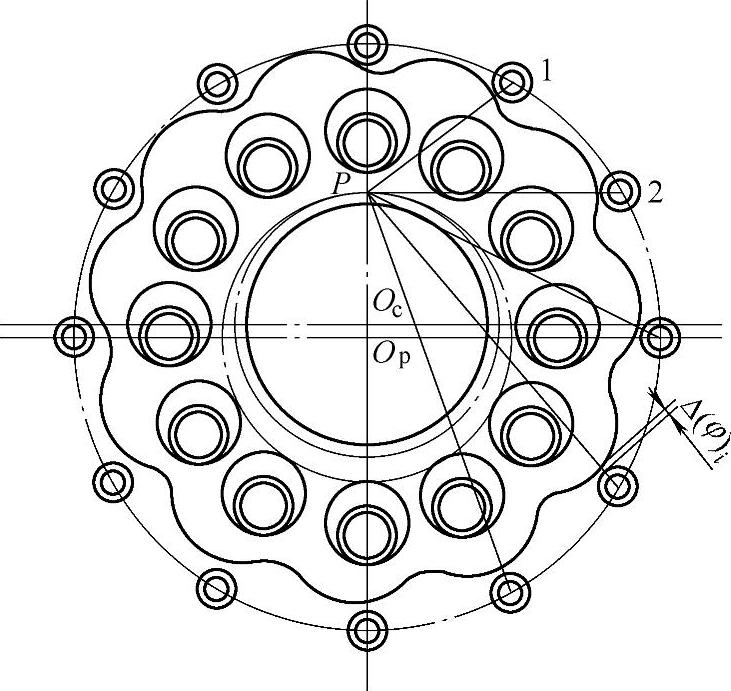
图11-30 因摆线轮修形引起的初始啮合侧隙

（1）初始法向啮合侧隙

标准的摆线轮以及只经过转角修形的摆线轮与标准的针轮啮合，在理论上都可达到同时啮合的齿数约为针轮齿数的一半，但摆线轮齿形只要经过等距、移距或等距加移距修形，如果不考虑零件弹性变形的补偿作用，则多齿同时啮合的条件便不再存在，而变为当某一个摆线轮齿和针轮齿接触时，其余的摆线轮齿与针轮齿之间都存在着大小各不相同的初始法向侧隙。参看图11-30第i对轮齿沿待啮合点（待啮合点是指齿形未修形前本应啮合，但由于齿形修形产生初始间隙而未啮合的点）法线方向的初始法向侧隙Δ（φ）i可按下式计算：

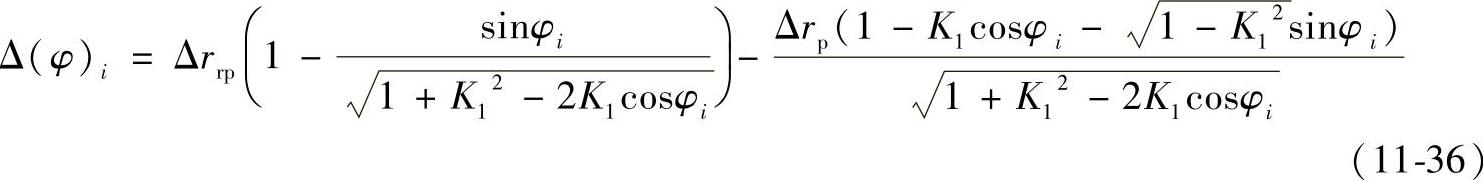
式中 φ_i——第i个针齿相对于转臂O_pO_c的转角（°）；

K₁——短幅系数，K₁=az_p/r_p；

其余符号同前。

令Δ（φ）i=0，由上式可解得

cosφ_i=K₁（a）

即φ_i=φ₀=arccosK₁（b）

这个解是使初始间隙为零的角度，空载时，只有在（或最靠近）φ₀=arccosK₁处的一对齿啮合。从φ_i=0到φ_i=180°的初始间隙分布曲线见图11-31中的实线。

（2）判定摆线轮与针轮同时啮合齿数的基本原理

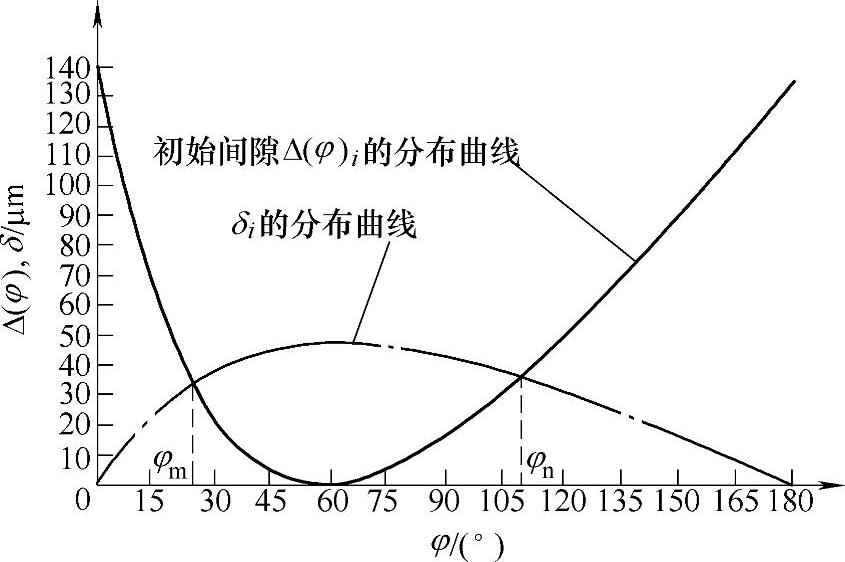
图11-31 Δ（φ）i与δ_i的分布曲线

见图11-28，设传递载荷时，对摆线轮所加转矩为T_c。在T_c的作用下，由于摆线轮与针轮齿的接触变形W及针齿销的弯曲变形f，摆线轮转过一个β角，若摆线轮体、安装针齿销的针齿壳和转臂的变形影响较小可忽略不计，则在摆线轮各啮合点公法线方向的总变形W+f或在待啮合点法线方向的位移应为

δ_i=l_iβ（i=1，2，…，z_p/2） （c）

式中 β——加载后，由于传力零件的变形所引起的摆线轮的转角（rad）；

l_i——第i个针齿啮合点的公法线或待啮合点的法线至摆线轮中心O_c的距离（mm）。

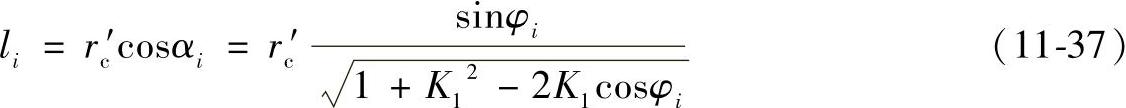
式中 r_c′——摆线轮的节圆半径（mm）；

α_i——第i个针齿啮合点的啮合角（°）；

其余符号意义同前。

设受力最大的一对摆线轮与针轮齿（即最靠近ϕ₀=arccosK₁处的一对齿）的接触变形w_max和针齿销的弯曲变形f_max的和为δ_max，其啮合点公法线至摆线轮中心O_c的距离为l_max，显然

式中

当受力最大的一对轮齿正好在φ₀=arccosK₁处时，无疑式（e）中l_max=r_c′；若只是很接近φ₀=arccosK₁处时，则为l_max≈r_c′。

联立式（11-37）及式（c）～式（e），并考虑到φ₀=arccosK₁，可得

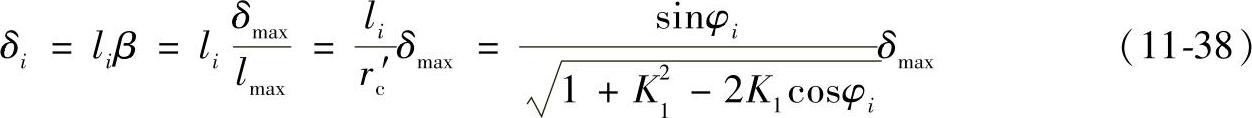
显然，在传递某一定转矩时，凡δ_i大于该位置初始间隙Δ（φ）i的各齿都将啮合，反之就不会进入啮合。δ₁的分布曲线可按式（11-38）计算结果画出如图11-31中的点划线。由点划线和实线（初始啮合间隙Δ（φ）i的分布曲线）的两个交点决定出两个对应的角度φ_m和φ_n，只有限定在φ_m和φ_n之间的各齿，才是真正进入啮合而同时受力的齿。

（3）确定摆线轮与针轮同时啮合传力齿数的原则

保证摆线针轮行星传动具有其优点的关键，在于保证合理的多齿啮合。合理范围的多齿啮合，其主要根据为以下两点：

1）应保证在区间〔φ_m，φ_n〕内，摆线轮至少有3～4个齿同时啮合传力，这是保证具有足够承载能力、传动平稳、噪声小、寿命长的最重要的条件。

2）区间的始位φ_m不宜过小，终位φ_n不宜过大。其主要原因（参看图11-28）是：①φ过小或过大处的轮齿传递转矩时，都是在压力角很大而力臂很小情况下传力，必然会造成传动效率下降；②φ_i角越大处的齿啮合时，啮合点K与瞬心P的距离KP也越大，从而在啮合处可能的滑动速度（等于摆线轮与针轮的相对角速度ω乘以啮合点K至瞬心P的距离）v=ωKP也越大，因此φ_i过大处的齿参加啮合，不论相对滑动速度是产生在针齿与摆线轮之间，还是产生在针齿套与针齿销之间，都会导致摩擦功率增大而传动效率降低；③φ_i角过大处的轮齿啮合，其当量曲率半径较小，即使受力小，接触应力σ_H并不小，当啮合处σ_H不小，而v却很大时，还可能导致胶合。通过对国内外一些摆线针轮行星减速器参数和性能的分析比较，推荐φ_m与φ_n的取值范围为：φ_m>25°；φ_n<100°。从保证基本承载能力又有较高传动效率的观点出发，同时啮合传力的齿数，既不能小于3～4个齿，也不宜过多。通常根据针轮齿数z_p的多少，在传递额定转矩时，将同时啮合有效传力的齿数控制在4～7个齿。

（4）修形齿形摆线轮与针轮啮合时的受力分析方法

1）确定摆线轮与针轮同时啮合的齿数z_T。对已设计好的摆线针轮行星减速器，可以按本节（2）中所述基本原理，根据传递的转矩、针齿结构尺寸及摆线轮的齿形修形量等已知条件进行计算，求得该减速器在传递给定转矩时同时啮合的齿数z_T。

对自行设计的摆线针轮行星传动，可按本节（3）中所述的原则，选定在传递额定转矩时啮合传力的齿数z_T，然后再按此设计针齿结构、尺寸和选定合理的摆线轮齿形修形量。

2）求同时啮合传力诸齿中受力最大齿所受之力F_max。修形齿摆线轮与针轮进行有隙啮合时，其主要特点有两方面：首先是摆线轮同时啮合传力的齿数不是约等于其齿数之半，而往往是z_T=3～7，若设计不合理或摆线轮齿形修形量选定不合理，可能出现z_T=1～2的非正常状态；另一方面是由于经过移距或等距修形的摆线轮在（或最接近）φ=arccosK₁处有一齿空载接触时，其余各齿与针轮齿，沿待啮合点的法线方向，均存在初始间隙Δ（φ）i（图11-30），且大小各不相同，特别是在修形量较大时差别极大。这时就不能再假定诸齿受力遵循F_i和δ_i=l_iβ成线性正比关系，只能假定F_i和δ_i-Δ（φ）i成线性正比关系。由于这一假定，科学地考虑了能起主要作用的初始间隙Δ（φ）i及受力零件弹性变形的影响，因而用于工程上进行力分析是足够准确的。

按此假定，在同时啮合传力的z_T个齿中的第i齿受力F_i可用下式表示：

式中 F_max——在（或接近于）φ_i=φ₀=arccosK₁处（亦即在或接近于l_i=l_max=r′_c的针齿处）的齿最先接触受力，显然在同时受力的诸对齿中，这对齿受力最大。故以F_max表示该对齿的受力（N）。

其余各符号含义同前。

设摆线轮上的转矩T_c由i=m至i=n的z_T个齿传递，由力矩平衡条件可得

将式（11-39）代入式（f），同时考虑到δ_max=r′_cβ及δ_i=l_iβ，可得

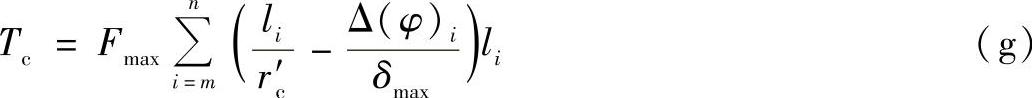
由式（g）即可得到同时传力诸齿中受力最大齿所受力Fmax

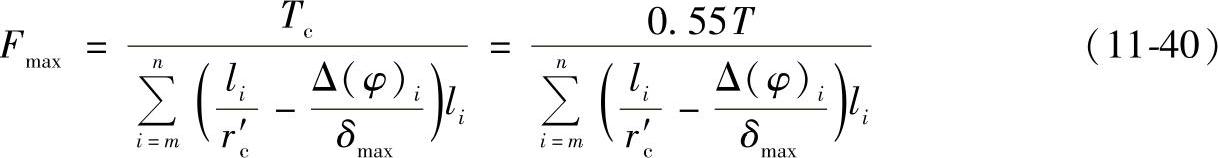
式中 T——输出轴上作用的转矩（N·mm）；

l_i——第i齿接触点的公法线到摆线轮中心O_c的距离（mm），可按式（11-37）计算；

r′_c——摆线轮的节圆半径（mm），r′_c=az_c；

Δ（φ）i——第i齿处的初始间隙（mm），可按式（11-36）计算；

δ_max——在φ=arccosK₁处，受力最大的一对齿（摆线轮齿与针轮齿）在F_max作用下，在接触点公法线方向的总的接触变形w_max与针齿销弯曲变形f_max的总和（mm）

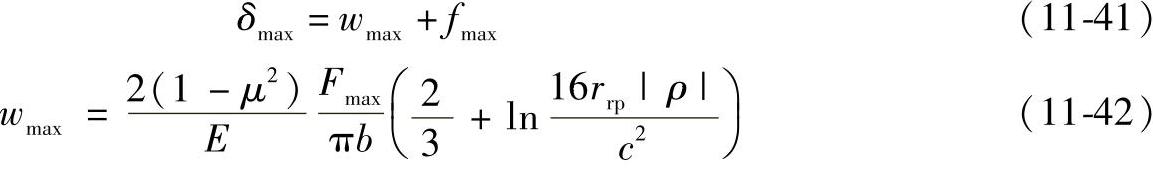
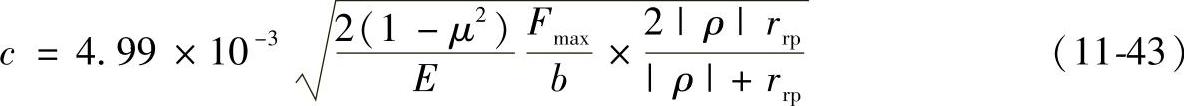(www.daowen.com)

式中 _μ——摆线轮与针轮齿材料的泊松比，二者材料相同均为GCr15，μ=0.3；

E——摆线轮与针轮齿材料的弹性模量（MPa），二者材料均为GCr15，E=2.06×10⁵MPa；

ρ——摆线轮在φ=φ₀=arccosK₁处的齿廓曲率半径（mm），由式（11-12）可得

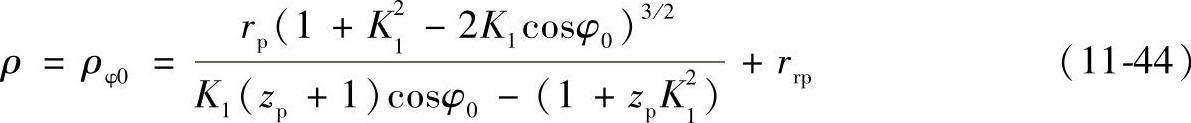
此处ρ=ρφ0为正时表示该处齿廓内凹，ρφ0为负时表示该处外凸。由于φ₀=arccosK₁值恒大于摆线轮齿廓曲线拐点处的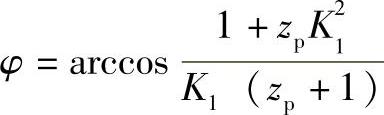值，也就

是说在φ=φ₀处，齿廓恒为外凸，因而计算出之ρφ0值应恒为负值；

f_max——针齿销在F_max作用下，在力作用点处的弯曲变形（mm），精确计算须用有限单元法，简化计算可按图11-32所示的针齿销受力简图进行计算。

当针齿销为两支点（图11-32a）时

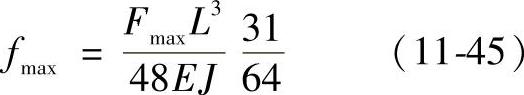
当针齿销为三支点（图11-32b）时

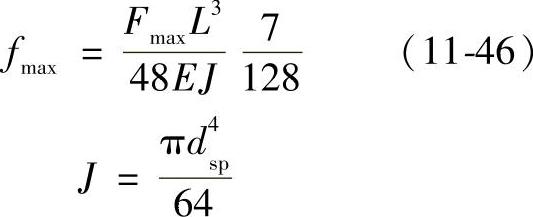
用式（11-40）计算F_max时，需要知道δ_max及起始啮合齿号m、终了啮合齿号n，而用式（11-41）～式（11-46）求δ_max时又需知F_max。实际计算时要先给出一个F_max的初始值F_max0代入式（11-41）～式（11-46）求出δ_max的初始值δ_max0再按（2）节所述判定摆线轮与针轮同时啮合齿数的基本原理，判断起始啮合齿号和终了啮合齿号，再将δ_max0反过来代入式（11-40）求出第一次迭代的结果F_max1。比较F_max1与F_max0，若Fmax1与Fmax0之差的绝对值大于0.1%F_max1，就将F_max1代入式（11-41）～式（11-46）求δ_max1，将后者再代入式（11-40）求出第二次迭代的结果F_max2。按此方式多次反复迭代，直到第k次迭代所得到的F_maxk满足F_maxk^-Fmax（k-1）<0.1%Fmaxk，然后取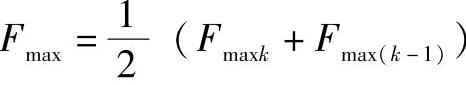即为准确的F_max值。

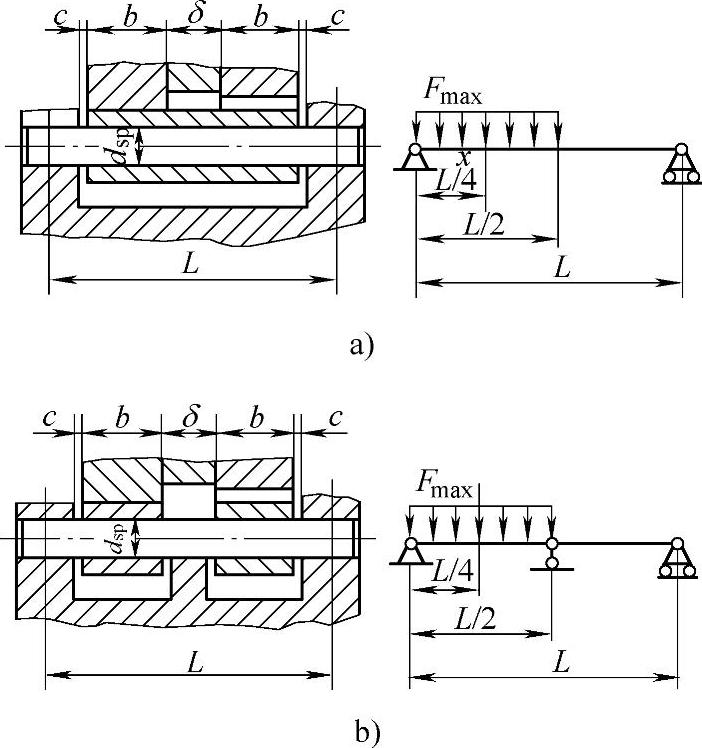
图11-32 针齿销受力简图

a）两支点的针齿 b）三支点的针齿

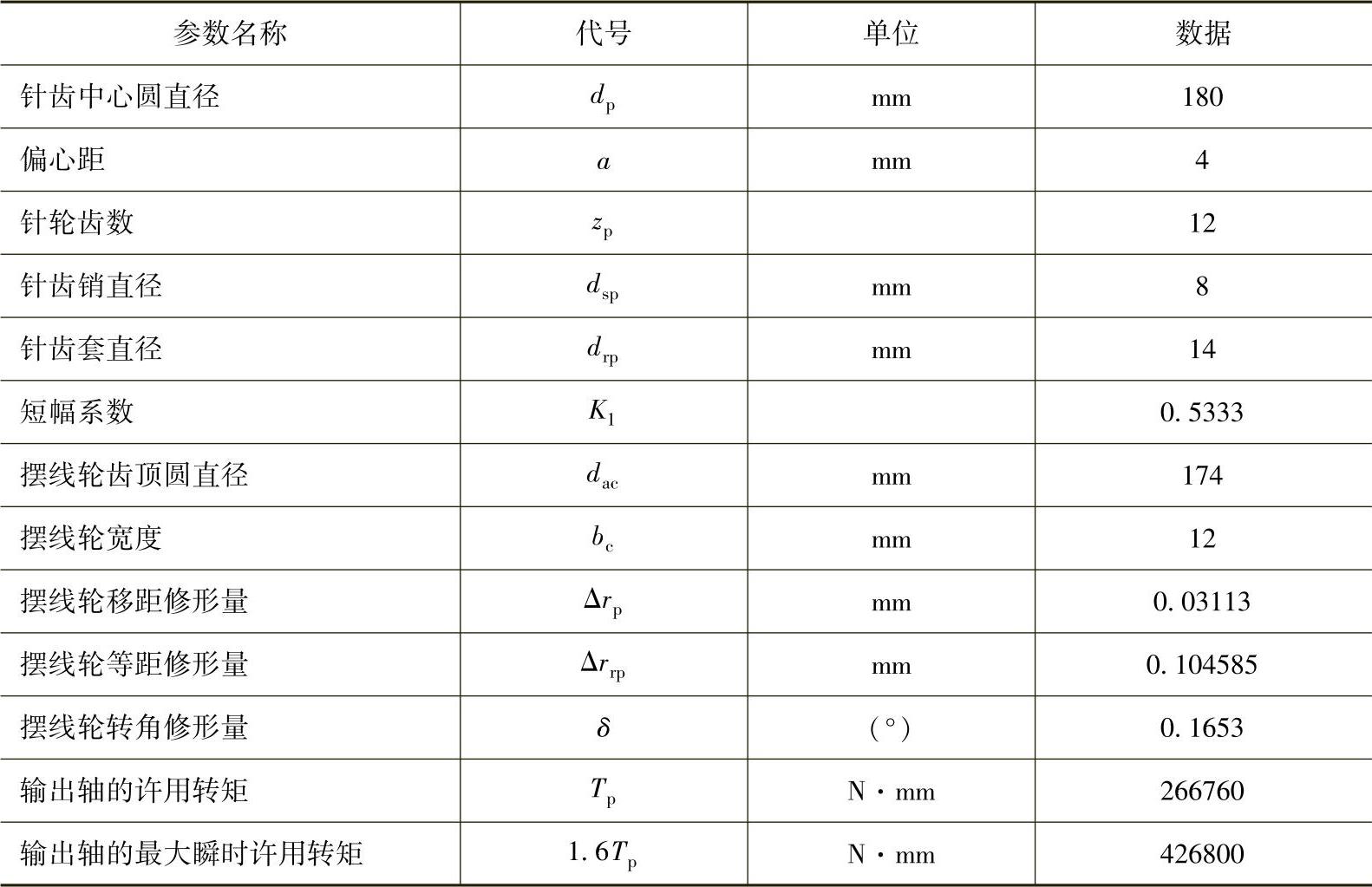
例11-3 已知BW180摆线针轮行星减速器有关参数见表11-10。

求此减速器中修形齿摆线轮与标准针轮啮合，传递输出轴的最大瞬时许用转矩时，同时啮合传力的齿数，作用在受力最大齿上的最大作用力F_max。

表11-10 BW180摆线针轮行星减速器参数

解

（1）计算初始啮合间隙

当摆线轮齿兼有等距修形与移距修形时，各对轮齿沿待啮合点法线方向的初始间隙，可按式（11-36）计算，结果列于表11-11。初始间隙的分布曲线如图11-31所示，以实线表示。

（2）判定摆线轮与针轮同时啮合的齿数

由表11-10知，输出轴的最大瞬时许用转矩为

T=1.6T_p=1.6×266760 N·mm=426800 N·mm

在标准齿形摆线轮与针轮处于理论上的无隙啮合时，同时啮合的齿数约为针轮齿数的一半，如图11-28，共有5个。其中受力最大的齿为2#齿（该齿处于φ_i=60°，最接近于φ₀=arccosK₁=57°46′）。所受力F′_max可按式（11-35）算出为

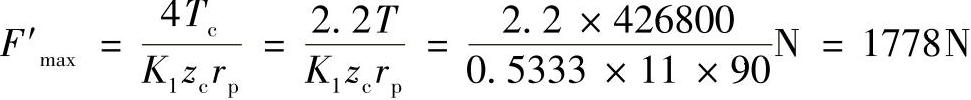
若摆线轮齿形经过修正，与针轮处于有隙啮合状态，并且在φ₀≈arccosK₁处只一对齿啮合时，则作用力可按下式计算：

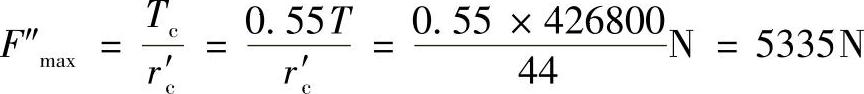
在本例中，F″_max∶F′_max=3∶1

表11-11 初始啮合间隙计算结果

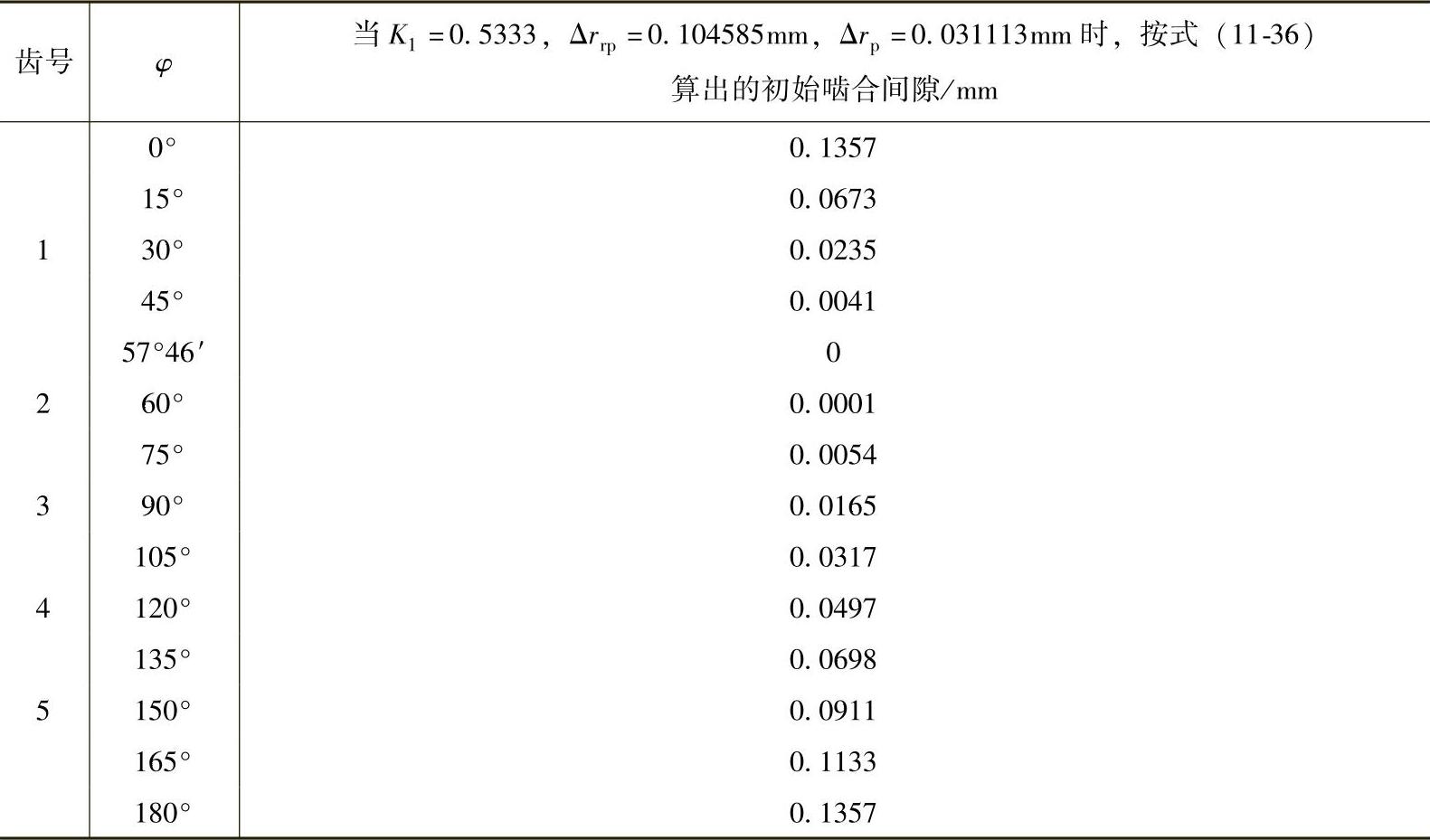
利用式（11-41）～式（11-46），分别求出F′_max与F″_max作用时，受力最大的这对齿在接触点公法线方向的总的接触变形w_max与针齿销在受力点的弯曲弯形f_max的总和各为

δ′_max=w′_max+f′_max=（0.00533+0.022）mm=0.02733mm

δ″_max=w″_max+f″_max=（0.01462+0.066）mm=0.08052mm

按式（11-38），分别算出由δ_m′_ax与δ″_max引起的摆线轮其他各齿沿接触点公法线或待啮合点法线方向位移δ′_i与δ″_i列于表11-12。

表11-12 δ′_i与δ″_i的计算

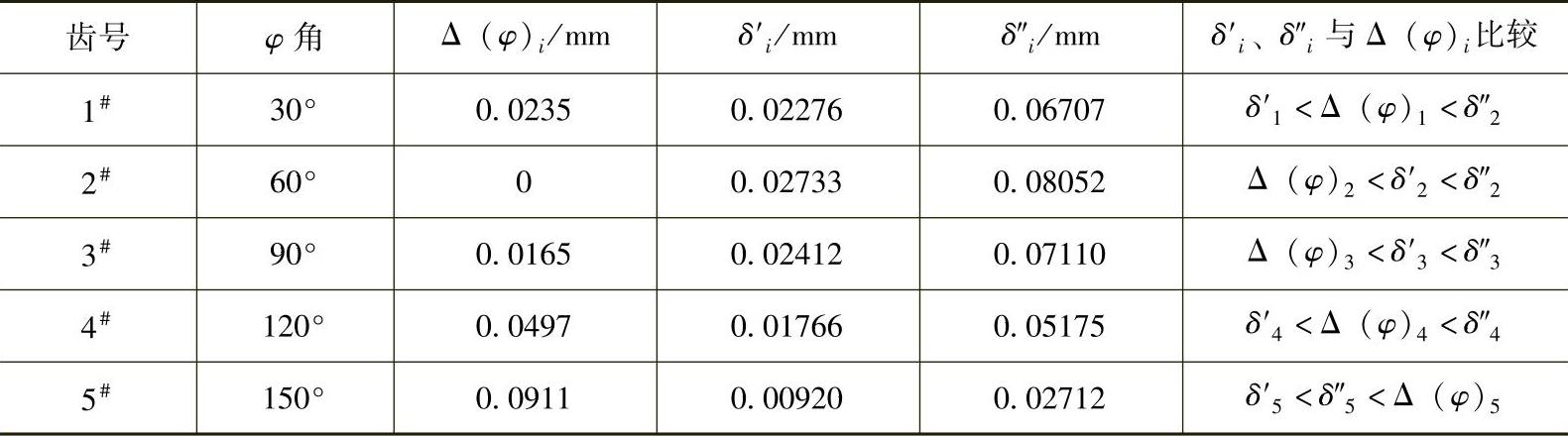
由表11-12可知，当δ′_max=0.02733mm。只有2#与3#齿满足Δ（φ）i<δ′_i条件，这说明按5对齿同时啮合来计算F′_max不符实际。

由表11-12还可知，当δ″_max=0.08052mm时，将有1#、2#、3#、4#共4齿满足Δ（φ）i<δ″_i条件，这说明按摆线轮只一齿啮合传力来算F″_max也不符合实际。

由表11-12还可看出，由于初始间隙Δ（φ）4=0.0497mm比较大，假定摆线轮有4齿同时啮合传力，则F_max必将远小于只一齿传力时的F″_max，这要满足δ₄＞Δ（φ）4显然不可能。

综合上述，可以判定在本例中，摆线轮是3个齿同时啮合传力。

（3）修形齿形摆线轮与针轮啮合时的受力分析

由于实际的F_max必在F′_max与F″_max之间，故取二者之平均值，作为用迭代逐次逼近法，求F_max时的初始值Fmax0

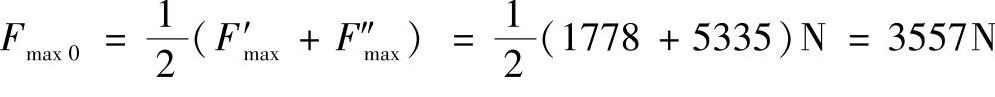
以之代入式（11-41）～式（11-46），求得

δ_max0=0.0543 mm

再以δ_max0之值代入式（11-40）求出

F_max1=2902N

因|F_max1-Fmax0|=655N>0.1%F_max1。应继续进行迭代逼近计算。迭代计算的中间及最后结果列于表11-13。由表11-13可知，只经过8次迭代计算，即得到准确的结果Fmax。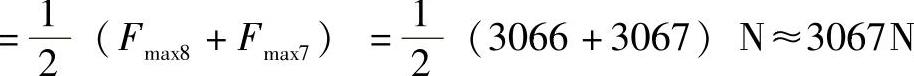

表11-13 迭代法计算F_max之结果

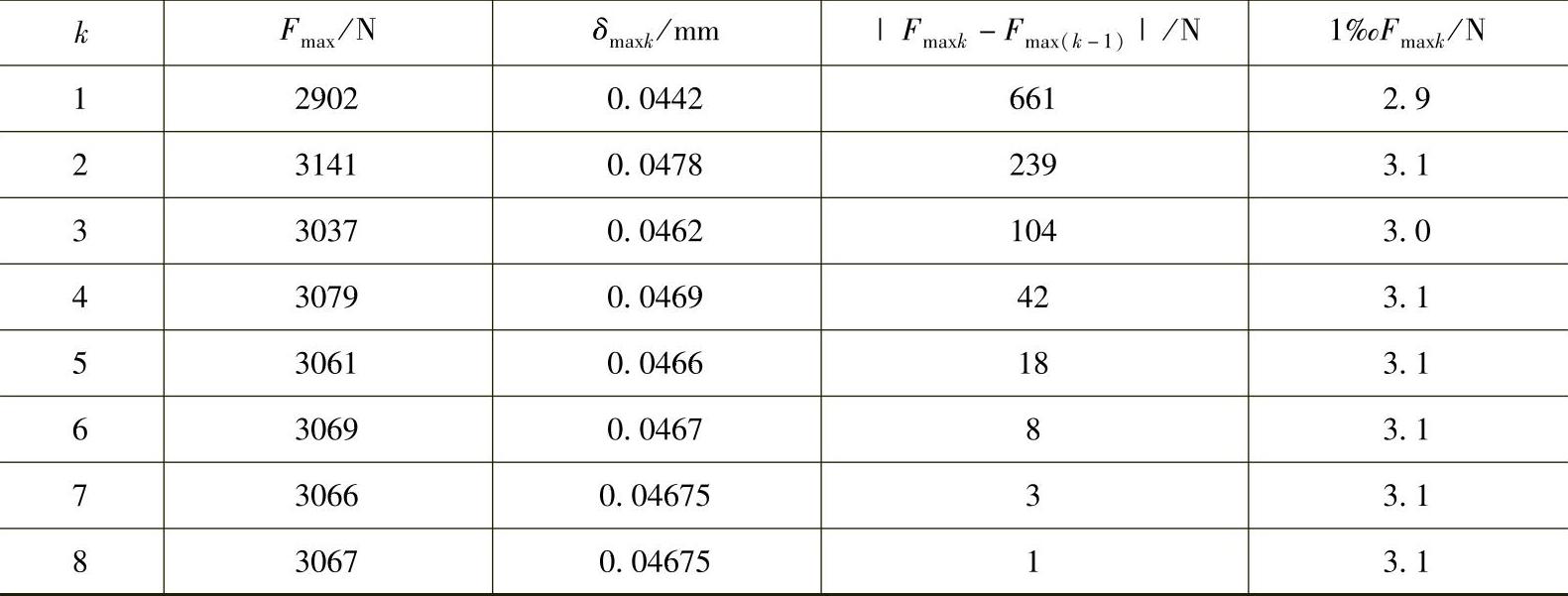
通常，上述用反复迭代方法求F_max的工作均采用排好的程序在计算机上进行计算。其程序框图见图11-33。

以上计算实例是按针齿中心圆直径正好为公称尺寸d_p=180mm进行计算的，若实际针齿中心圆直径为d_p+Δd_p，实际增大的Δd_p部分对初始啮合间隙Δ（φ）i的影响将相当于移距修形量Δr_p减少了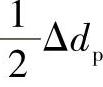。因此，这时在上例中计算Δ（φ）i公式中的Δr_p值就应当以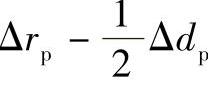值代入。同样，若实际针齿直径为d_rp+Δd_rp，实际增大的部分Δd_rp对初始啮合间隙Δ（φ）i的影响相当于等距修形量Δr_rp减小了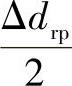。因此，计算Δ（φ）i公式中的Δr_rp值应以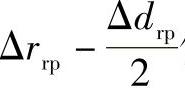值代入。

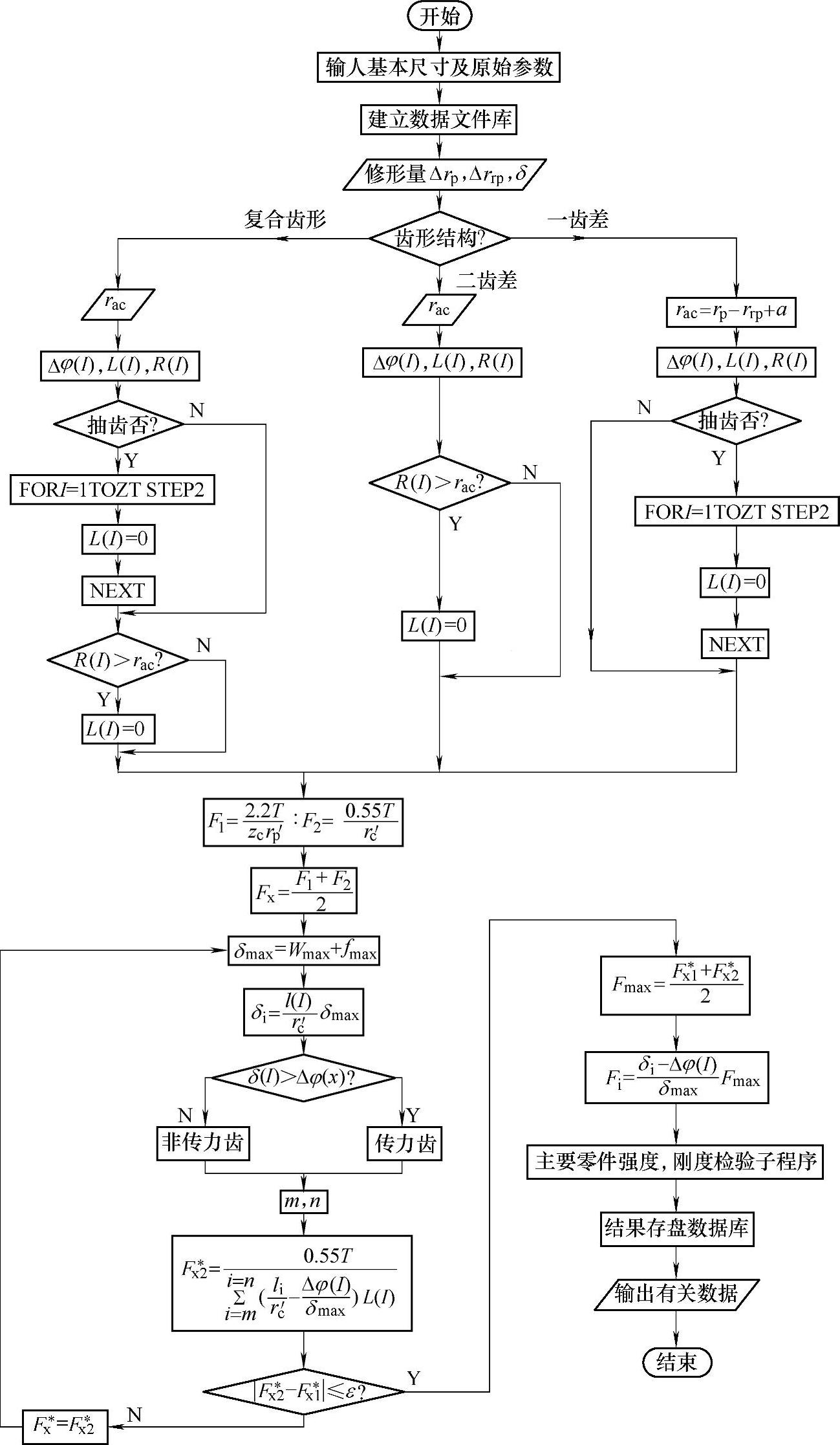
图11-33 摆线轮齿受力分析程序框图