如假设针轮固定不动，对摆线轮（行星轮）加一转矩T_c，在T_c的作用下，由于传力零件的弹性变形，摆线轮转过一个β角。如果摆线轮体、针齿套和转臂的变形忽略不计，求得针齿销的弯曲和轮齿接触挤压的总变形，对针齿2、3、4、…（图11-28）分别为

δ₂=l₂β；δ₃=l₃β；…

摆线轮齿廓与针齿齿廓在接触处的公法线（即接触处的受力线F_i）与节点的圆周速度方向所夹的锐角（α_i）称为啮合角，可见，摆线轮齿和针轮齿在不同啮合位置啮合时，其啮合角不相等，见图11_-28。

假定针齿承受的载荷F₂、F₃、F₄、…和相应的变形l₂β、l₃β、l₄β、…成线性关系。由于和不同的针齿啮合时，因当量曲率变化引起的非线性对于我们所取的δ和l之间的关系只引起很小的偏差，所以上述假设是允许的。

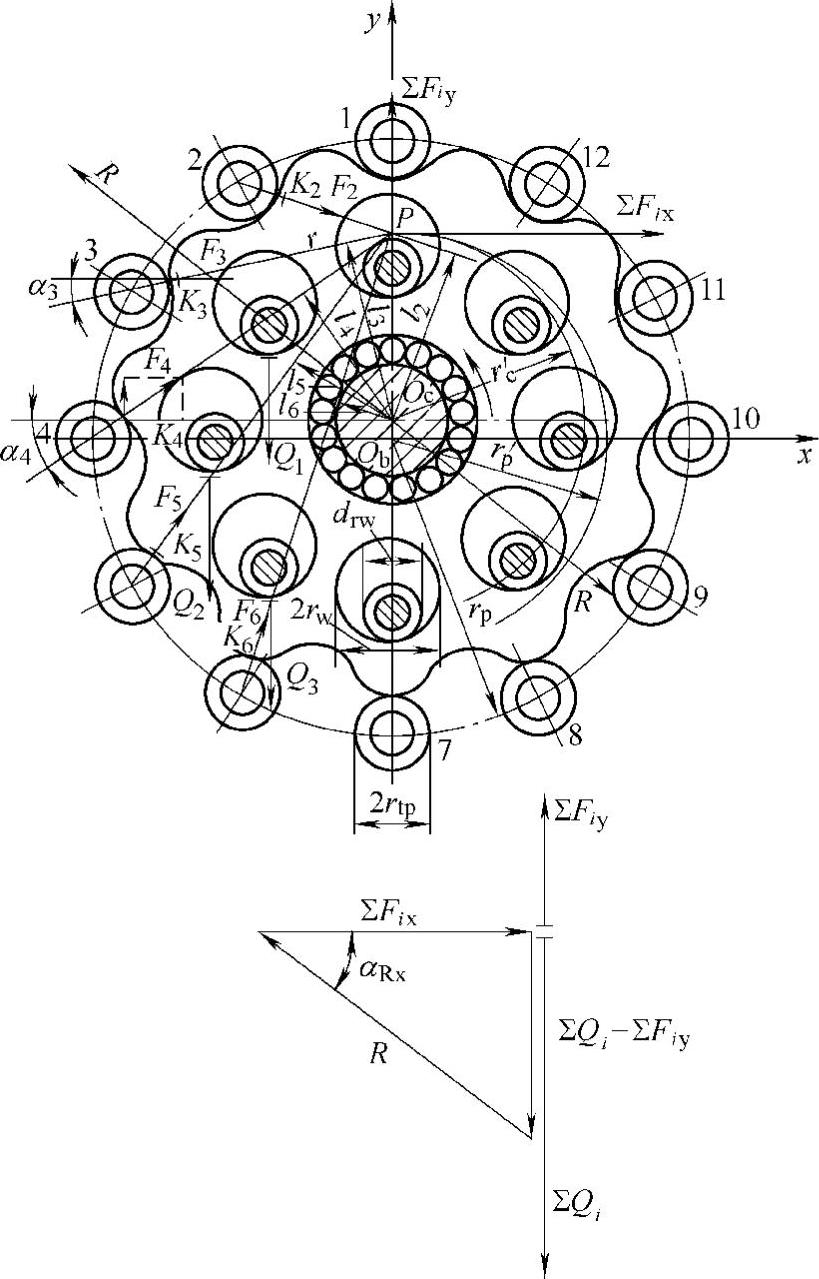
图11-28 摆线轮受力分析图

最大载荷F_max是在最大力臂l_max=r′_c的针齿处（图11-29）。作用在第i个针齿上的力用下式确定：

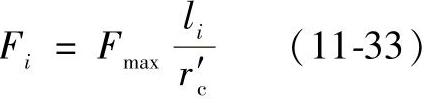
由摆线轮传递的转矩为T_c，得

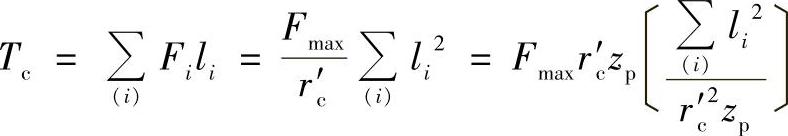(www.daowen.com)

式中方括号中的值为常数，等于0.25，故得

或写为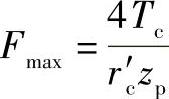

考虑到r′_cz_p=r′_pz_c=K₁r_pz_c代入上式得

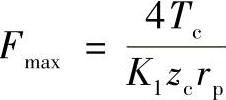
由于制造误差，传给两个摆线轮的转矩是不相等的，即其中之一的T_c值略超过0.5T（T为输出轴传递的总转矩）。故在力分析与强度计算时，建议取T_c=0.55T，代入上式得

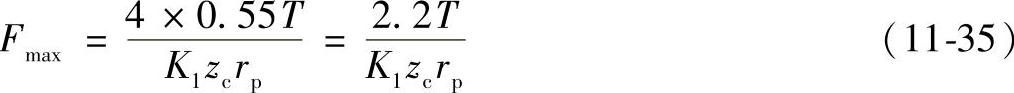
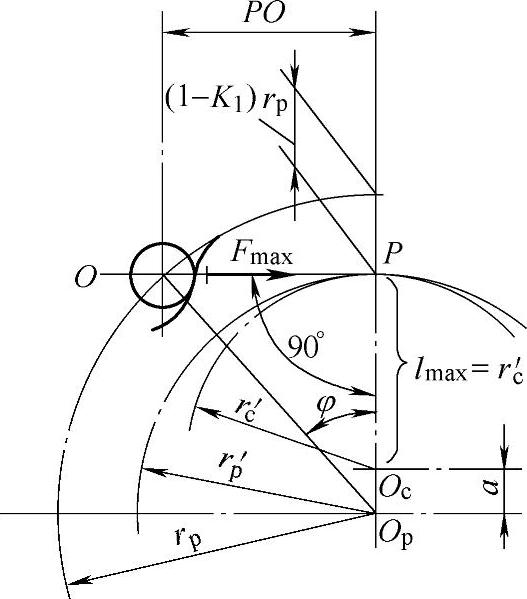
图11-29 承受最大载荷F_max的针齿位置