摆线针轮行星传动是以r_p、b_c、z_p作为基本参数，将其他各参数尽可能化为r_p、b_c及z_p的函数，这样可有利于分析设计参数对性能指标的影响。为此，须引用以下两个系数：

（1）短幅系数K₁

在本章第2节讨论摆线针轮行星传动的啮合原理时，已经引出了短幅系数K1

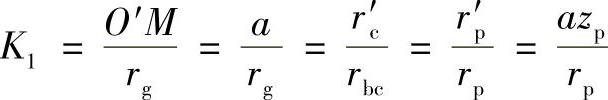
K₁的取值不同，摆线轮的齿形就不同，会影响传动的性能指标，所以是一个很重要的系数。K₁取值既不宜过大也不能过小。

1）K₁不能过大的原因 由式（11-11）及作为实例的图11-24可知，K₁过大（例如K₁≥0.9）时不仅摆线轮齿廓外凸部分远大于内凹部分，而且外凸部分的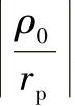又较小，要想在整个接触区满足r_rp＜|ρ₀|_min，则r_rp就只能选用得较小，这就使当量曲率半径小而导致工作时接触应力增大。此外，K₁过大则偏心距a=K₁r_p/z_p在传动比较小从而z_p较小时就会过大，这会为设计合理的W机构造成困难。见图11-25a，当传动比较小（i=11），而K₁=0.9时，虽然柱销孔半径r_w尽可能取大，柱销套半径r_rw=r_w-a会仍很小，而柱销半径r_sw更小，用这样细的柱销传动，会严重影响整机传递转矩的能力。

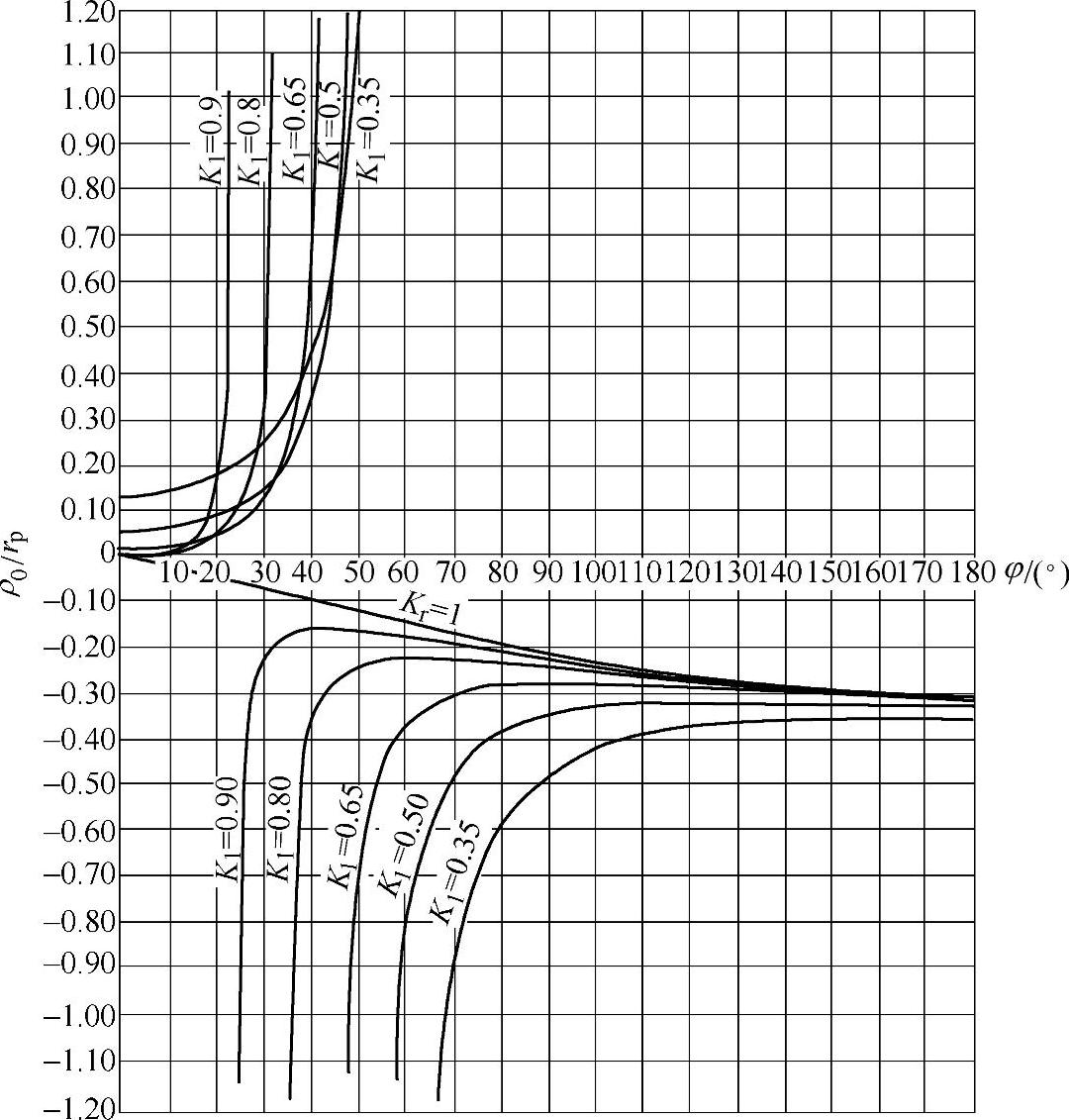
图11-24 z_c=11和z_p=12各种K₁值时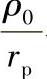与φ之间的关系

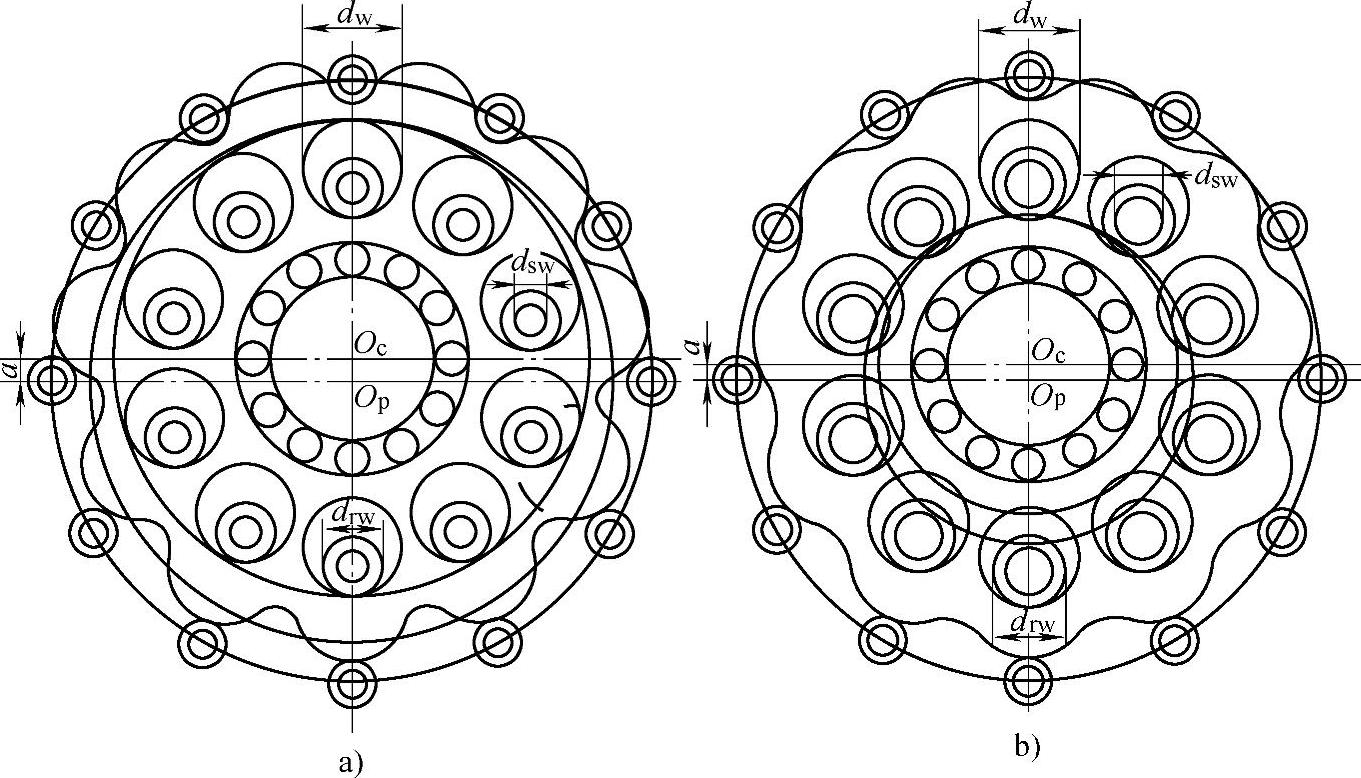
图11-25 z_p=12选择K₁值对W机构设计的影响

a）K₁=0.9的传动 b）K₁=0.5333的传动

2）K₁不能过小的原因K₁过小则摆线轮的节圆半径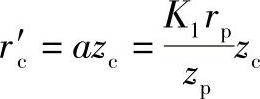和针轮的节圆半径r_p′=K₁r_p都随之显著缩小，因而节点P与摆线轮中心O_c的距离也显著缩小，在传递转矩一定的条件下，各针齿和摆线轮的啮合作用力（均通过节点P）就会因力臂减小而增大。例如，在z_c=11、z_p=12、r_rp=0.1r_p的传动中，当K₁=0.28，其能传递的转矩仅为K₁=0.5333时的60%。(www.daowen.com)

由上可知，K₁接近1不好，K₁比1小得过多也不好。比较合理的K₁值应通过整机优化设计来确定，其推荐值列于表11-3。

表11 - 3 短幅系数K₁推荐值

（2）针径系数K₂

针轮上相邻两针齿中心之间的距离与针齿套直径的比值称为针径系数，用K₂表示。针径系数K₂的大小表明针齿在针轮上的分布密集程度。如图11-26有

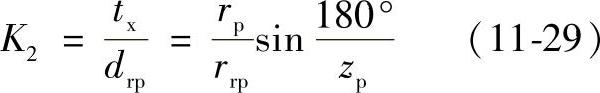
为避免针齿相碰和保证针齿与针齿壳的强度，可取K₂=1～4，以K₂=1.5～2.0为最佳，一般不小于1.25～1.4。当z_p≥44时，为避免针齿相碰，若将针轮齿数抽去一半，可取K₂≥0.99～1.0。设计时，K₂值可参考表11-4选择。

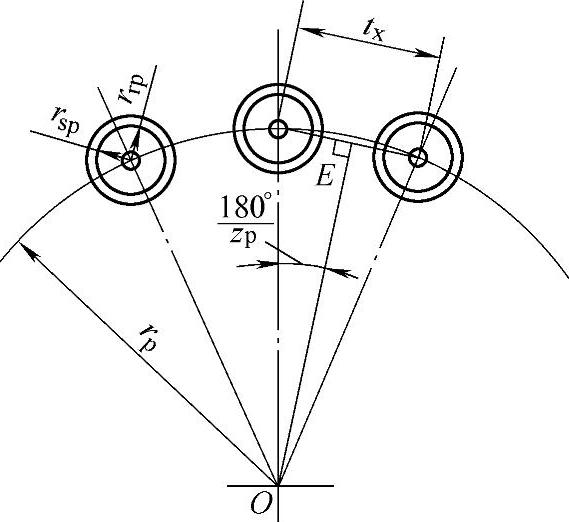
图11-26 针径系数K2

表11 - 4 针径系数K₂推荐值