如图11-19所示，由于“二齿差”传动中摆线轮的齿形是由两条相位相差半个周节的“一齿差”摆线轮齿形相交而形成，故其齿顶为一尖点。由于尖点使齿廓顶部强度不足，还会在传动中引起噪声，因此需要优选一条与齿形工作部分圆滑相连的修顶曲线修去齿顶尖点。

（1）未修顶时齿顶圆半径的计算

见图11-20，两条短幅外摆线的等距曲线的交点A就构成了二齿差摆线轮的齿顶。

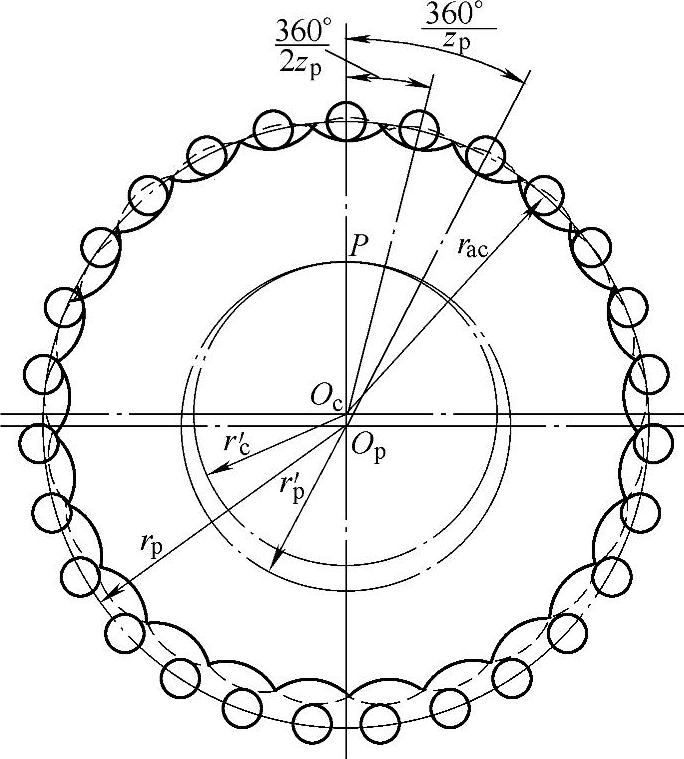
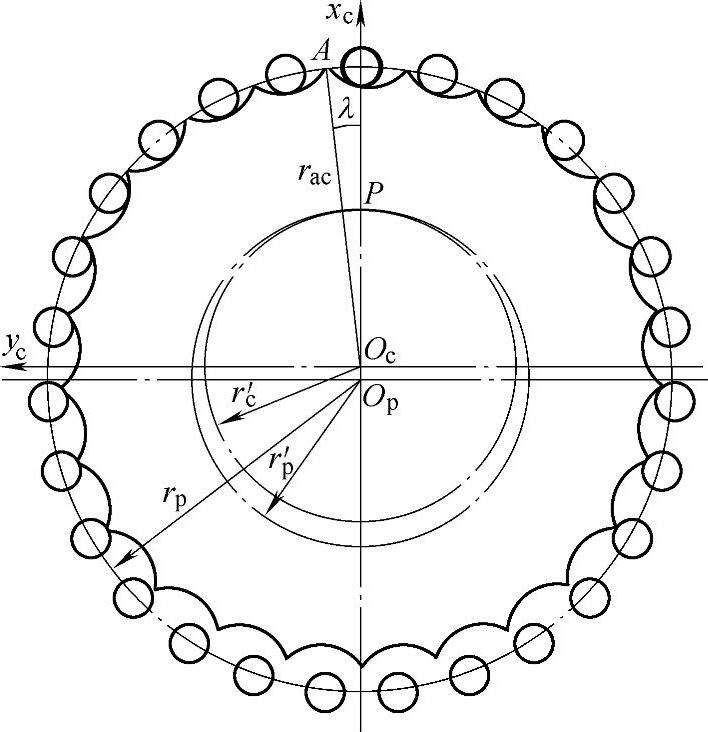
图11-20 二齿差传动齿顶圆计算

由图11-20知

图11-19 二齿差摆线针轮行星传动

显然，设A点坐标为（x_A，y_A），则

又由通用的摆线轮齿形方程式（11-9）可得：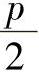

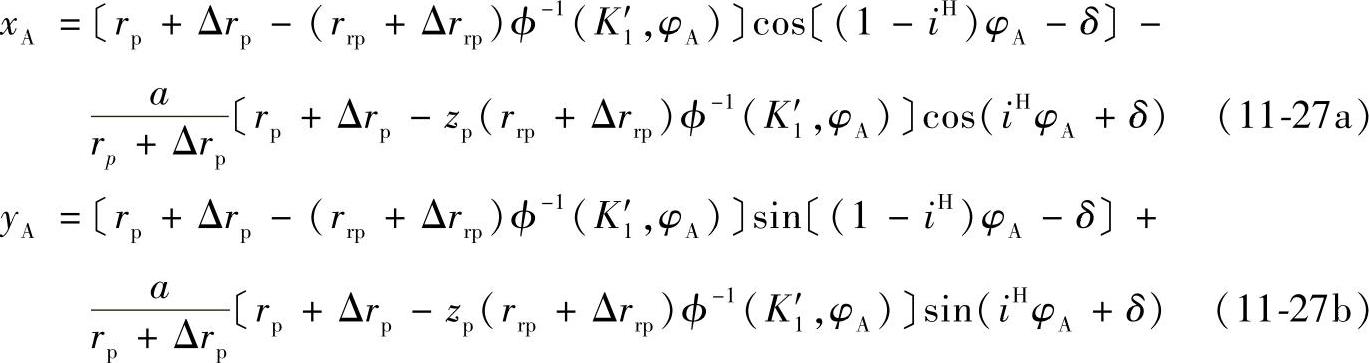
已知r_p、r_rp、a、z_p=z′_p/2（z′_p为二齿差传动针轮的实际齿数）、Δr_p、Δr_rp、δ，由式（11-25）算得λ值，将式（11-26）、式（11-27a）、式（11-27b）三式联立，用计算机求解，就可求出φ_A、x_A、y_A的数值。从而未修顶时齿顶圆的半径

（2）修顶曲线参数的选择

比较实用的修顶方法是优选另一条短幅外摆线的等距曲线作为“二齿差”传动摆线轮的修顶曲线，如图11-21所示，曲线MAN是二齿差传动摆线轮修顶前的齿廓，曲线EKK′F是优选出来的另一条短幅外摆线的等距曲线，它与前一曲线MAN相交于K、K′两点，二条曲线在交点切线的夹角很小。显然，若用短幅外摆线的等距曲线EKK′F的KK′段修去原二齿差传动摆线轮的齿尖，而作为摆线轮的顶部曲线，则在展成法摆线磨齿机上是很容易实现的理想修顶曲线。

优选修顶用的短幅外摆线的等距曲线EKK′F参数的方法与本章前面2.4节所述优选复合齿形顶部曲线参数的方法基本相同。应注意的要点如下：

1）为使修顶曲线与原二齿差工作齿廓相连处（图11-21中的K与K′点处）较光滑的过渡，在优选修顶曲线时，可采用复合齿形优选顶部曲线相同的方法，把两条短幅外摆线的等距曲线交点K处的切线夹角作为目标函数F，使其极小化。通常要求在交点的两切线夹角不大于6°。

2）为在展成法摆线磨齿机上一次修完所有齿顶，修顶短幅外摆线的等距曲线参数摆线齿数z_c2通常应选为二齿差摆线轮实际齿数z′_c的2倍或3倍。

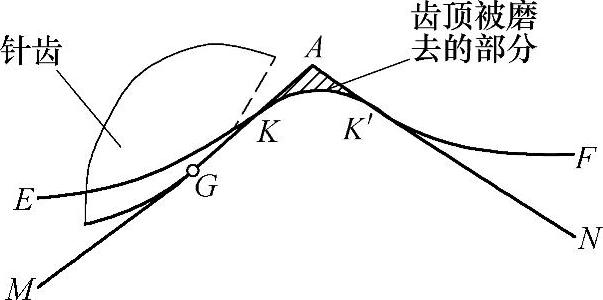
图11-21 二齿差传动摆线轮的修顶曲线(www.daowen.com)

3）修顶曲线的偏心距a₂应符合摆线磨齿机的偏心距系列（单位mm），通常可在0.75、1.0、1.25、1.5及1.75这几个数值中按a值大小选。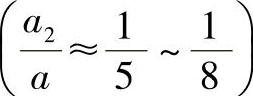

4）为使磨齿砂轮有合理寿命，修顶曲线参数中的针齿半径r_rp2不应过小，通常可取

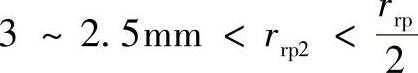
5）修顶曲线不得产生顶切，其约束条件为

g₁（x）=r_rp2-|ρ₀|_min＜0

式中 |ρ₀|_min——修顶短幅外摆线的等距曲线的理论齿廓的最小曲率半径，其计算见式（11-17）及表11-1中的式（11-15）与式（11-16）。

6）修顶曲线的起始点K应在有效传力轮齿的最远啮合点（如图11-21中的G点）之外，以保证有足够的同时啮合传力的齿数，通常设计时，应争取有4、5个齿同时啮合传力。设对应于啮合点最远的针齿相对于转臂的转角（啮合相位角）为φ_G，而摆线轮工作齿廓与修顶曲线交点K处的啮合相位角为φ_K，则上述要求可写为如下的约束条件：

g₂（x）=φ_G-φ_K＜0

7）在修顶起始点K（图11-21）以前，二齿差传动摆线轮的工作齿廓MK不得与修顶曲线相交，以保证工作齿廓MK的正确齿形。此点可写为约束条件：

g₃（x）=x（y）-x₂（y）＜0

式中 x（y）、x₂（y）——对应相同y坐标的工作齿廓的x坐标和修顶曲线的x坐标。

根据上述目标函数和约束条件搜寻修顶曲线参数的优化设计程序框图见图11-22。

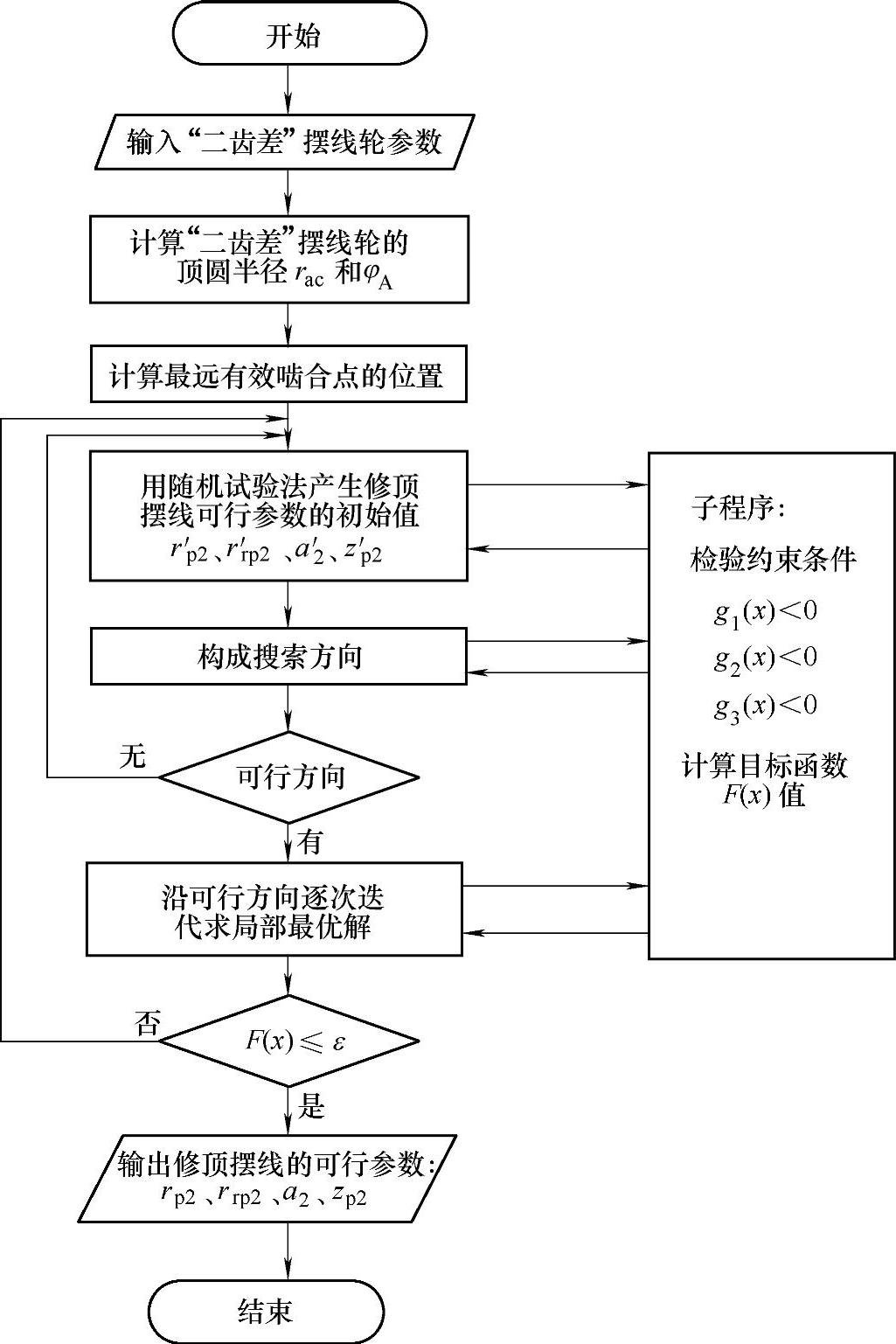
图11-22 求修顶曲线参数的计算机程序框图

例11 - 2 二齿差传动的摆线轮参数为r_p=109mm，a=5mm，r_rp=8.5mm，z_p=12，z′_p=24，Δr_p=0.569mm，Δr_rp=0.719mm，δ=0°，设计修顶曲线。

解 用上述方法，按图11-22的优化设计程序框图，优选出修顶曲线的诸参数为：r_p2=105mm，r_rp2=4.35mm，a₂=0.75mm，z_p2=67。用此参数，工作齿廓与修顶曲线在交点K切线的夹角只有2.26°，连接很光滑，同时啮合传力齿数为4。修顶前的齿顶圆半径r_ac=101.787mm，修顶后的齿顶圆半径为r_ac2=101.4mm，二曲线交点K处矢径长r_K=101.021mm，见图11-23。

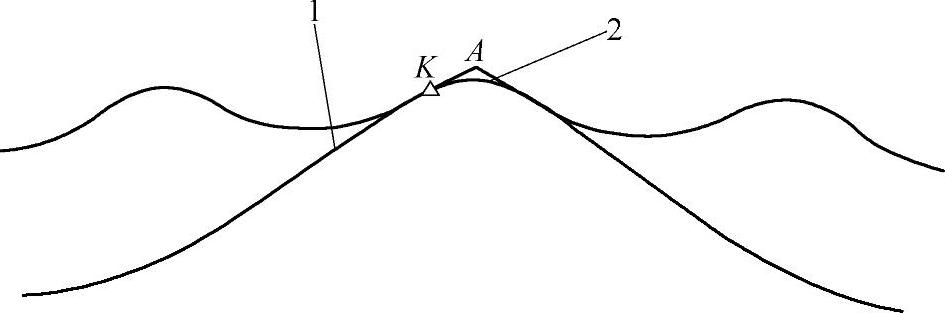
图11-23 二齿差传动摆线轮修顶实例图

1—工作齿形部分，其参数：r_p=109mm a=5mm r_rp=8.5mm z_p=12 Δr_rp=0.719mm Δr_p=0.569mm

2—修顶曲线，其参数：r_p2=105mm r_rp2=4.35mm a₂=0.75mm z_p2=67