一个摆线轮，其端面上的齿廓由一条短幅外摆线内侧的等距曲线与另一条曲线复合而成时，称为复合齿形。

在展成法摆线磨齿机上能够精磨的复合齿形，通常是用优化方法选出另一条满足不干涉条件的短幅外摆线的等距曲线作为顶部齿形与原摆线轮齿形不干涉部分相连而组成。要求前者既能修去原摆线轮齿因顶切而出现的尖点E（图11-10、图11-11），同时又能在最大限度保留原摆线轮不干涉部分齿形的前提下，与之较光滑地相连，如图11-13、图11-14所示。应当指出，用此法形成的复合齿形，在绝大多数情况下，这两条短幅外摆线的等距曲线只能相交，不能相切，但通过优化计算，可以使得这两条曲线交点的两条切线间的夹角比较小。

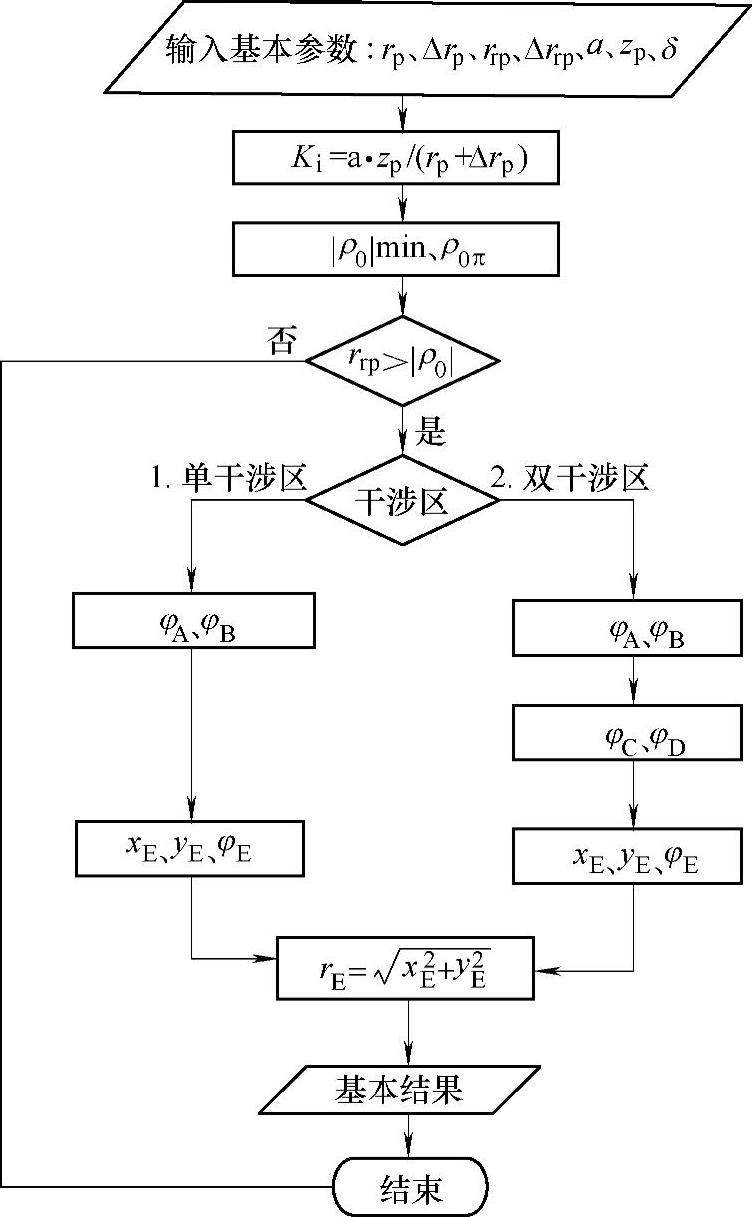
图11-12 求r_E的程序框图

这种复合齿形的设计要点如下：

1）算出有顶切的原摆线轮齿形（短幅外摆线的等距曲线）自交点E的坐标（x_E，y_E）及齿顶圆半径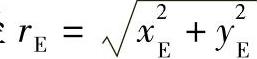（见本章2.4.1及2.4.2所述）。优选的齿顶曲线的顶圆半径r_ac2必须满足条件r_ac2＜r_E。

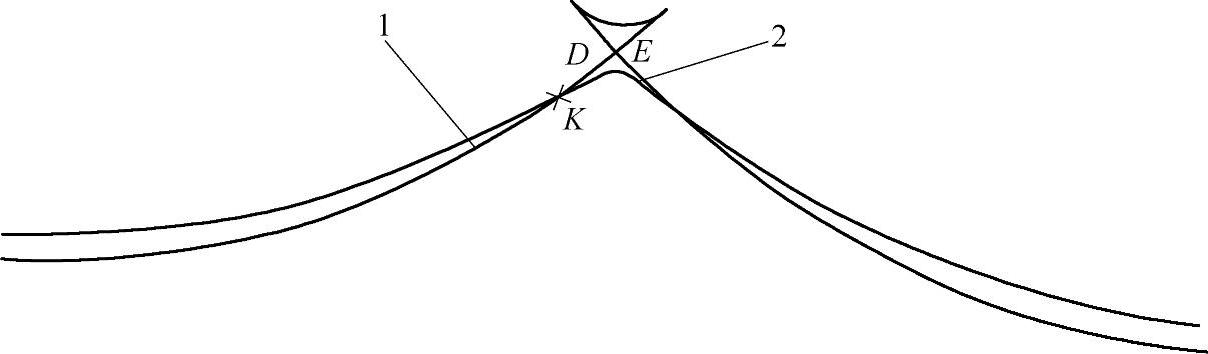
图11-13 削去单干涉区的复合齿形

1—有顶切的工作齿形L₁，其参数：r_p=131mmΔr_p=0.34mm r_rp=6mm　Δr_rp=0.46mm a=1mm r_E=125.88mm z_p=88

2—顶部齿形L₂，其参数：r_p=131.32mm r_ac=125.57mm r_rp=6.5mm　a=0.75mm　z_p=88

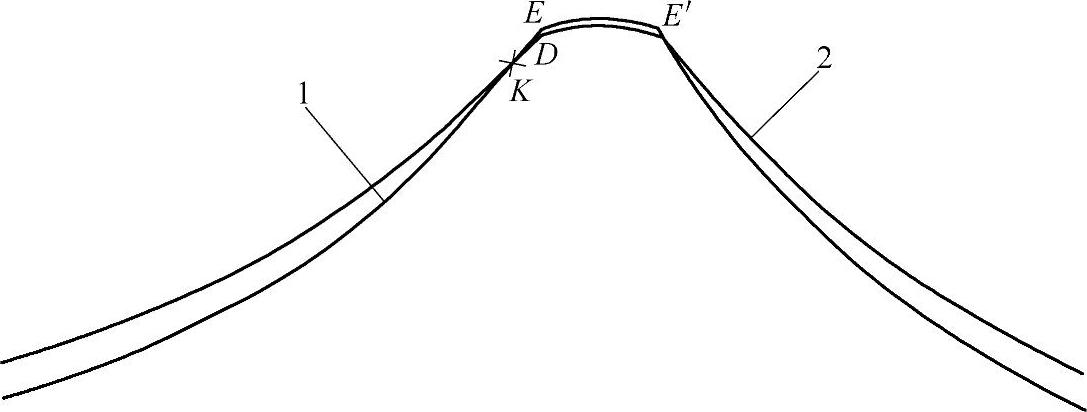
图11-14 削去双干涉区的复合齿形

1—有顶切的工作齿形L₁，其参数：r_p=275mm r_ac=267.3mm r_rp=10mm　a=2.5mm

z_c=87 z_p=88 Δr_rp=0.537mm Δr_p=0.337mm

2—顶部齿形L₂，其参数：r_p=275.9mm　r_ac=267.25mm　r_rp=10.9mm

a=2.25mm　z_c=87　z_p=88

2）算出在r_E以内，可能并需要保留的第i齿啮合点K的坐标（x_K，y_K）及K点的矢径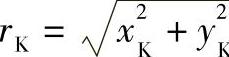，优选的齿顶曲线L₂与工作齿形曲线L₁交点D的矢径r_D应满足条件r_D＞r_K。

3）为使顶部齿形L₂与工作齿形L₁在交点处连接较光滑，很显然就要求这两条曲线在交点D的斜率差尽量小，即

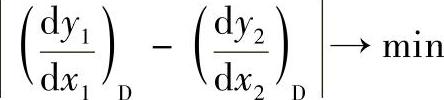
式中 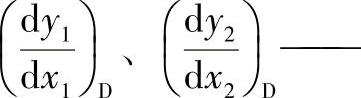曲线L₁与曲线L₂在交点D处的斜率。

为更直观，亦可用两曲线L₁与L₂在交点D处切线的夹角最小作为追求目标，要使L₁与L₂这两条曲线连接较光滑的问题就可归结为以L₁与L₂两曲线在交点D的两切线夹角为目标函数，以前面所述的几点要求（r_ac2＜r_E，r_D＞r_K及L₂曲线本身不干涉要求r_rp2-|ρ₀₂|_min＜0）作为约束条件，来求设计变量r_p2、r_rp2、a₂、z_p2（曲线L₂的诸参数）的最优化求解问题。

上述目标函数可表示为

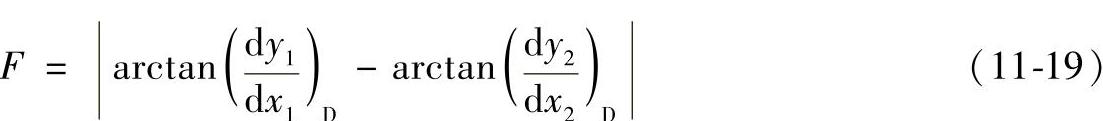
曲线L₁上任意点斜率^dy1的计算公式可利用式（11-9）将x、y分别对φ求导，首先

dx1求得：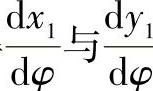

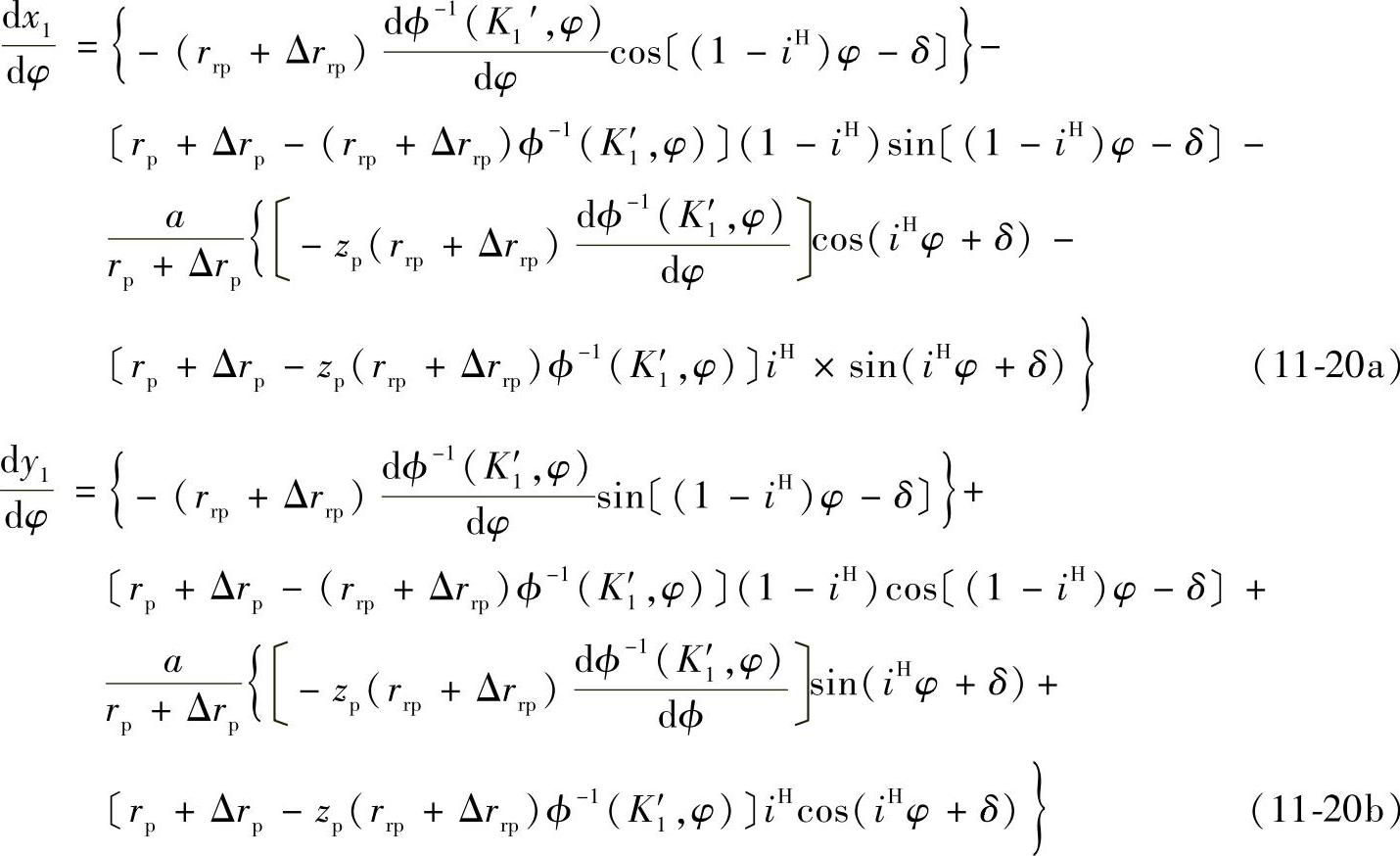
式中 r_p、r_rp、a、z_p、Δr_p、Δr_rp、δ——L₁曲线的参数；

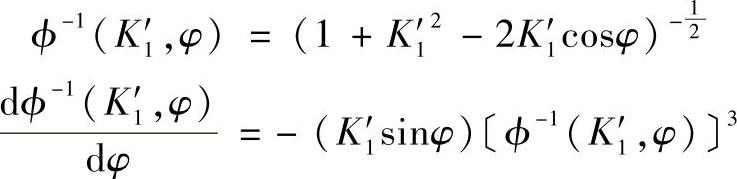
从而

将式（11-20a）、式（11-20b）代入式（11-21），即得L₁曲线上任意点斜率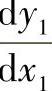的具体计算公式。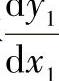

曲线L₂通常用不着移距和等距修形，故其方程式可利用式（11-9）令Δr_p=0和Δr_rp=0而获得：(www.daowen.com)

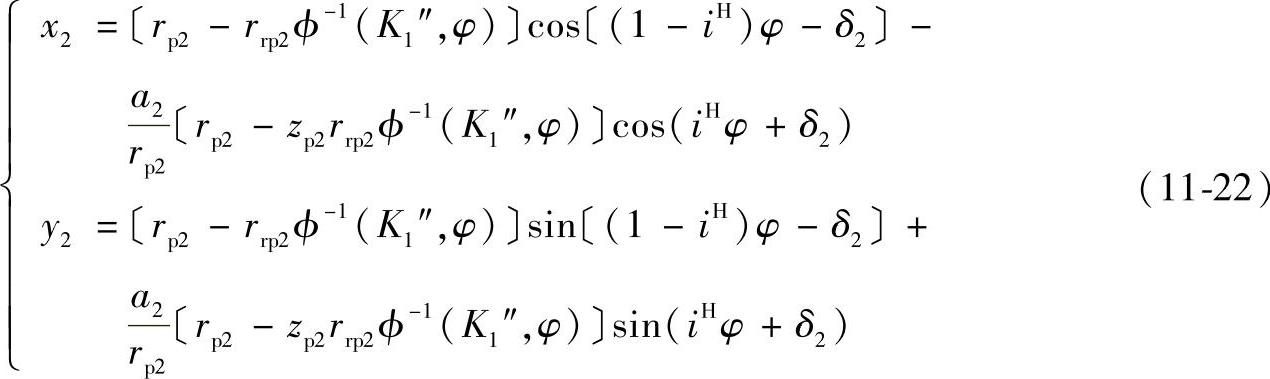
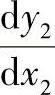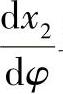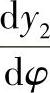其上任意点斜率的计算公式可将上式中的x、y分别对φ求导，求得与后，

再求：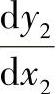

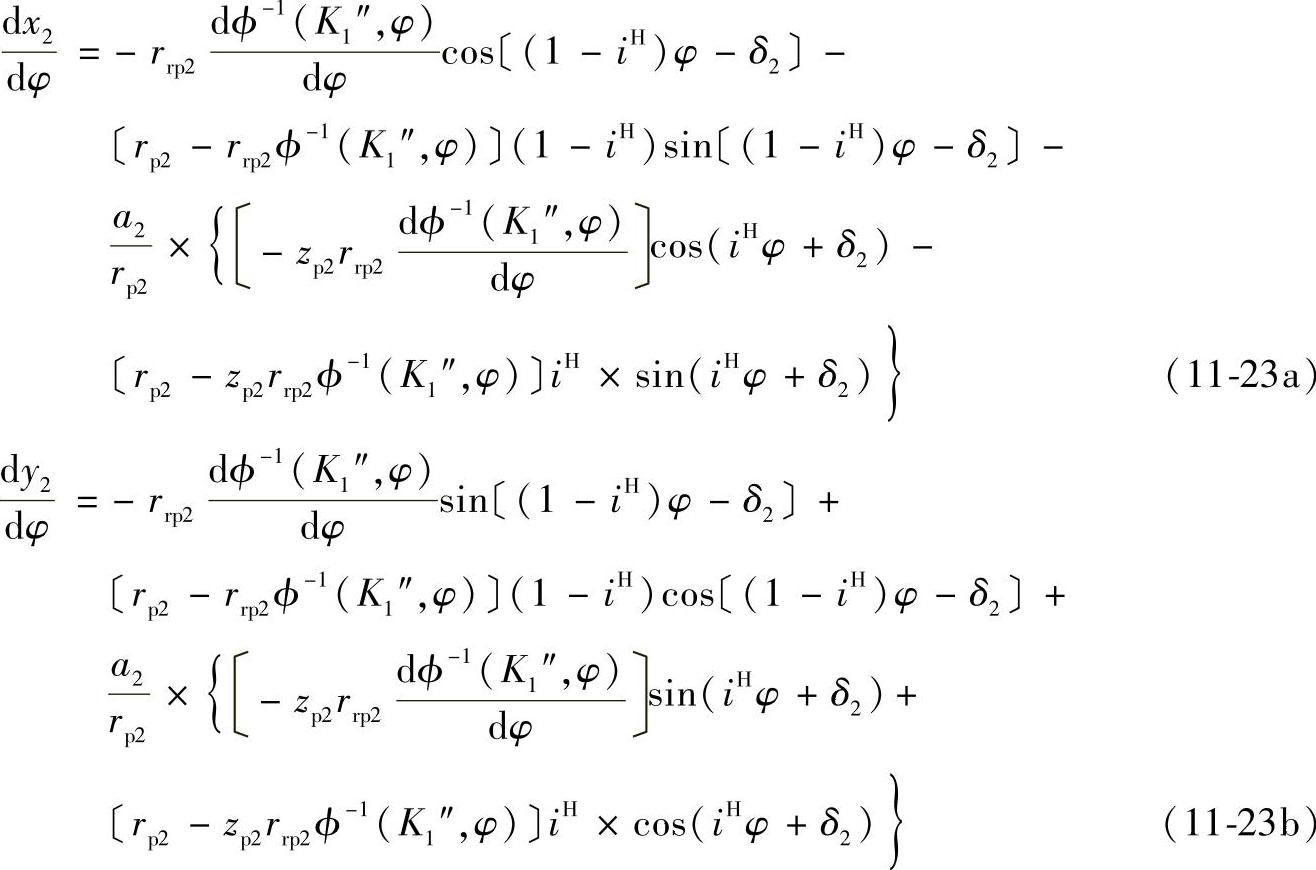
式中 r_p2、r_rp2、a2、z_p2、δ2——^L2曲线的参数；

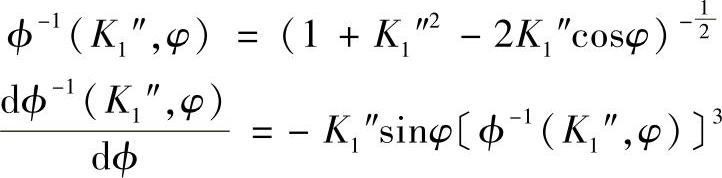
从而

将式

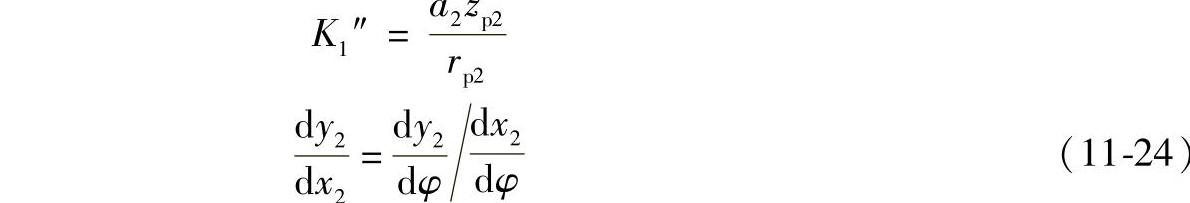
将式（11-23a）与式（11-23b）代入式（11-24）即得L₂上任意点斜率的具体计算公式。

最后，将式（11-21）和式（11-24）代入式（11-19）就可得到目标函数的具体数学模型。

4）在优选顶部齿形曲线L₂的参数r_p2、r_rp2、a₂与z_p2时，齿数z_c2=z_p2-1必须为工作齿形L₁齿数z_c=z_p-1的整数倍，即z_c2=Nz_c，N应为正整数，通常N只能取为1或2。应当注意：当N=1时，两曲线的相位角相同（图11-14），因此，式（11-22）中的δ₂=δ，而当N=2时，曲线L₂的相位角与工作齿形曲线L₁的相位角相差π/z_c2（图11-15），故此时各式中的δ₂=δ+π/z_c2。

5）顶部齿形曲线参数a₂的确定，应符合摆线磨床的标准偏心距规范，为使曲线L1与曲线L₂在交点处切线的夹角最小，通常取a₂=a/N或。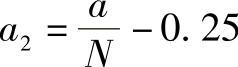

6）大传动比摆线针轮行星传动，针齿数多因结构限制装不下时，通常要隔一齿抽掉一齿，在此情况下，采用复合齿形虽可增大r_rp从而采用针齿套以提高传动效率，但往往因工作齿形的齿顶削去过多而使同时啮合齿数显著减少。因此，复合齿形设计时，一定要使同时啮合传力齿数不少于3～4齿。

7）顶部摆线L₂不得产生干涉，其齿顶圆不得大于工作摆线L₁的齿顶圆，而齿根圆不得小于工作摆线L₁的齿根圆。

8）顶部摆线L₂与工作摆线L₁在优选交点D之前不得相交，即保证不出现图11-16所示的现象，写为约束条件的形式，即

y₁（x）-y₂（x）<0{x|0<x<x_D}

式中 y₁（x）、y₂（x）——对应相同x坐标的工作摆线L₁与顶部摆线L₂的y坐标，其

值可采用数值计算方法求得。

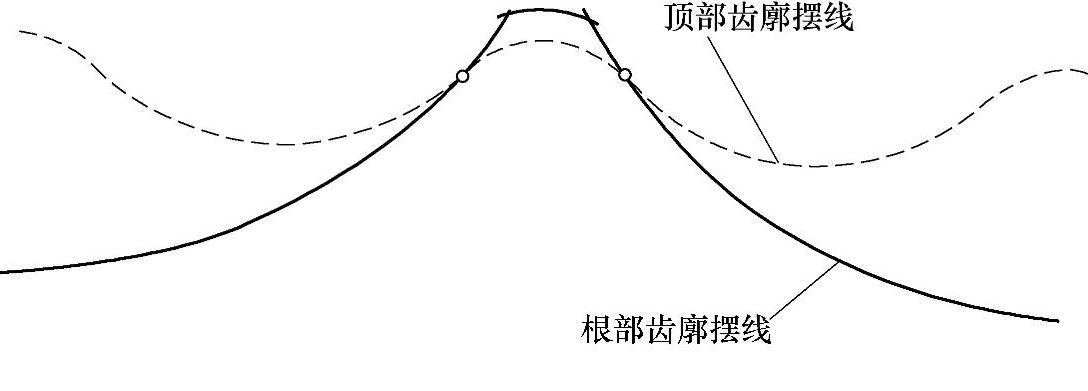
图11-15 N=2时的顶部齿形曲线

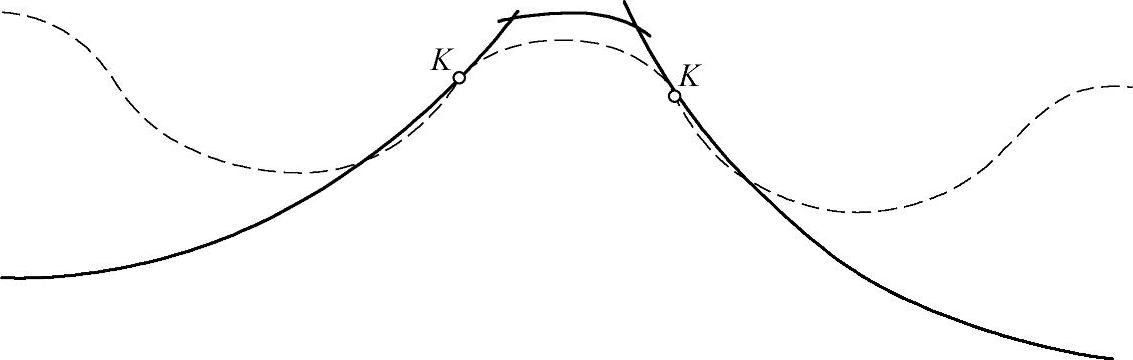
图11-16 顶部摆线与工作齿形两次相交

根据上述设计要点，设计复合齿形的实例见图11-13、图11-14。图11-13为削去单干涉区的复合齿形，有顶切的工作摆线齿形为L₁；削去前者干涉区的顶部齿形为L₂。

图11-14为削去双干涉区的复合齿形，有顶切的工作摆线齿形为L₁；优化计算得到的削去前者干涉区的顶部齿形为L₂。在这两个实例中都能保证同时有四对齿啮合传力。

复合齿形用展成法磨齿时，需先磨一次有顶切的工作齿形，再磨一次能削去干涉尖点的顶部齿形，且前后两次磨削时的偏心距不同（a₂≠a），砂轮齿形半径也不同（r_rp2≠r_rp+Δr_rp），因此磨削工艺复杂，调整、检测精度要求也较高。在某些情况下，可以只用一条完整的短幅外摆线的等距曲线来取代复合齿形，见图11-17所示，用它可以取代图11-13的复合齿形，但在此实例中只有三对齿同时啮合传力。

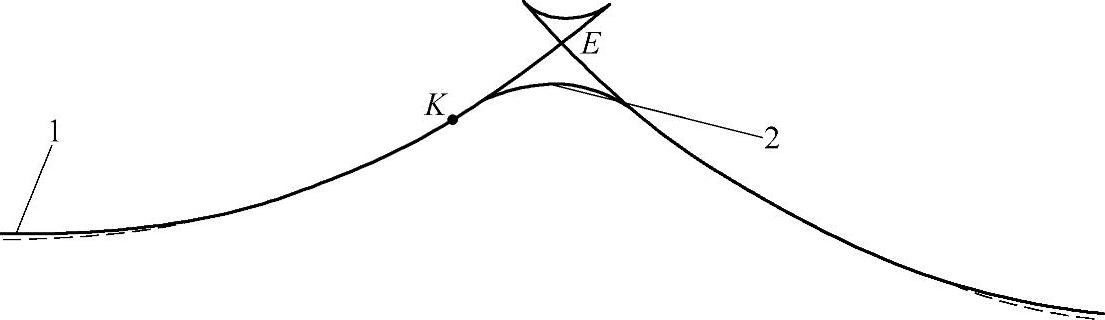
图11-17 用单一齿形取代复合齿形

1—有顶切的工作摆线齿形L₁，其参数为r_p=131mm，r_rp=6mm，a=1mm，z_p=88，Δr_p=0.34mm，Δr_rp=0.46mm，r_E=125.88mm

2—用优化方法，选取的在工作部分与L₁齿形逼近，但无顶切的新齿形L₂，其参数为r_p2=130.1mm，r_rp2=5.5mm，a₂=0.75mm，z_p2=88，r_ac2=125.35mm

在大传动比（i>43）的小型摆线针轮行星减速机中，由于采用复合齿形的磨削工艺复杂，为了降低制造成本，也可改用不带针齿套的微变幅（K₁≈1）摆线针轮行星传动以提高传动效率。