设计复合齿形必须知道原齿廓顶切后的齿顶圆半径，现讨论其求法：

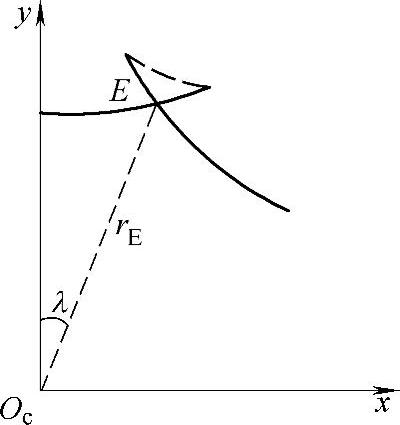
1）当r_rp≥|ρ₀π|时见图11-10，此时顶切后干涉区形成的尖点E即摆线轮的齿顶，r_E即为齿顶圆半径，其求法如下：

由对称关系可知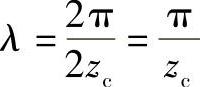

设E点坐标为（x_E，y_E）

则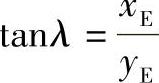

由通用的摆线轮齿形方程式，并考虑到图11-10坐标轴的取法与图11-6的区别，可得

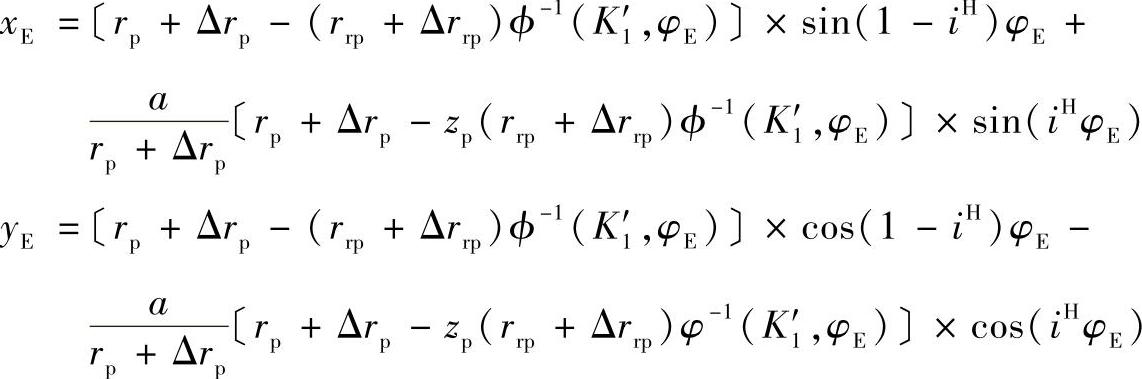
式中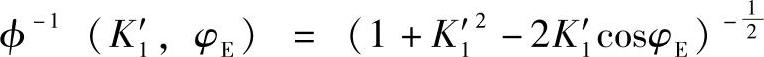

其余符号同前

已知r_p、Δr_p、r_rp、Δr_rp、z_p、i^H、a、K′₁=az_p/（r_p+Δr_p），通过上面各式联立，在计算机上求解，可求得x_E、y_E及φ_E，然后根据图11-10可求得。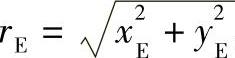

(www.daowen.com)

图11-10 单干涉区

2）当|ρ₀|_min＜r_rp＜|ρ₀π|时见图11-11，此时在一齿范围内有两处干涉区，形成两个尖点（短幅外摆线的等距曲线的自交点）E与E′。为把干涉区修掉，暂取E点处的矢径长r_E为摆线轮的齿顶圆半径，即把r_E以外的部分修整掉。

摆线轮齿顶圆半径为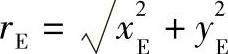

下面介绍一种用微机计算求x_E与y_E的方法：

见图11-11，首先求出干涉界限点A和B的坐标和啮合相位角φ_A、φ_B，然后在φ=φ_B～180°之间找出与A点同一x坐标下的点C及其啮合相位角φ_C，同理在φ=0～φ_A之间求出与B点同一x坐标下的点D及其啮合相位角φ_D。最后，在φ=φ_D～φ_A和φ=φ_B～φ_C二个区间内找出具有同一x、y坐标值的点，此点的坐标值就是交点E的坐标值x_E、yE。求rE的程序框图见图11-12。

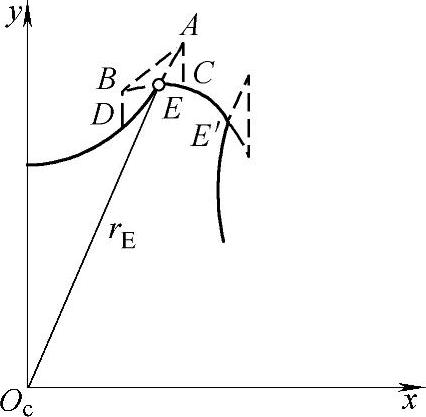
图11-11 双干涉区

例11 - 1 已知r_p=165mm，r_rp=6mm，a=1.5mm，z_p=88，Δr_rp=0.44mm，Δr_p=0.29mm，δ=0，求r_E。

解 求r_E的程序框图见图11-12。用计算机求得本例属双干涉区，E点的矢径长r_E=160.28mm。