摆线轮齿廓的内凹部分不会产生干涉，只需研究理论齿廓外凸部分的干涉情况。常见的情况有两种：

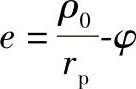1）当短幅系数K₁满足不等式时摆线针轮减速机常用K₁大多属此范围。参看表11-1中第Ⅰ类参数范围的曲线的特征，可以看出，干涉有两种形式：

①当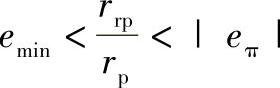时，即|ρ₀|_min<r_rp＜|ρ₀π|时，在啮合相位角φ=0°～180°范围内，干涉区有起、止点，见图11-9。即从某一φ₂开始产生干涉现象，到另一φ₃值干涉现象消失。因而在φ=0°～360°之间，即一个完整摆线轮齿范围有两处干涉区，此时齿形干涉的情况如图11-11所示。

②当eπ|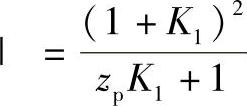时，即r_rp≥|ρ₀π|时，见图11-9，干涉区从某一φ₁开始直到180°始终存在，因而在φ=0°～360°之间，即一个完整摆线轮齿范围只有一处干涉区。此时齿形干涉的情况如图11_-10所示。

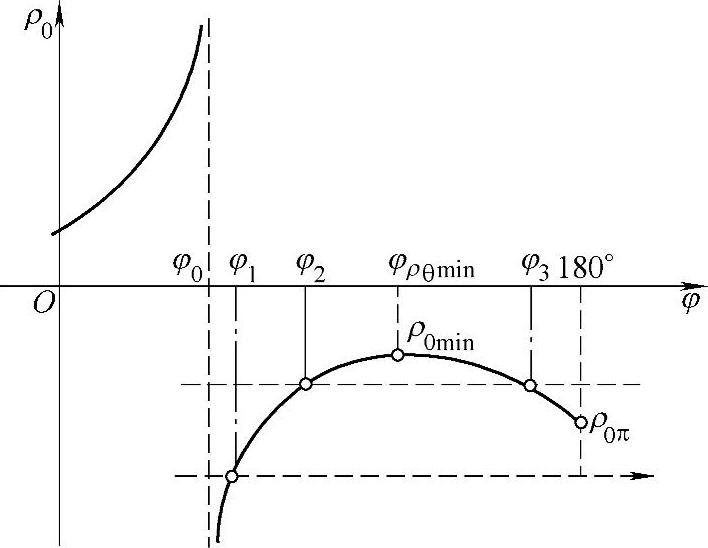
图11-9 摆线轮理论齿廓（短幅外摆线）的曲率半径

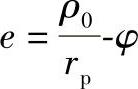2）当短幅系数K₁满足不等式时 参看表11-1中第Ⅱ类参数范围的曲线的特征，可以看出，若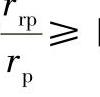eπ|时，亦即r_rp≥|ρ₀π|时，则干涉区从某一φ开始直到180°始终存在，因此在一个完整的摆线轮齿范围内只有一处干涉区。(www.daowen.com)

齿形干涉区的界限点（起止点）所对应的啮合相位角可按下式求出：

令ρ₀=-r_rp（理论齿形外凸处ρ₀为负）

即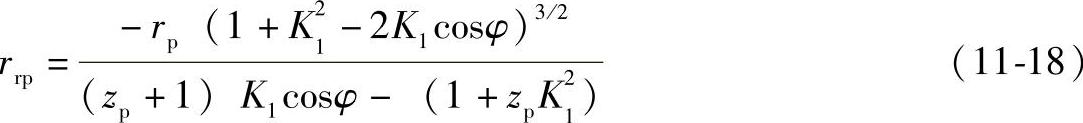

从式（11-18）解出之φ即为干涉区界限点所对应的啮合相位角。

式（11-18）可以化成三次代数方程求解，也可以应用微分几何中求曲线奇异点的方法求解，用计算机解超越方程的办法来解更为方便。

利用计算机解式（11-18），首先要判断干涉的类型。如为单干涉区，则在φ=0°～180°之间得到一解即为起始干涉点，干涉终点为起始点的对称点。如果是双干涉区，则需在φ=0°～φ和φ～180°之间各求得一解，分别为干涉区的起点和终点，一个摆线轮齿的另一侧干涉区为前一干涉区的对称位置。

当求得干涉区界限点所对应的啮合相位角φ，即可代入式（11-9）求得界限点的坐标。