摆线轮理论齿廓曲线的曲率半径ρ₀，根据微积分的公式可求得

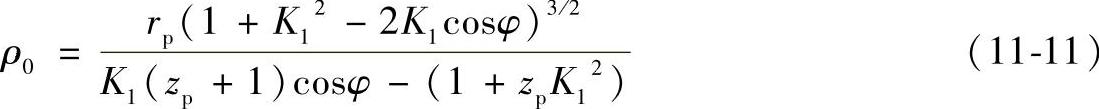
ρ₀值为正，曲线向内凹，ρ₀为负值，曲线外凸（图11-8a）。

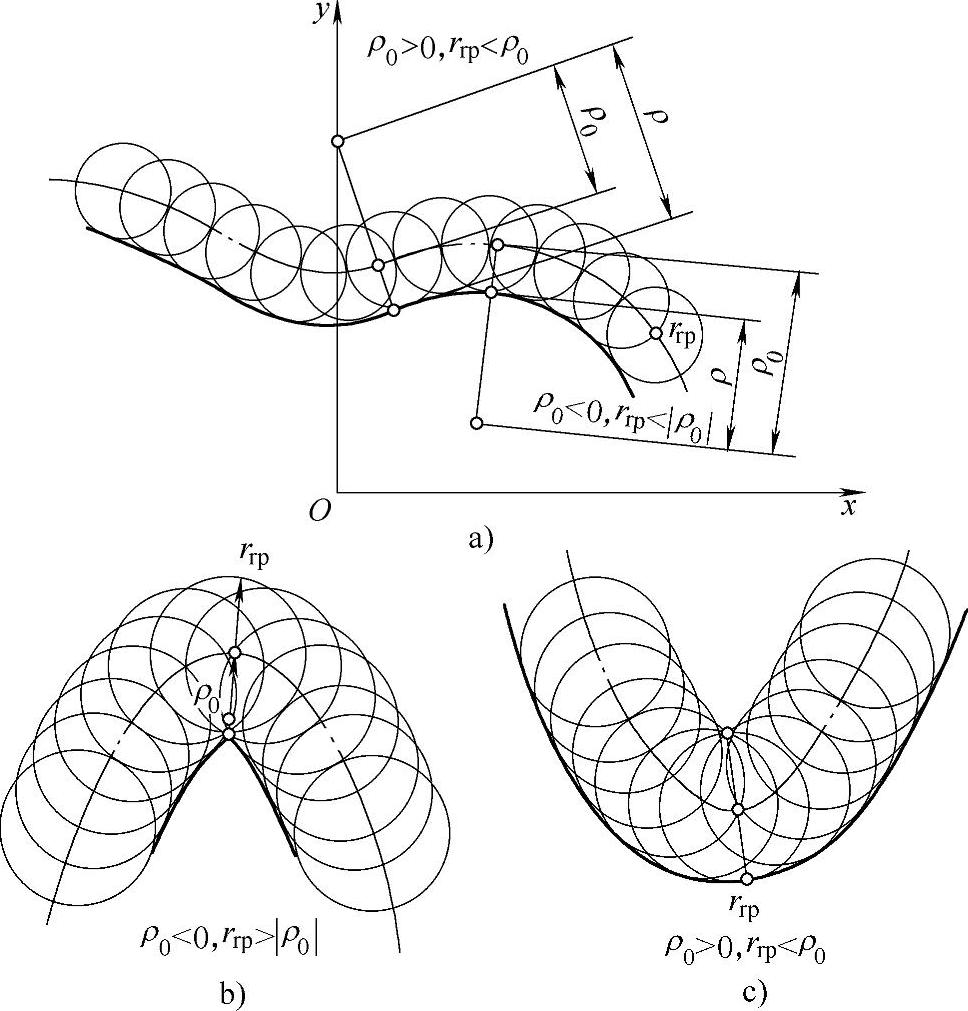
图11-8 摆线轮的实际齿廓和顶切

摆线轮实际齿廓曲线的曲率半径（图11-8）为

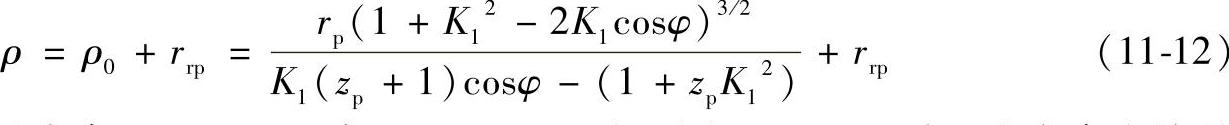
对于外凸的理论齿廓（ρ₀＜0），当r_rp>|ρ₀|时（图11-8b），则理论齿廓在该处的等距曲线就不能实现，即等距曲线成交叉齿廓，以致在加工时切除了部分有效的齿廓曲线，这种情况称为“切齿干涉”，会破坏连续平稳的啮合，当然是不允许的。当r_rp=|ρ₀|时，ρ=0，即摆线轮齿廓在该处出现尖角。也应防止。若ρ₀为正值（图11-8c），不论r_rp取多大，摆线轮实际齿廓都不会发生类似现象。

摆线轮齿廓是否发生顶切，不仅取决于理论外凸齿廓的最小曲率半径|ρ₀|_min，而且与针齿齿形半径（带针齿套时即针齿套半径）有关。根据理论推导，最小曲率半径|ρ₀|_min的计算公式列于表11-1。

表11 - 1 最小曲率半径|ρ₀|_min的计算公式(www.daowen.com)

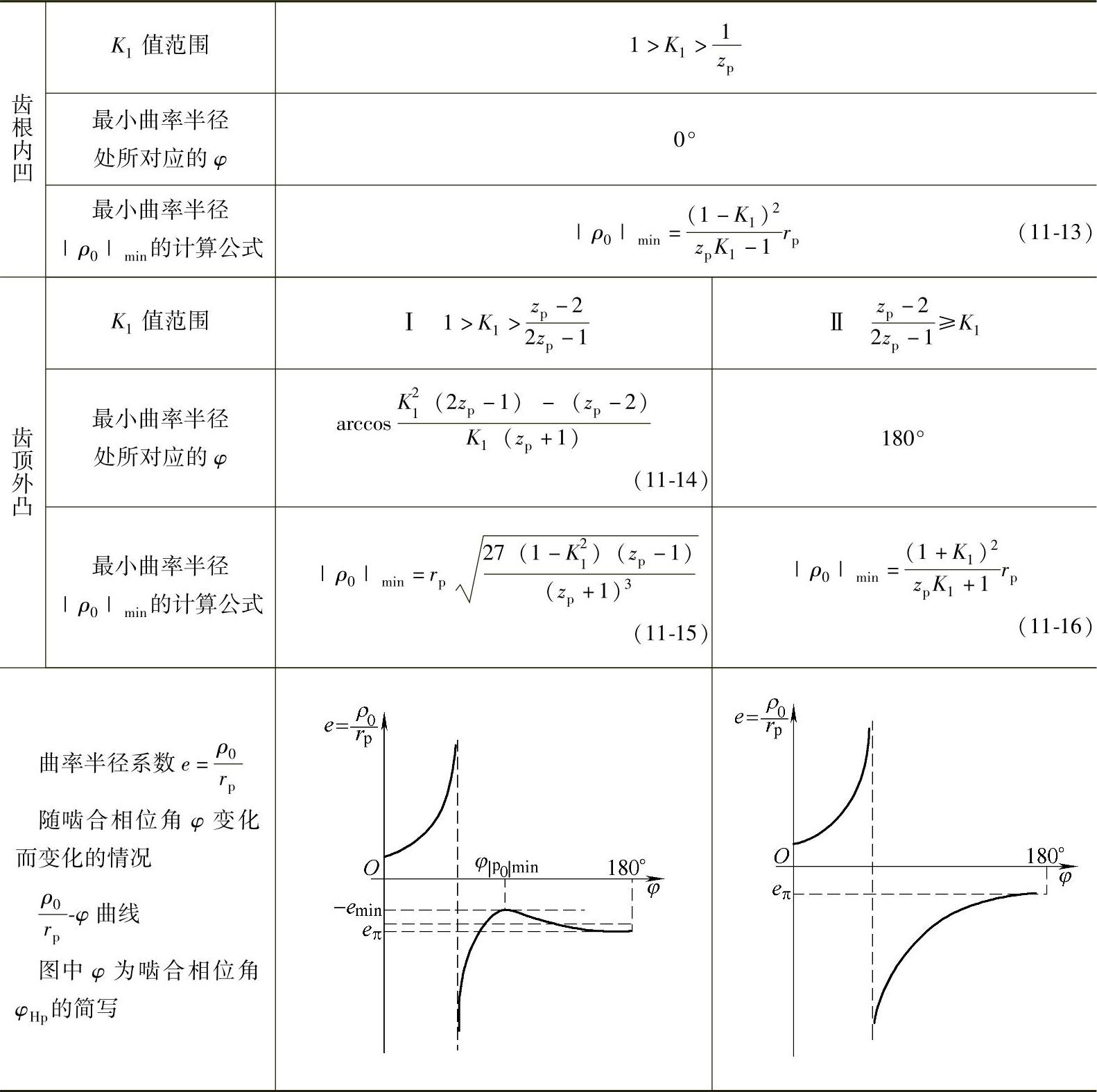
表中同时

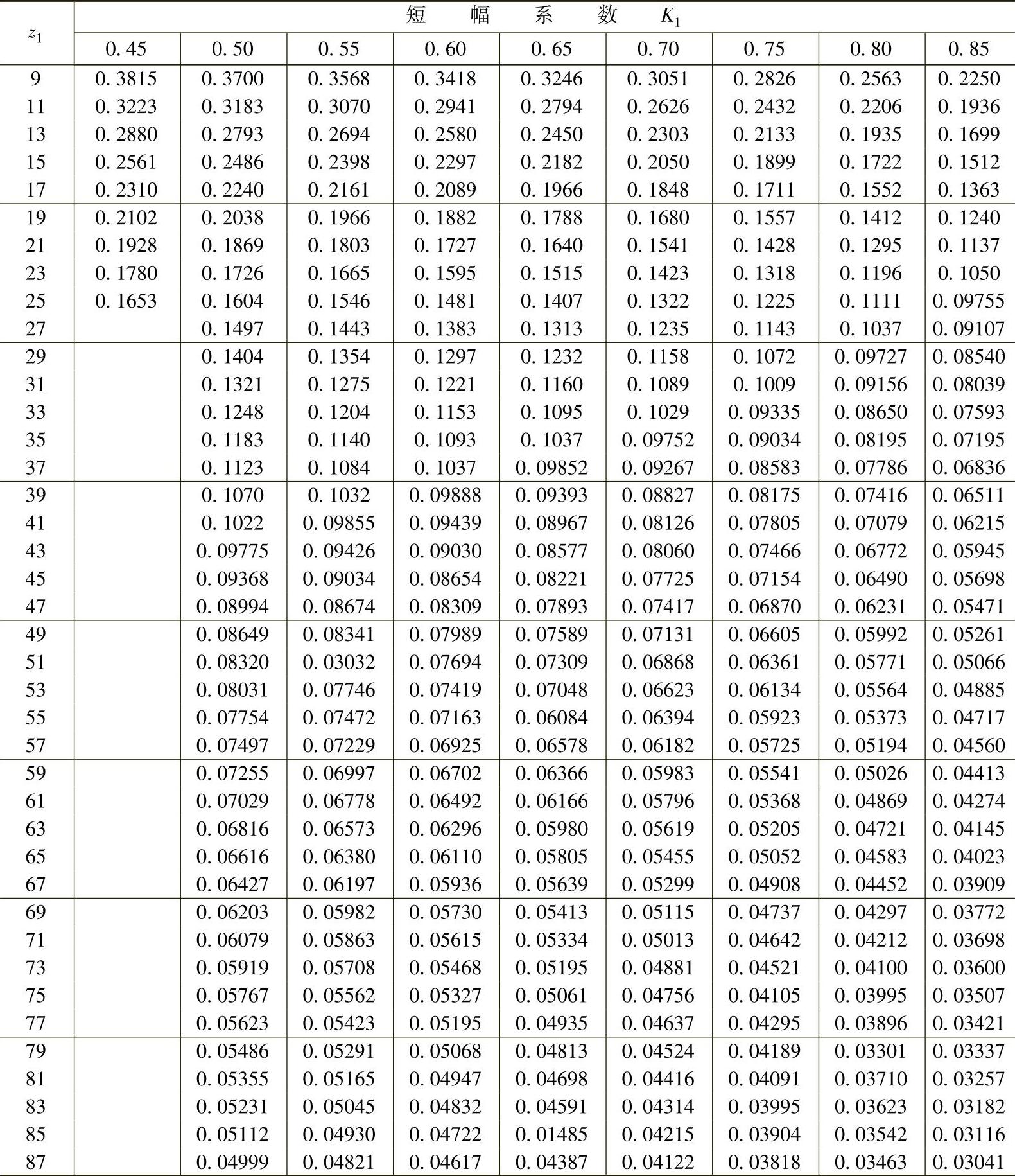
给出|ρ₀|_min处所对应的啮合相位角φ|ρ₀|_min。按表中公式可以算出比值ρ₀|_min/r_p=e_min，称为最小曲率半径系数，列于表11-2。

按表11-2查出e_min即可算出|ρ₀|_min=e_minr_p。

摆线轮齿廓不产生顶切或尖角的条件可表示为

或

表11 - 2 摆线轮理论齿廓的最小曲率半径系数emin