见图11-3当半径为r_g的滚圆（发生圆）在固定的半径为r_bc的基圆上纯滚动时，滚圆周上一点B的轨迹B₁B′B″B‴B₂称外摆线，而滚圆内一点M的轨迹M₁M′M″M‴M₂称短幅外摆线（属变幅外摆线）。比值O′M/r_g=K₁称短幅系数。

以外摆线、短幅外摆线上连续的无数点为圆心，以r_rp为半径画出无数圆，这一系列圆的内、外包络线称这二曲线的等距曲线（图上只画出内侧的等距曲线）。

若O′M>r_g，此时K₁>1，则M点的轨迹为长幅外摆线。

摆线针轮行星传动中摆线轮的齿廓大多采用短幅外摆线的内侧等距曲线，但在特定情况，也可用长幅外摆线的等距曲线。

除上述滚圆在基圆外侧作外切的纯滚动形成外摆线、变幅外摆线及其等距曲线的方法外，还有第二种形成方法，见图11-4。半径为r′_p的滚圆套在半径为r′_c的基圆上，二者中心距a=r_p′-r′_c，当滚圆沿基圆的外侧作内切的纯滚动时，滚圆上一点B的轨迹BB′B″B‴B₁为外摆线；在滚圆外与滚圆相固连的一点M的轨迹MM′M″M‴M₁为短幅外摆线。

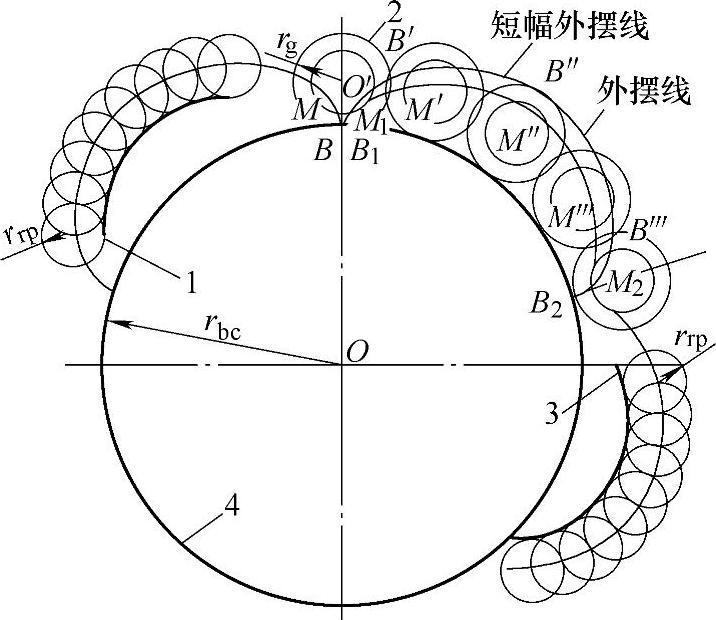
图11-3 短幅外摆线形成原理

1—外摆线的等距曲线 2—滚圆 3—短幅外摆线的等距曲线 4—基圆

内啮合的摆线针轮传动就是以短幅外摆线MM′M″M‴M₁作为摆线轮的理论齿廓，而M点就是针轮针齿的理论齿廓。实际上，传力的针齿是以M为中心，以r_rp为半径所画的圆作为齿廓，而用短幅外摆线的内侧等距曲线（即以短幅外摆线MM′M″M‴M₁上连续的一系列点为圆心，以r_rp为半径画出的一系列圆的内包络线）作为摆线轮的实际齿廓。用这种方法形成的针轮齿廓与摆线轮齿廓必然互为共轭曲线。用来传动，基圆r′_c就是摆线轮的节圆，而滚圆r_p′是针轮的节圆，摆线轮与针轮的啮合传动相当于这两个节圆作纯滚动，当然必满足传动比i等于常数的基本要求。两节圆的接触点P称为节点。针齿与摆线轮齿廓接触的公法线通过节点P。

从图11-4看出，当滚圆r′_p绕基圆r′_c顺时针方向作纯滚动时，每滚过滚圆的圆周长2πr′_p时，滚圆上的一点B在基圆上就形成一整条外摆线BB′B″B‴B₁。滚圆的圆周长2πr′_p比基圆的圆周长2πr′_c长2πr′_p-2πr′_c=2π（r_p′-r′_c）=2πa，当r′_p圆上的B点在滚圆滚过圆周长2πr′_p再次与r′_c圆接触时，应是在r′_c圆上的B₁点，而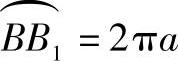，这也就是摆线轮基圆r′_c（在传动中，此基圆即摆线轮的节圆）上的一个齿距p，即

p=2π（r′_p-r′_c）=2πa （11-1）

由此可得摆线轮的齿数

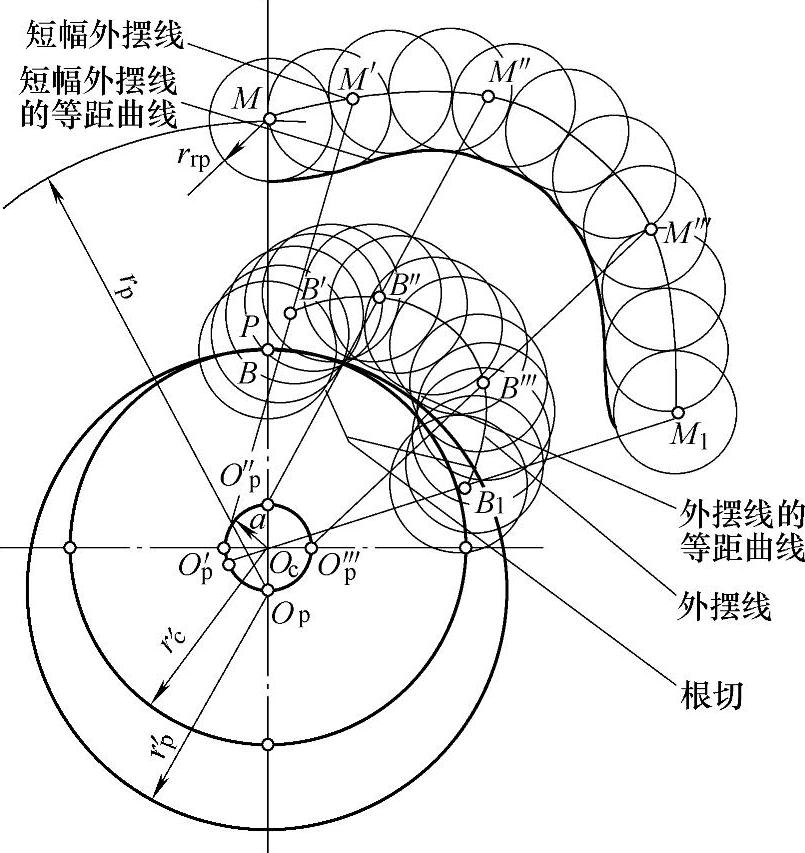
图11-4 形成外摆线与短幅外摆线的第二种方法

针轮齿数

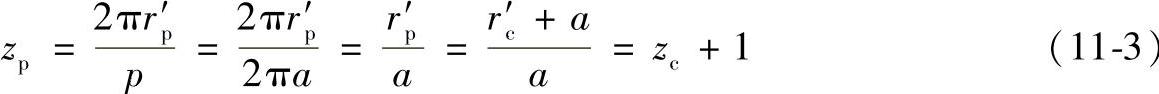(www.daowen.com)

无论用外摆线还是用短幅外摆线的等距曲线做齿廓，一整条循环曲线所对应的基圆上的弧长都是同一个周节p，故式（11-1）～式（11-3）对二者都适用。

把一整条的短幅外摆线的等距曲线都用作摆线轮的齿廓，使摆线轮的全部齿廓是由z_c支整条的循环曲线组成的连续曲线，要求基圆半径r′_c与滚圆半径r_p′之比，即摆线轮的节圆半径与针轮节圆半径之比，满足下面的条件：

图11-4所示，与短幅外摆线等距曲线为齿廓的摆线轮相啮合的针轮，它的针齿中心圆半径为r_p。针轮的节圆半径r_p′与r_p的比值，即短幅系数K₁为

当K₁=1时，即r_p=r′_p外摆线的等距曲线与针齿相啮合；当K₁<1时，短幅外摆线的等距曲线与针齿相啮合。

在r_p圆上，针齿间的齿距

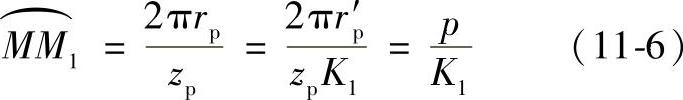
形成短幅外摆线及其等距曲线的两种方法，实际上就是用展成法切削与精磨摆线轮齿廓的理论基础。用沿基圆的外侧作外切或内切的纯滚动法形成同一短幅外摆线的条件（图11-5）是：

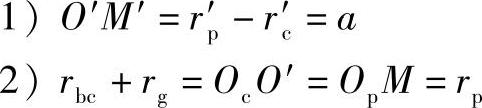
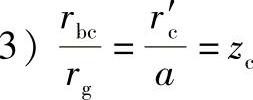
用以上三式联立，有下述关系：

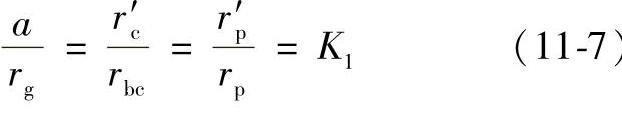
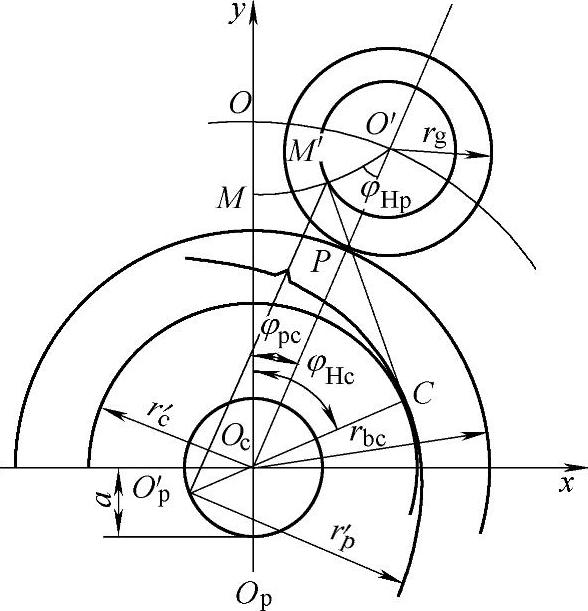
图11-5 两种方法等效形成同一短幅外摆线的原理