
(1)确定变位系数的试算法
试算法是一种较为常用的选取变位系数的方法,其计算公式也是其他各种计算方法的基础。
试算法首先选取一个合适的啮合角α′,然后假定一个外齿轮变位系数x1,根据齿轮无齿侧间隙啮合方程求取y02或x2,再按齿廓不重叠干涉与重合度大于1两个条件进行校核。若不满足要求,则再选定一个x1,重复上述计算,直至满足为止。
以外齿轮滚齿,内齿轮插齿为例,计算步骤如下:
1)根据齿数差,选取内齿轮副的啮合角α′
Δz=z2-z1=1;α′=54°~56°
Δz=z2-z1=2;α′=37°~40°
Δz=z2-z1=3;α′=28°~30°
Δz=z2-z1=4;α′=25°~27°
2)假定一个x1(在重复计算中,x1可假定为0.5,1,1.5,2,…),代入下式求出外齿轮的齿厚增量:
Δ1=2x1tanα (10-1)
当用插齿刀插制外齿轮时
式中
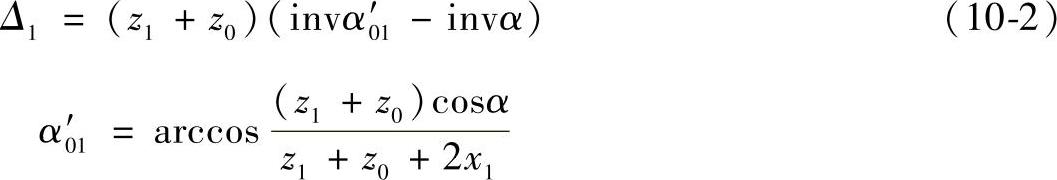
3)将Δ1代入无齿侧间隙啮合方程,求出内齿轮的齿厚增量(负值)
Δ2=(z2-z1)(invα-invα′)-Δ1 (10-3)
4)将Δ2代入下式求出插制内齿轮时的制造啮合角α0′2:

5)将α0′2代入下式求出插制内齿轮时的中心距变动系数:

当内齿轮用假想齿条刀具切制时,则变位系数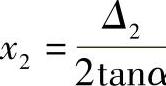 ,x2与y02的关系式如下:
,x2与y02的关系式如下:
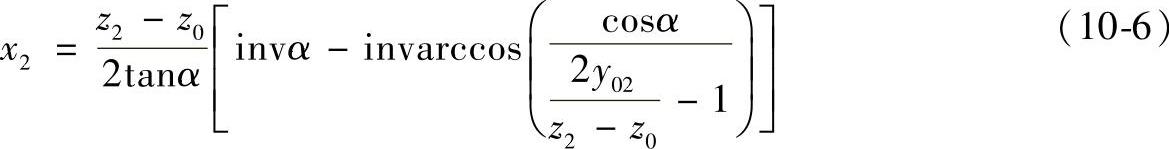
6)进行Gs>0与ε>1的校核
①Gs>0的校核
Gs=z1(invαa1+δ1)-z2(invαa2+δ)+(z2-z1)invα′>0 (10-7)
式中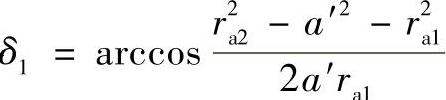 ;
;
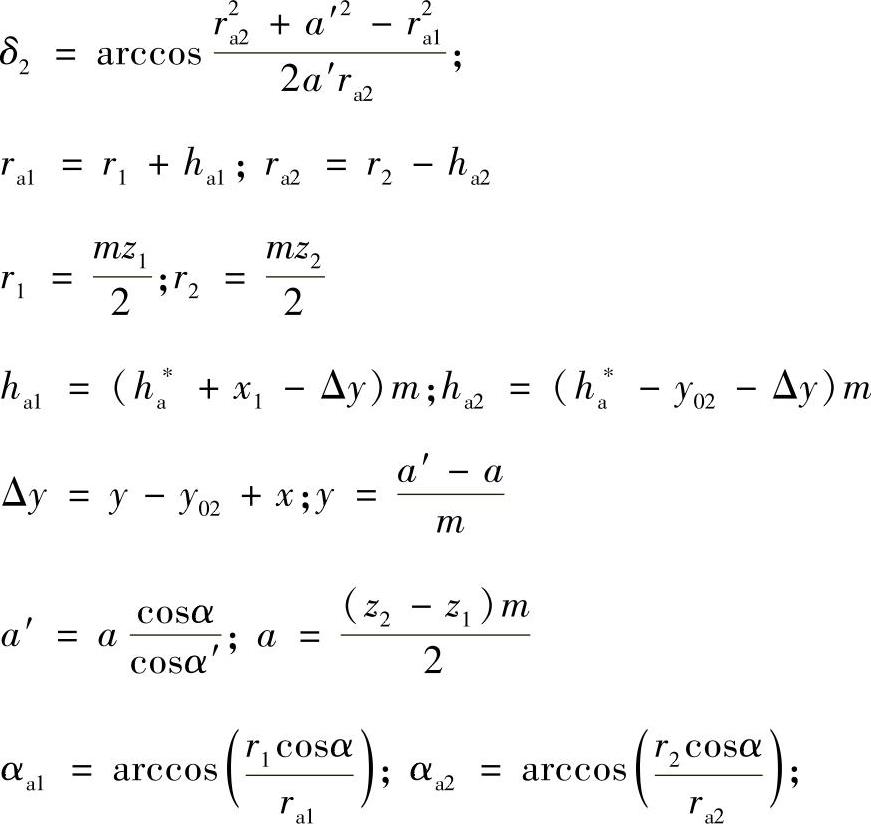
αa1、αa2分别为外齿轮与内齿轮的齿顶压力角。
②ε>1的校核
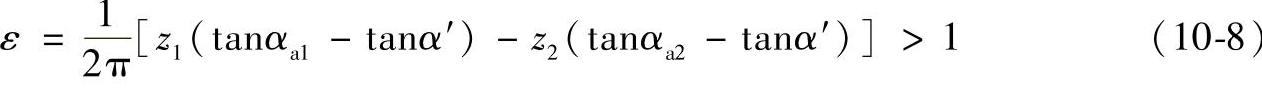
此法如无经验,往往要反复计算数次才能成功,计算工作量较大。有时即使找到了符合限制条件的x1与y02(或x2),也不一定是较佳的参数,盲目性较大。
(2)作封闭图法
作封闭图选择变位系数,它的优越性在于可揭示主要限制条件与各几何参数的关系。封闭图由数条等啮合角曲线与三条限制曲线组成。计算时假定外齿轮为滚齿,内齿轮为插齿,α=20°,ha*=0.8,c*=0.3,其计算方程式为:
1)等啮合角曲线方程
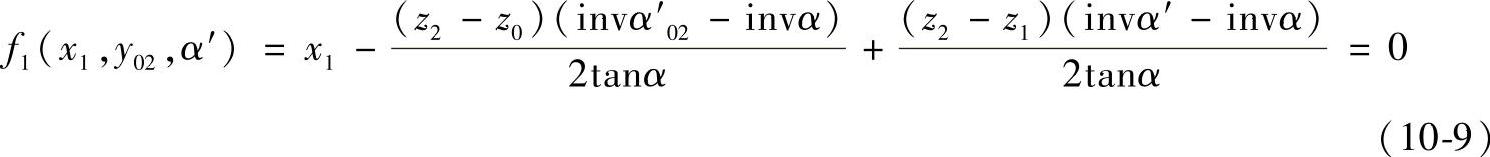
2)齿廓不重叠干涉Gs=0的限制曲线方程
f2(x1,y02,α′)=z1(invαa1+δ1)-z2(invαa2+δ2)+(z2-z1)invα′=0 (10-10)
3)重合度ε=1的限制曲线方程
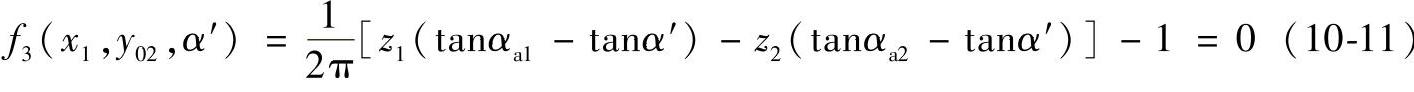
4)齿顶高变动系数Δy=0的曲线方程
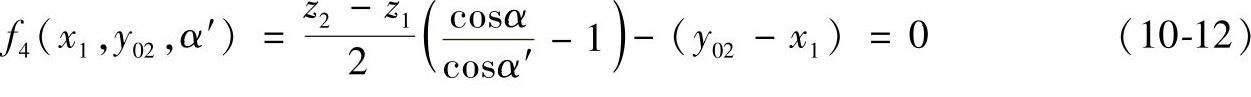
根据上述方程,可计算出一系列的封闭图。由于篇幅有限仅选择图10-21~图10-24为一齿差的四例;图10-25~图10-28为二齿差的四例,在图10-21中所示的曲线1为不同的等啮合角曲线,曲线2为重合度ε=1的曲线,曲线3为Gs=0的曲线,曲线4为齿顶高变动系数Δy=0的曲线。
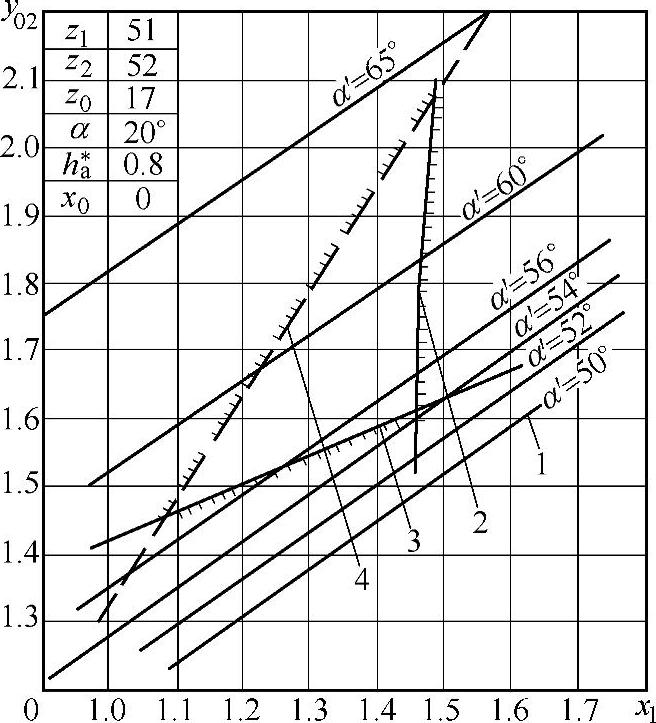
图10-21 一齿差z0=17封闭图
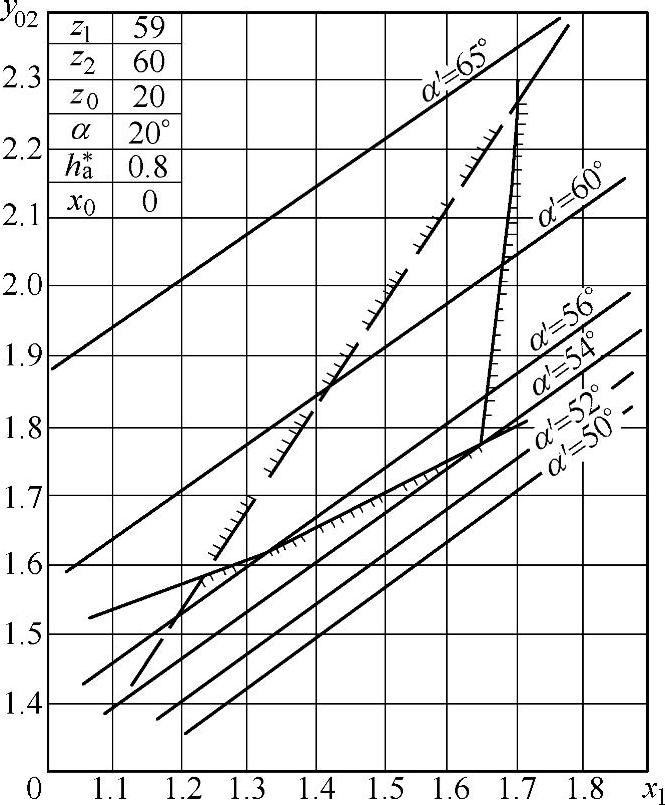
图10-22 一齿差z0=20封闭图
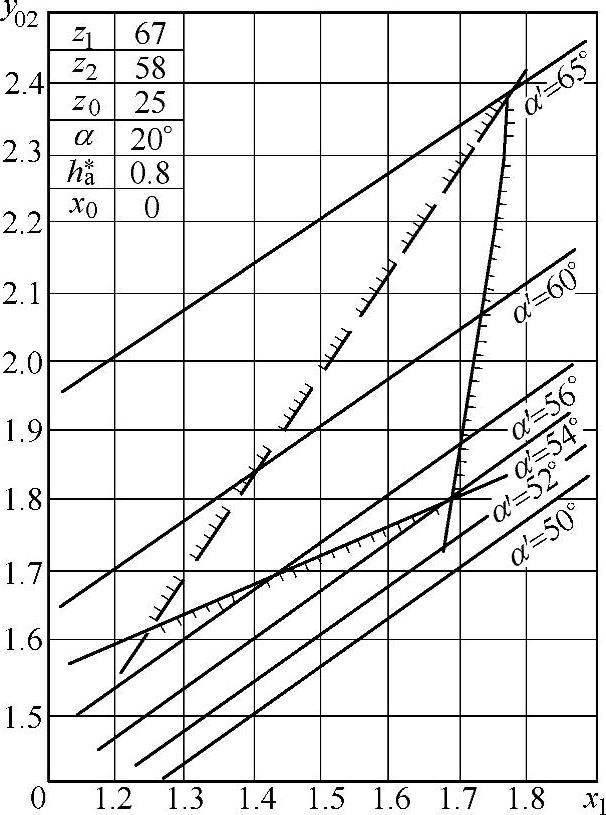
图10-23 一齿差z0=25封闭图
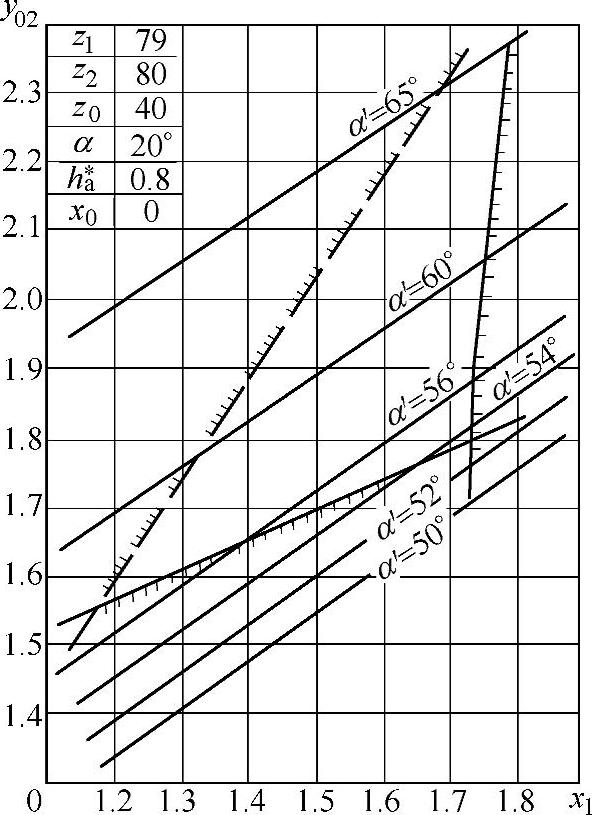
图10-24 一齿差z0=40封闭图
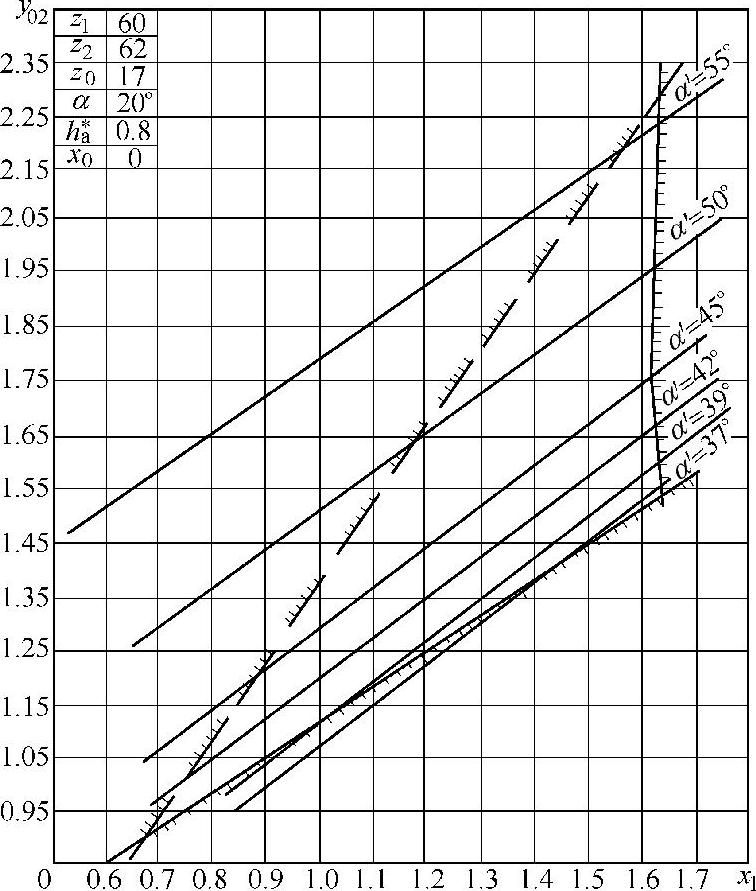
图10-25 二齿差z0=17封闭图
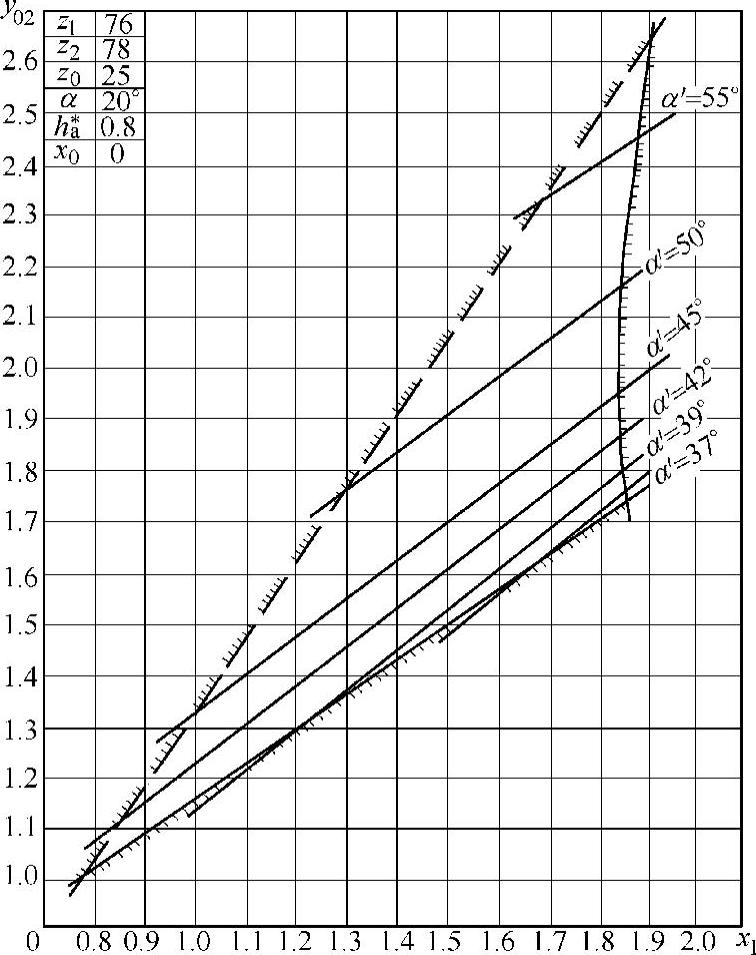
图10-26 二齿差z0=25封闭图
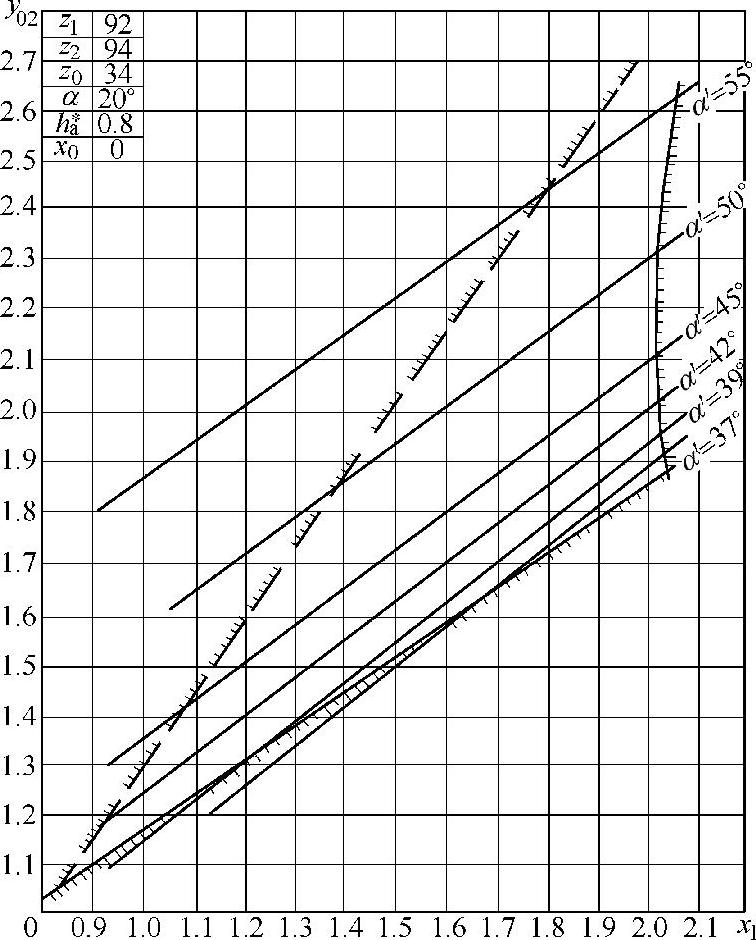
图10-27 二齿差z0=34封闭图
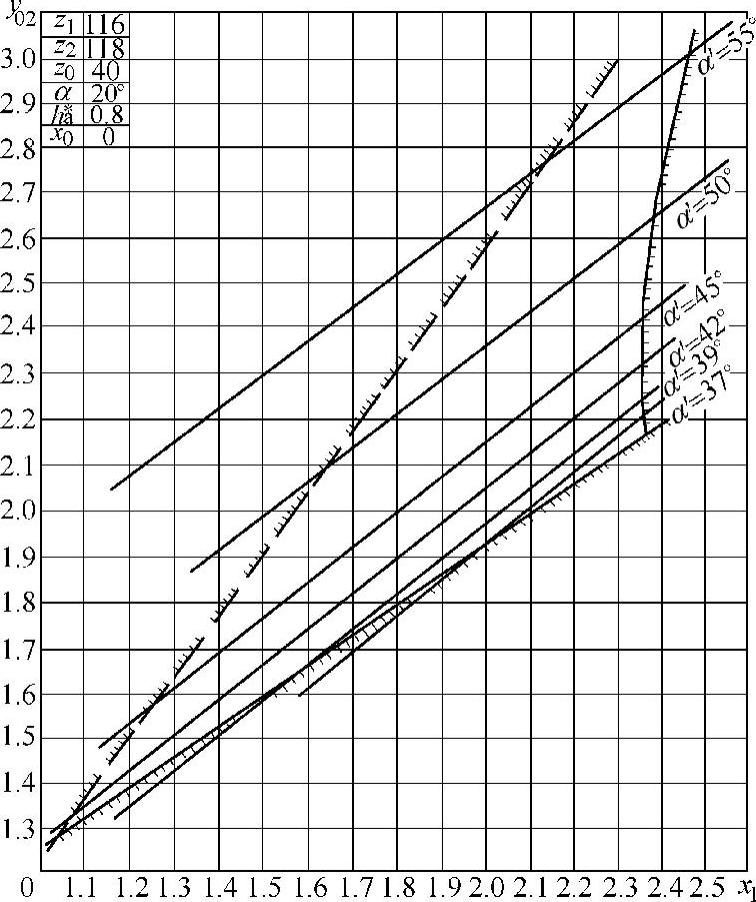
图10-28 二齿差z0=40封闭图
从封闭图可知,在由Gs=0,ε=1,Δy=0三条曲线围成的区域中选取的x1与y02总是符合不干涉要求的,一般在较小的等啮合角线上选择,并取靠近Gs=0曲线附近的点,它有两个好处:一是重合度较大,传动平稳;二是变位系数较小,可改善齿顶变尖,降低齿廓的滑动系数。这种方法只能在有封闭图资料的情况下才可取,而非封闭图的工作量是较大的。(www.daowen.com)
(3)查几何参数表法
随着计算机的普及,借助计算机的辅助设计与分析,将变位系数的选取和齿轮副其他参数一起用计算机完成,列成表格,直接供查表选用是十分方便的。计算原则在选取变位系数时,既要满足Gs>0,但也不宜过大,事先给定一个很小的值,Gs=0.05,然后解出变位系数与齿轮其他参数,显然这样做使重合度提高,变位系数降低,较为合理。
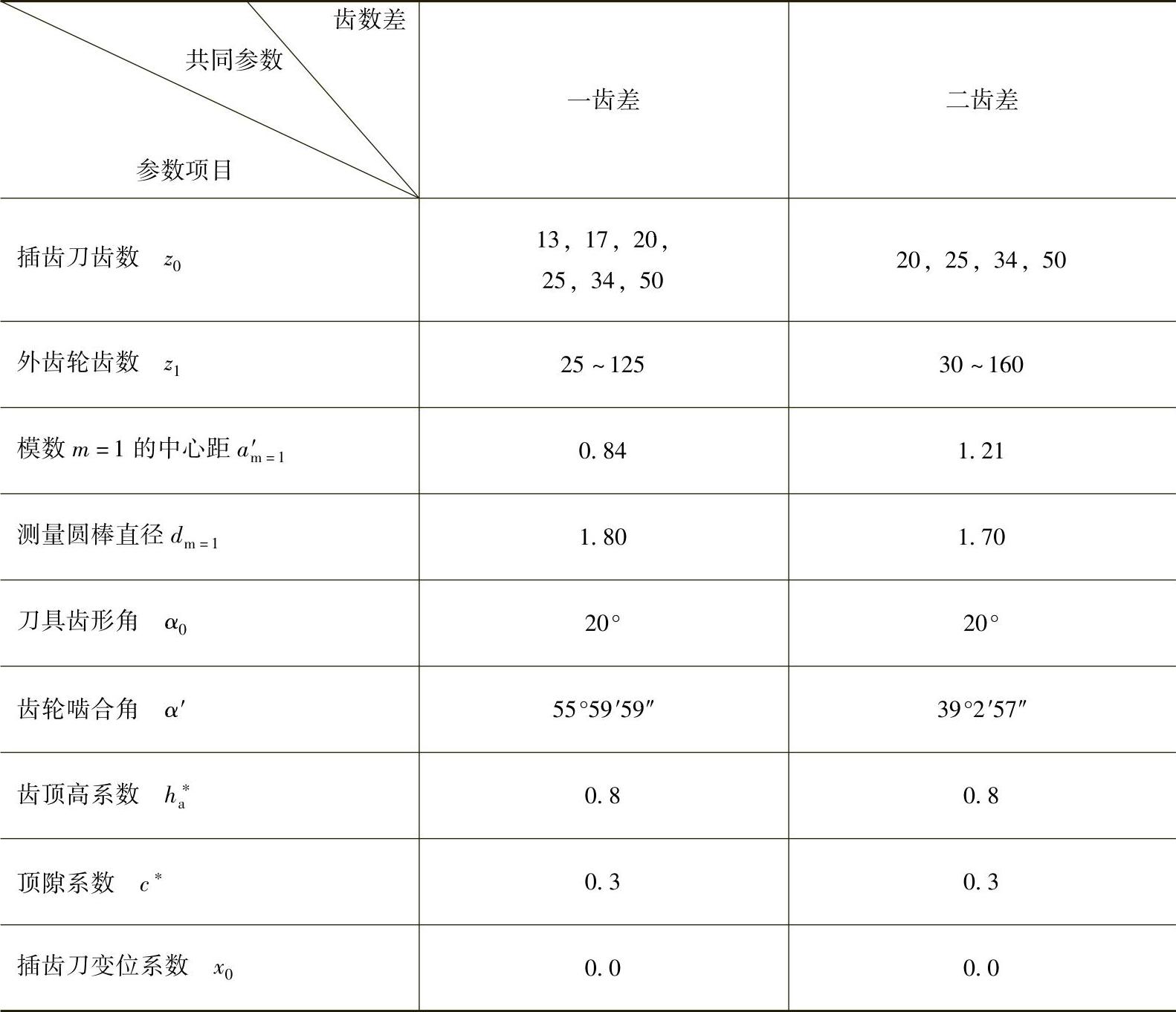
几何参数表的计算其共同参数见表10-5。
表10 - 5 几何参数表的计算共同参数
一齿差几何参数表见表10-6~表10-11。
二齿差几何参数表见表10-12~表10-15。
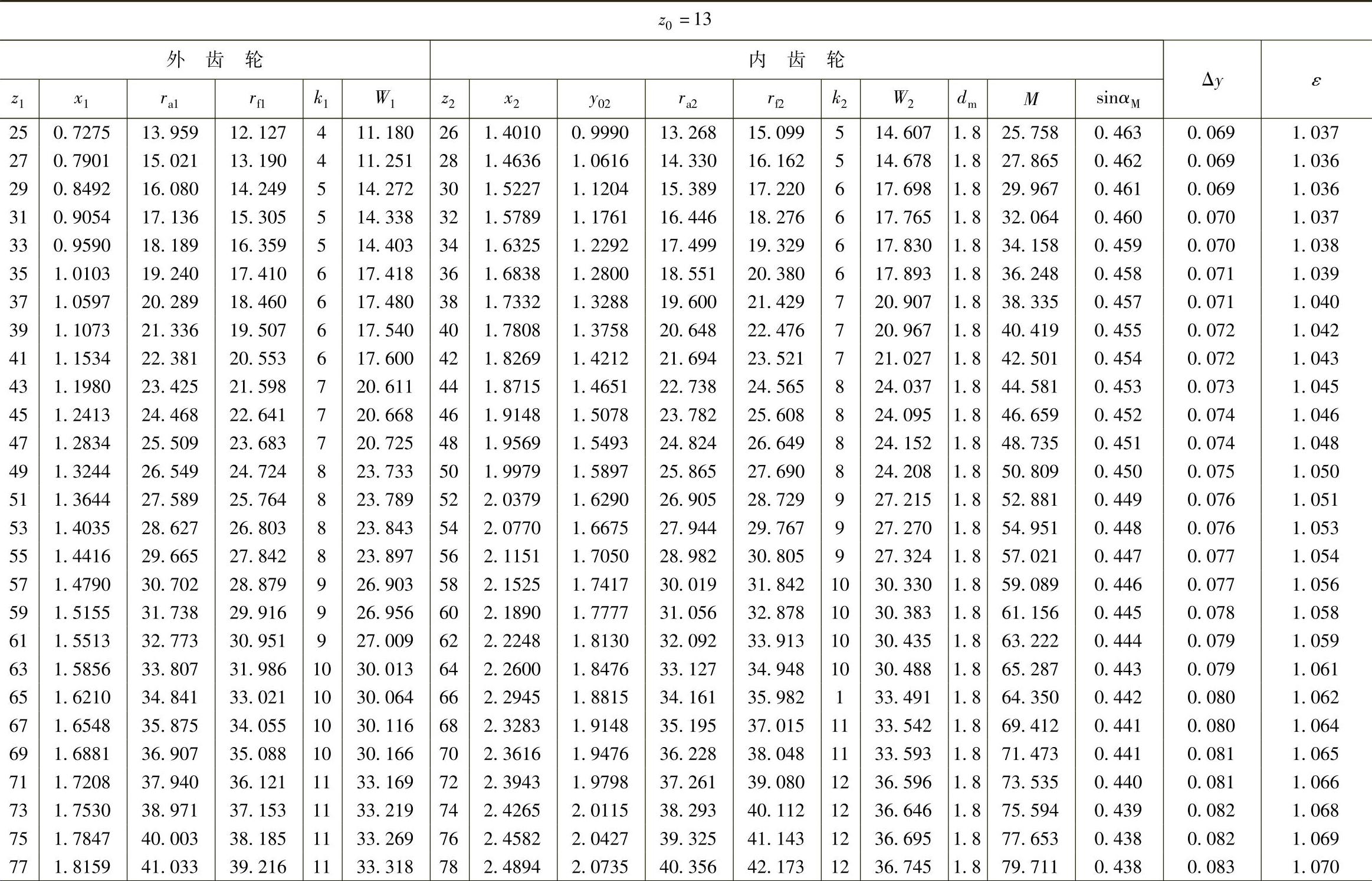
表10 - 6 一齿差几何参数表(z0=13,α′=55᥊9898°,a′=0᥊84)
(续)
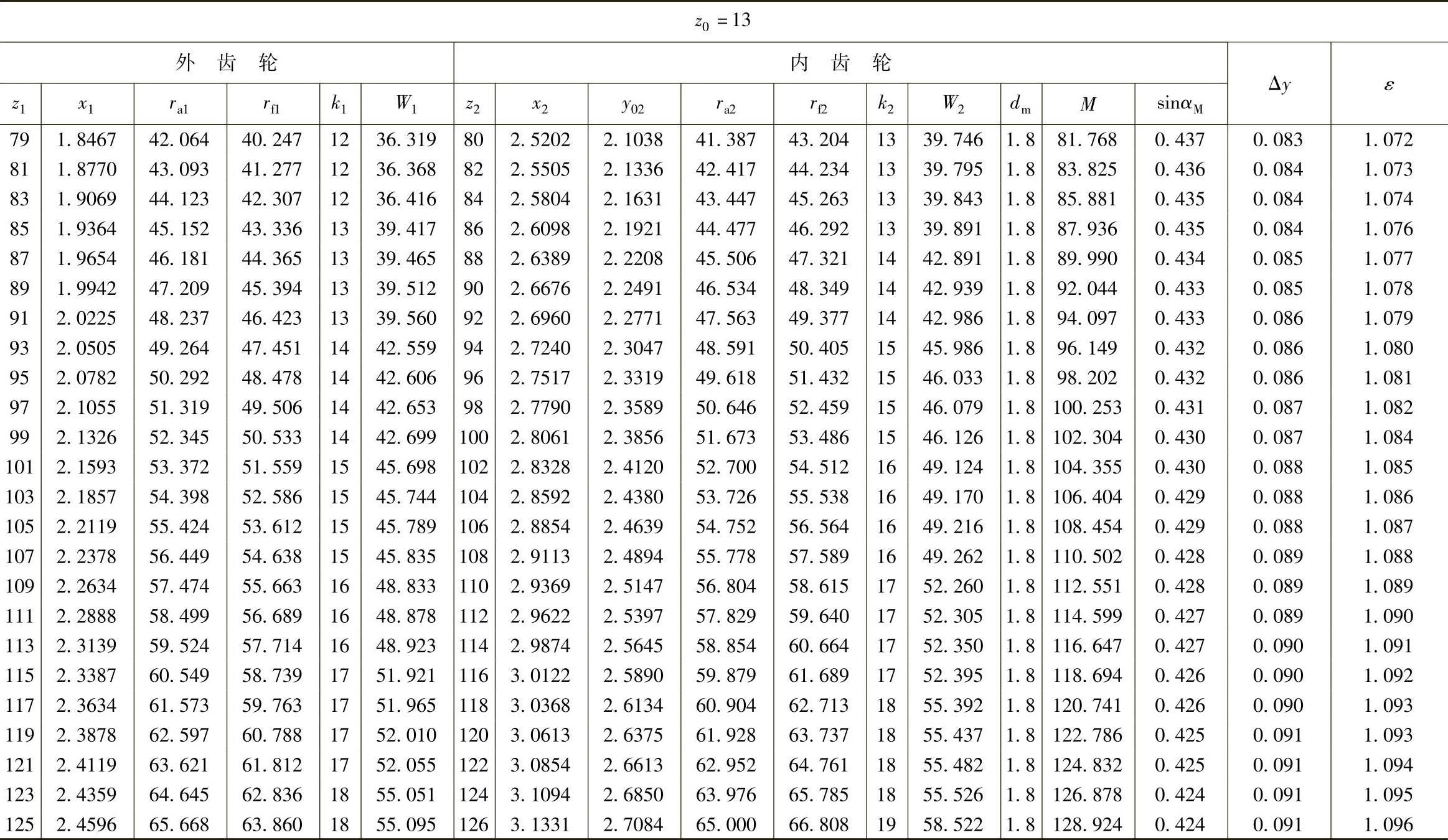
注1.参数表数值虽以x0=0计算的,但加工齿轮时不受此限。
2
.当模数m≠1时,参数表中ra1、rf1、W1、ra2、rf2、W2、dm、M等值均应乘以模数m,中心距a′也应乘以模数m;
3.sinαM值供计算量柱距的偏差与公差用。
表10 - 7 一齿差几何参数表(z0=17,α′=55᥊9898°,a′=0᥊84)
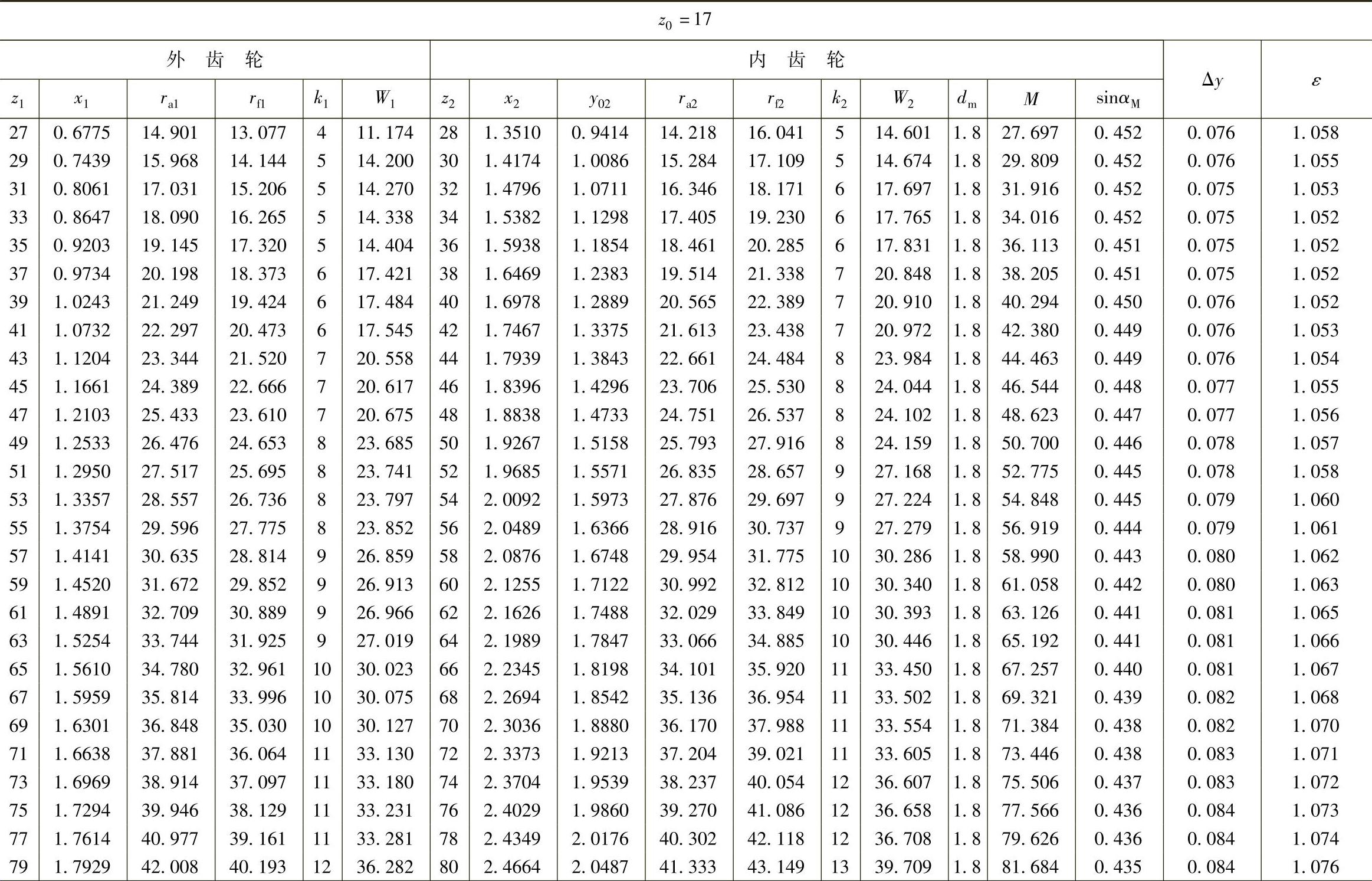
(续)
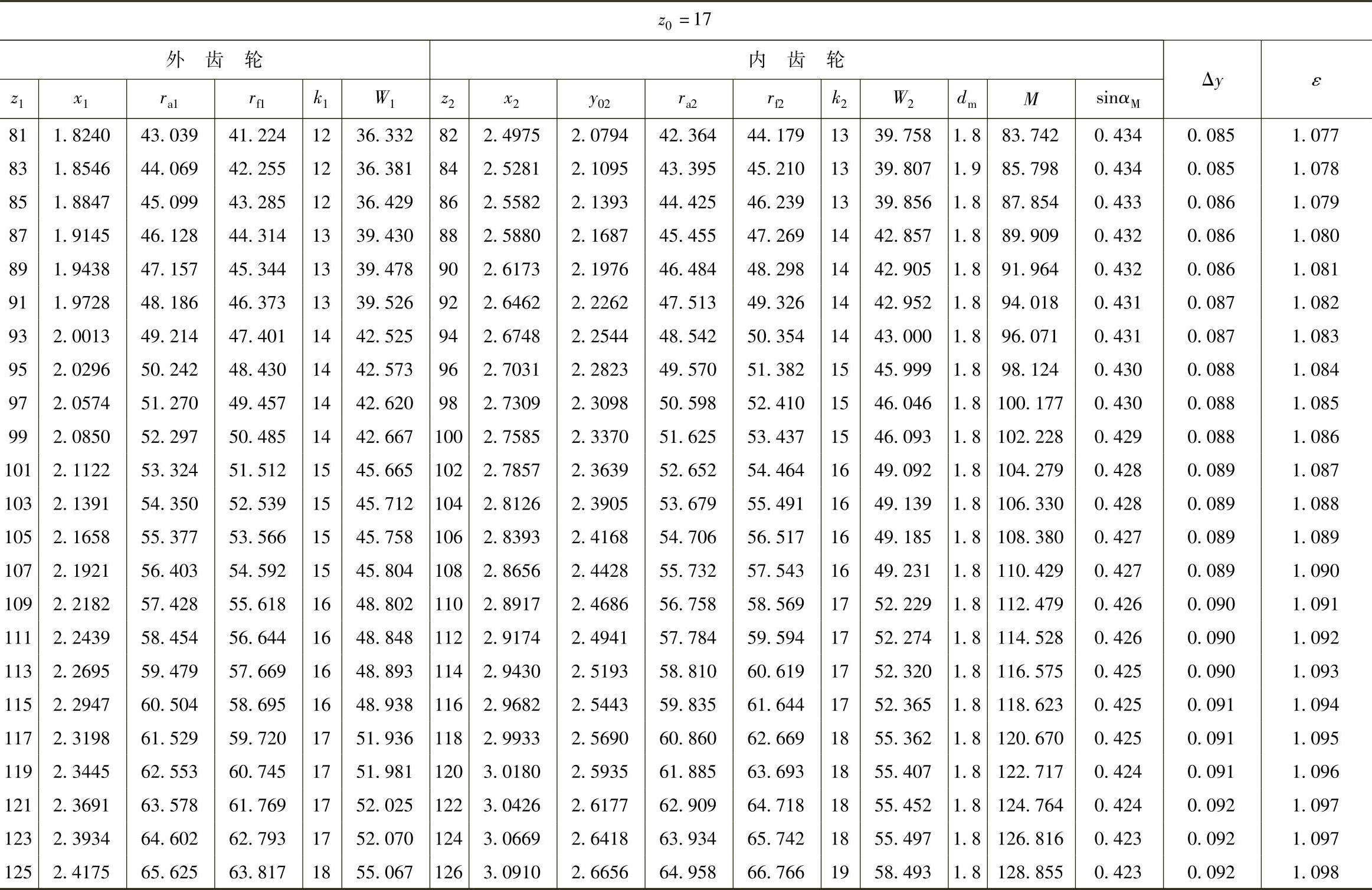
表10 - 8 一齿差几何参数表(z0=20,α′=55᥊9898°,a′=0᥊84)
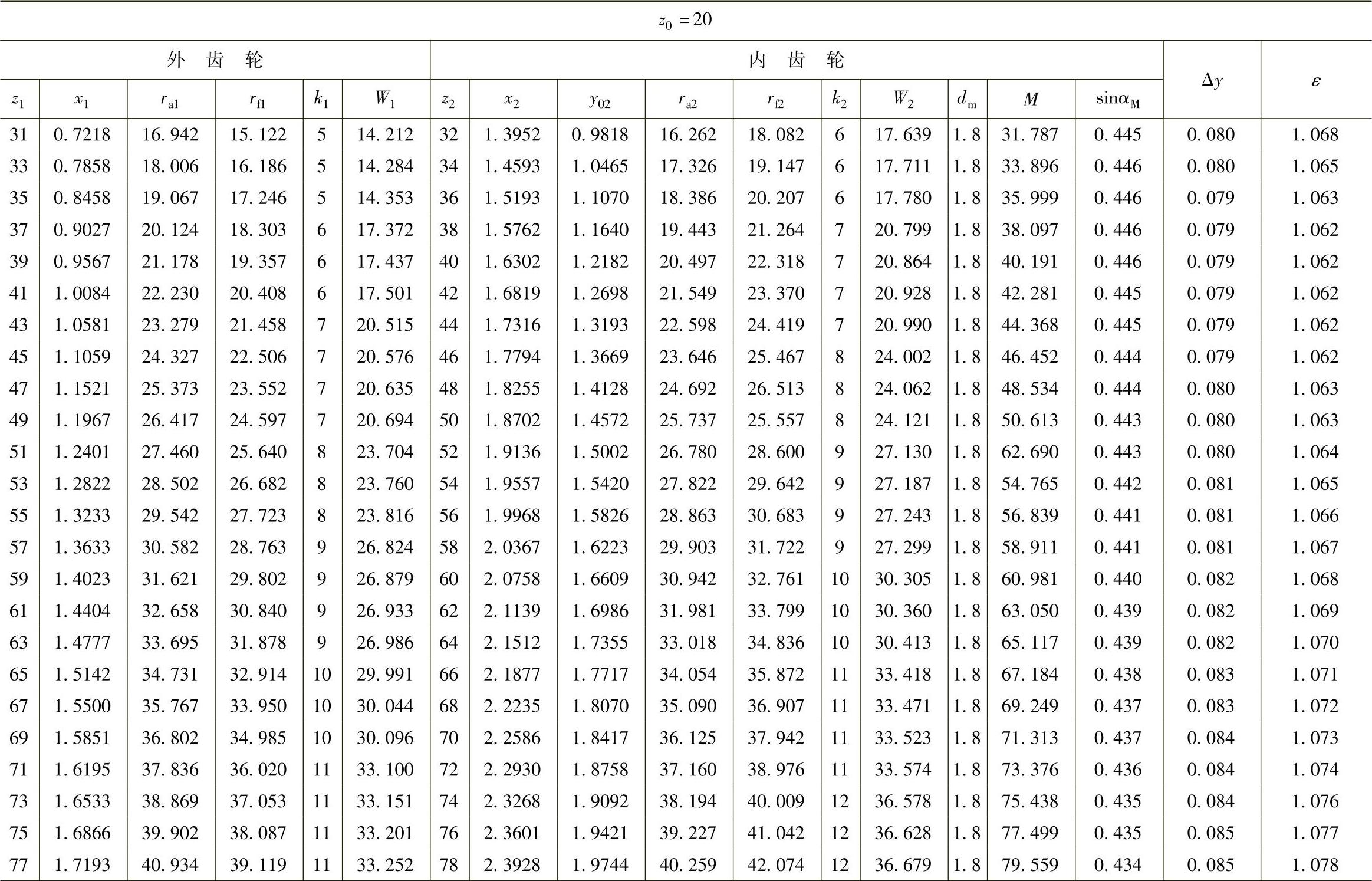
(续)
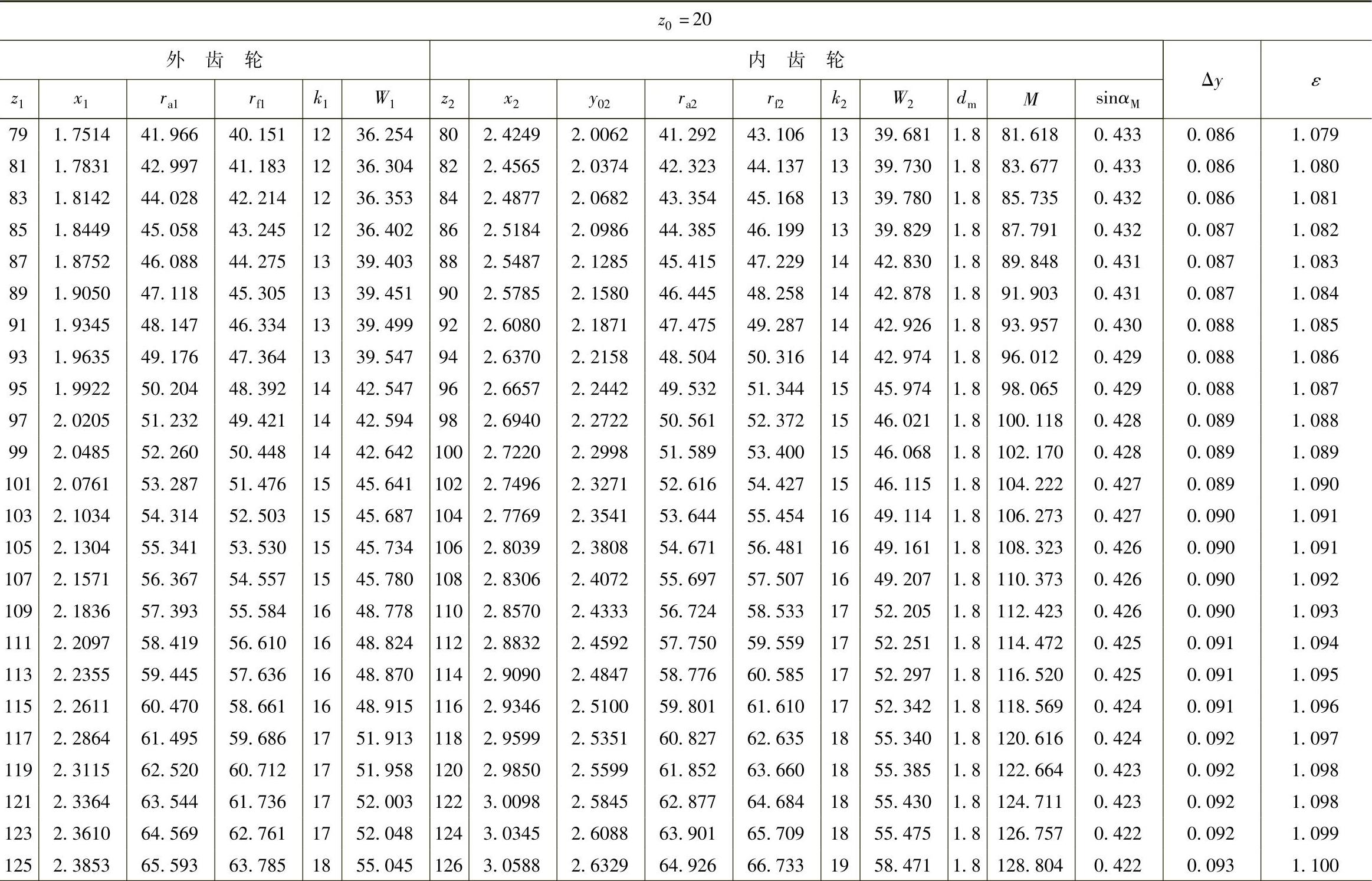
表10 - 9 一齿差几何参数表(z0=25,α′=55᥊9898°,a′=0᥊84)
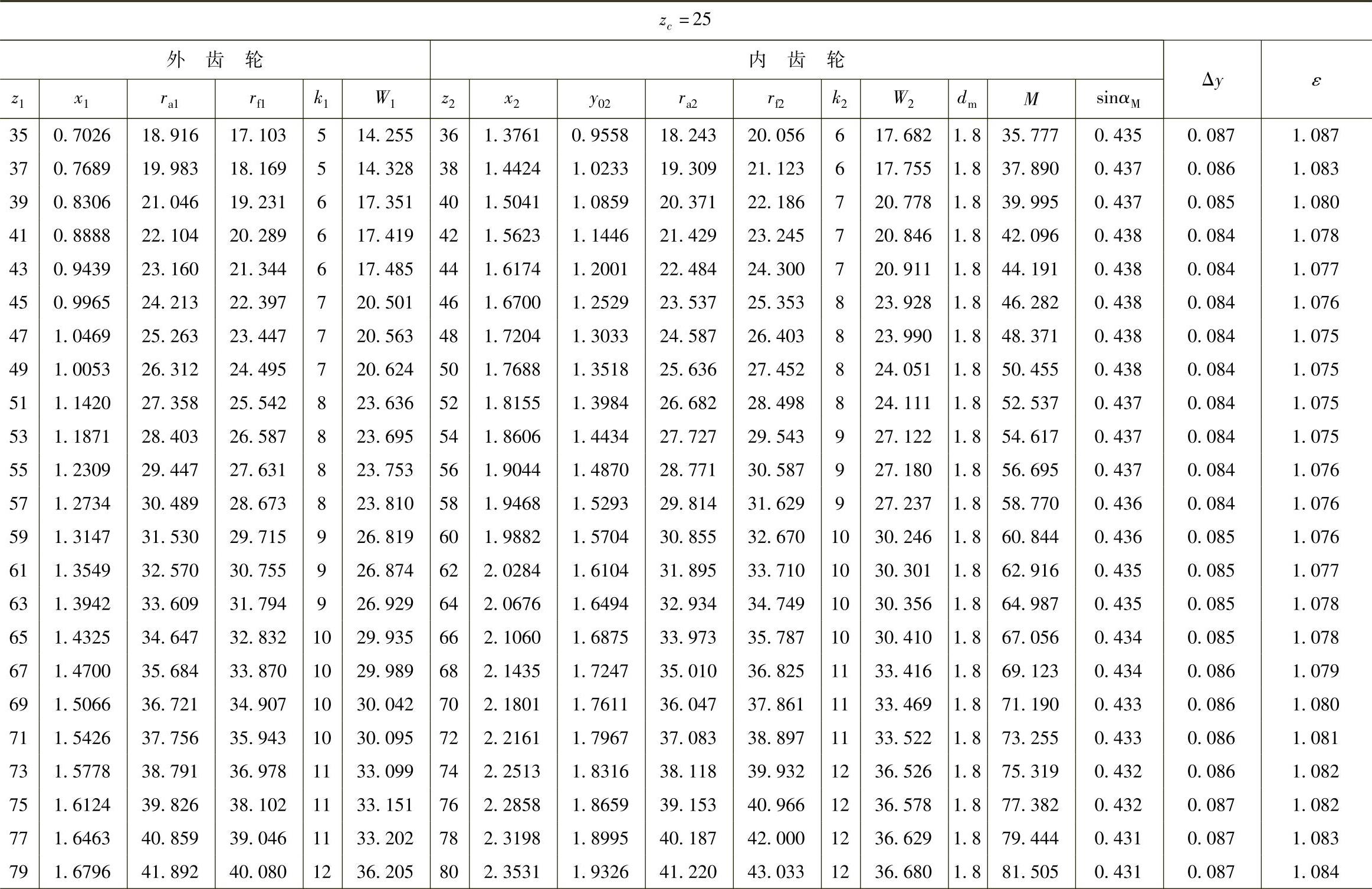
(续)
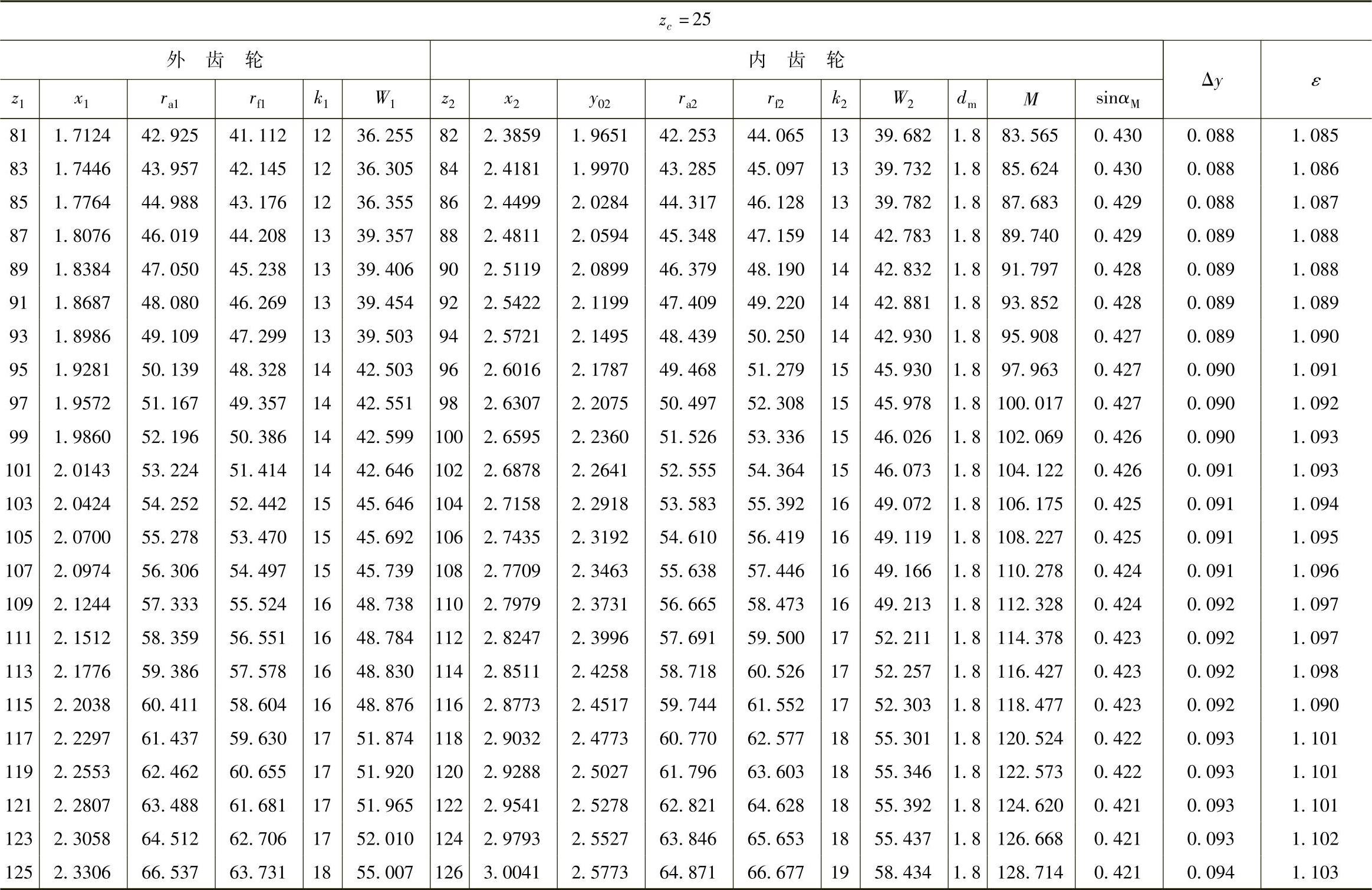
表10 - 10 一齿差几何参数表(z0=34,α′=55᥊9898°,a′=0᥊84)
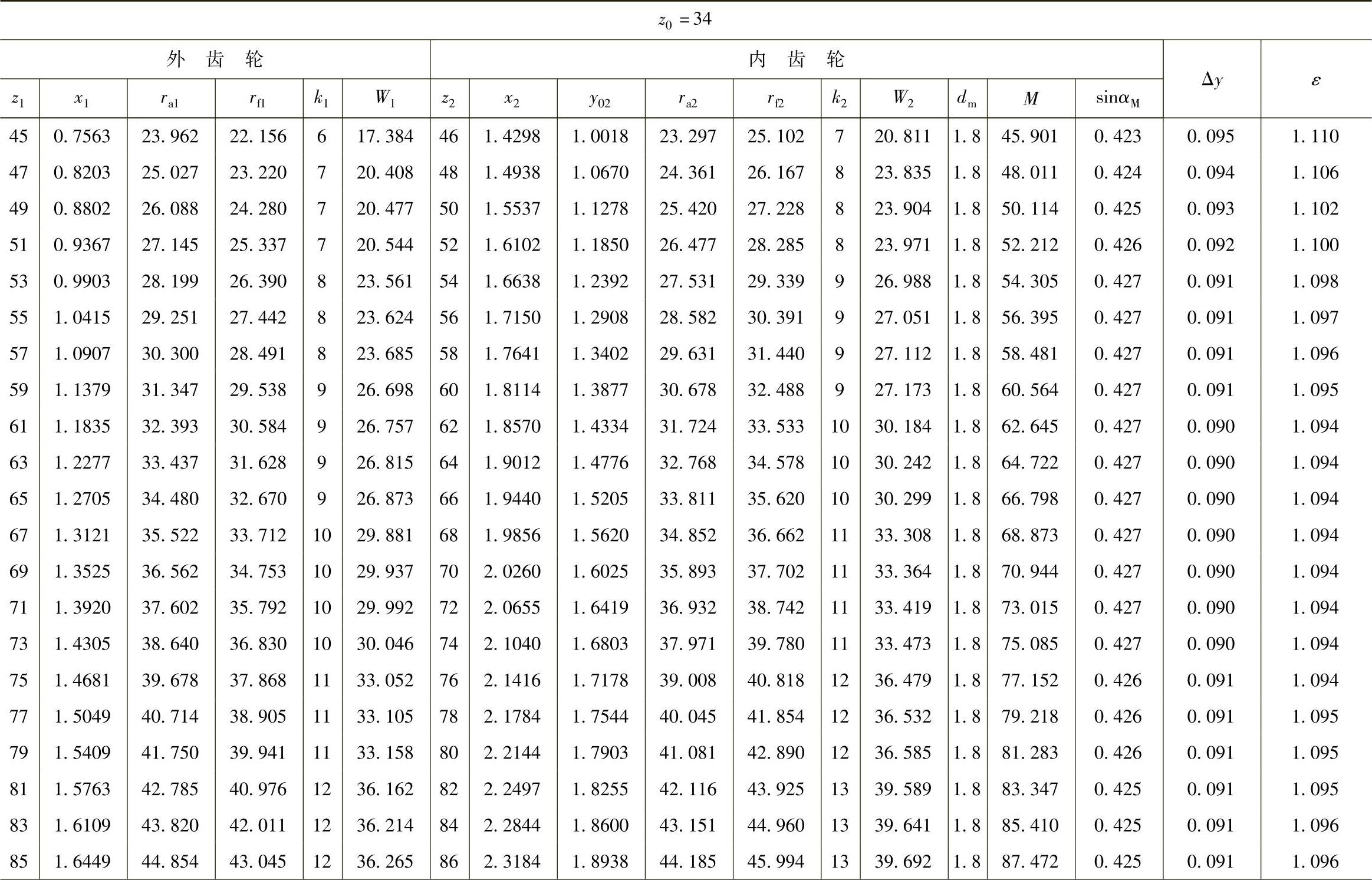
(续)
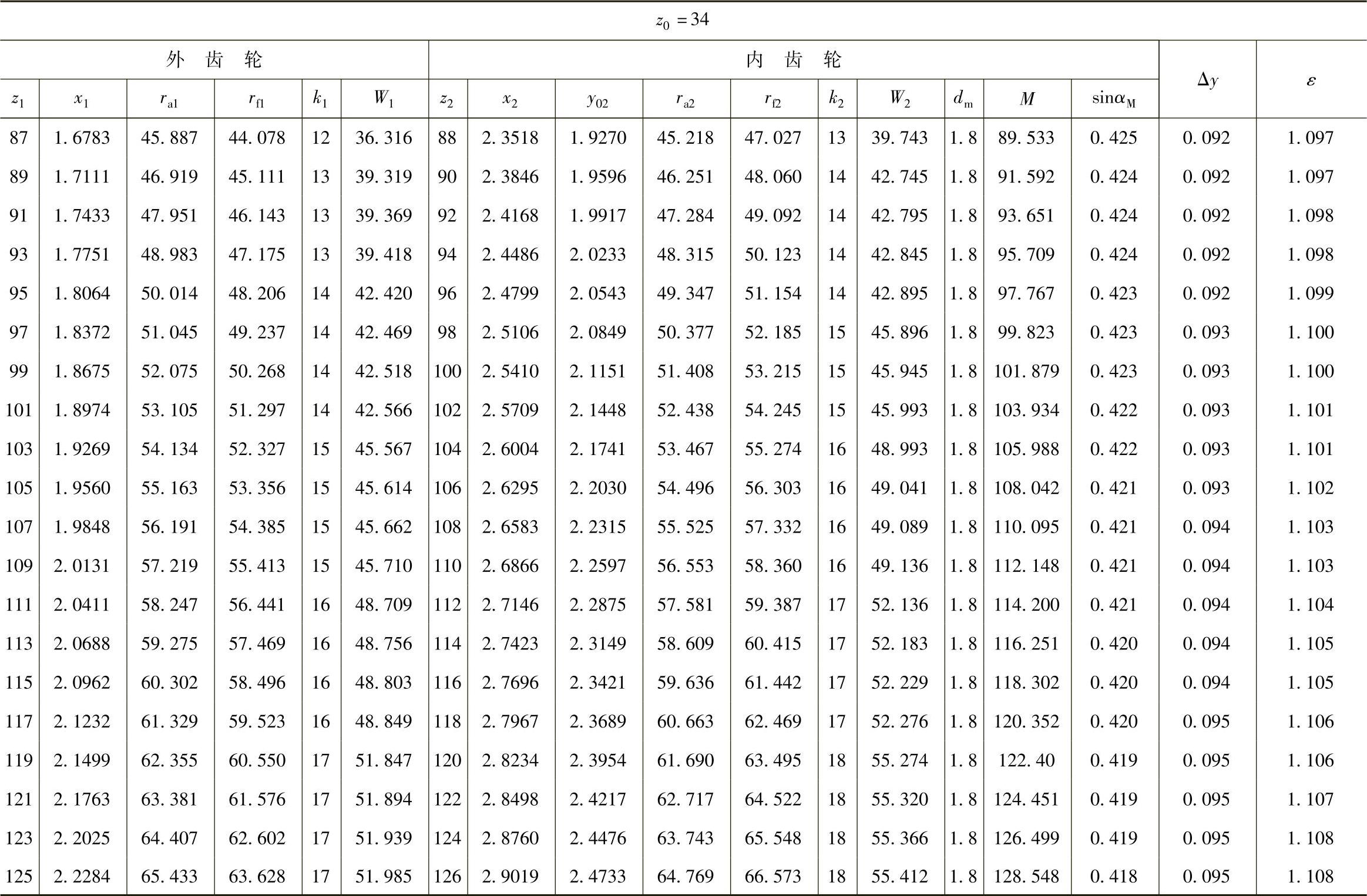
表10 - 11 一齿差几何参数表(z0=50,α′=55᥊9898°,a′=0᥊84)
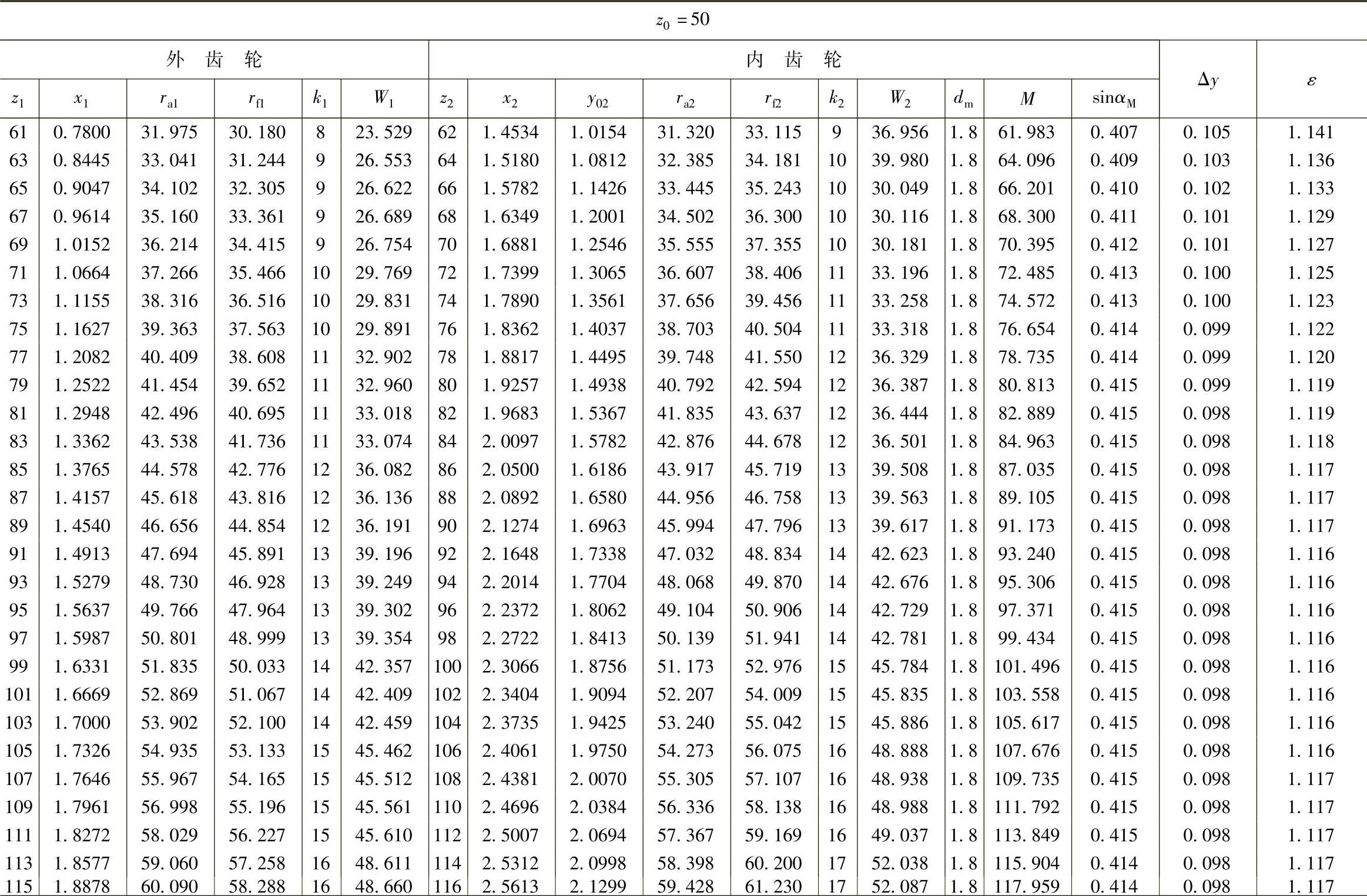
(续)

表10 - 12 二齿差几何参数表(z0=20,α′=39᥊0492°,a′=1᥊21)
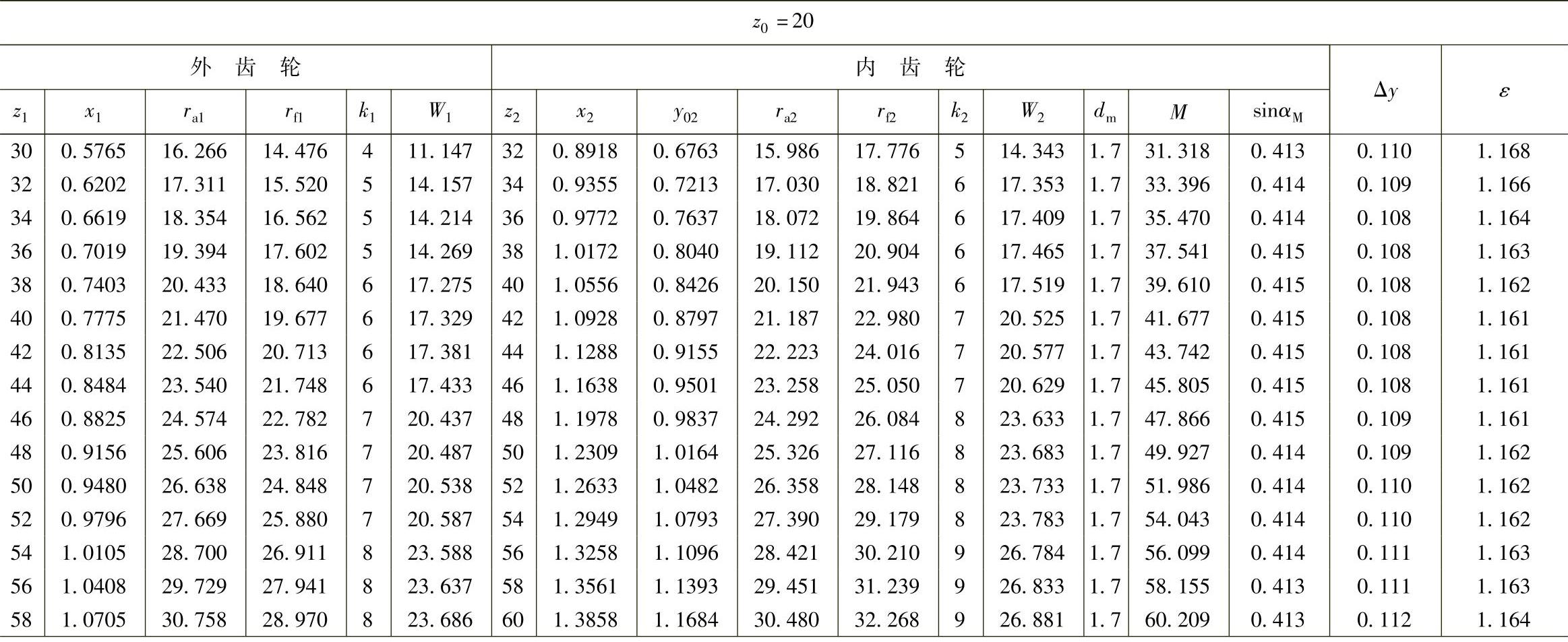
(续)
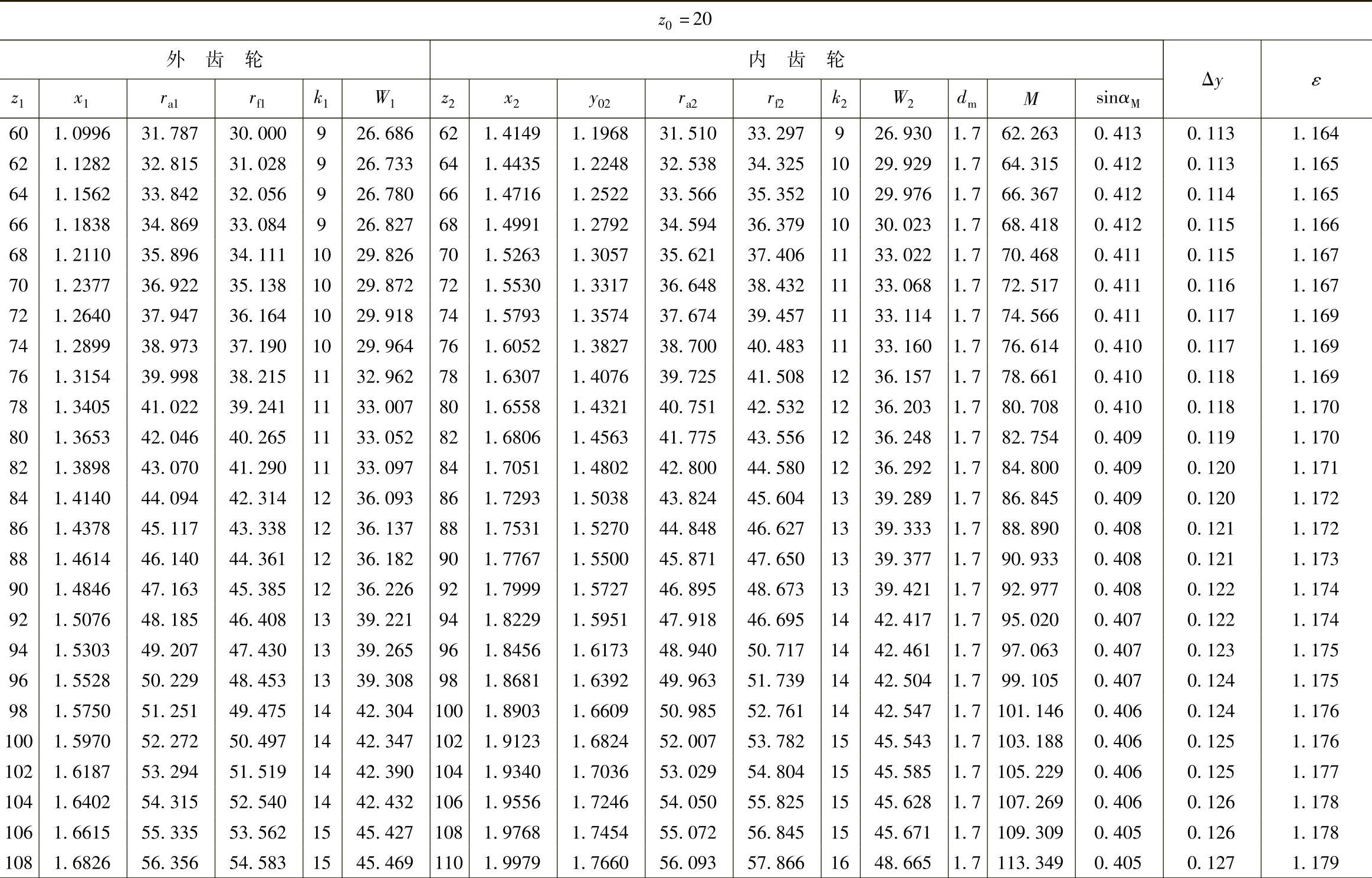
(续)

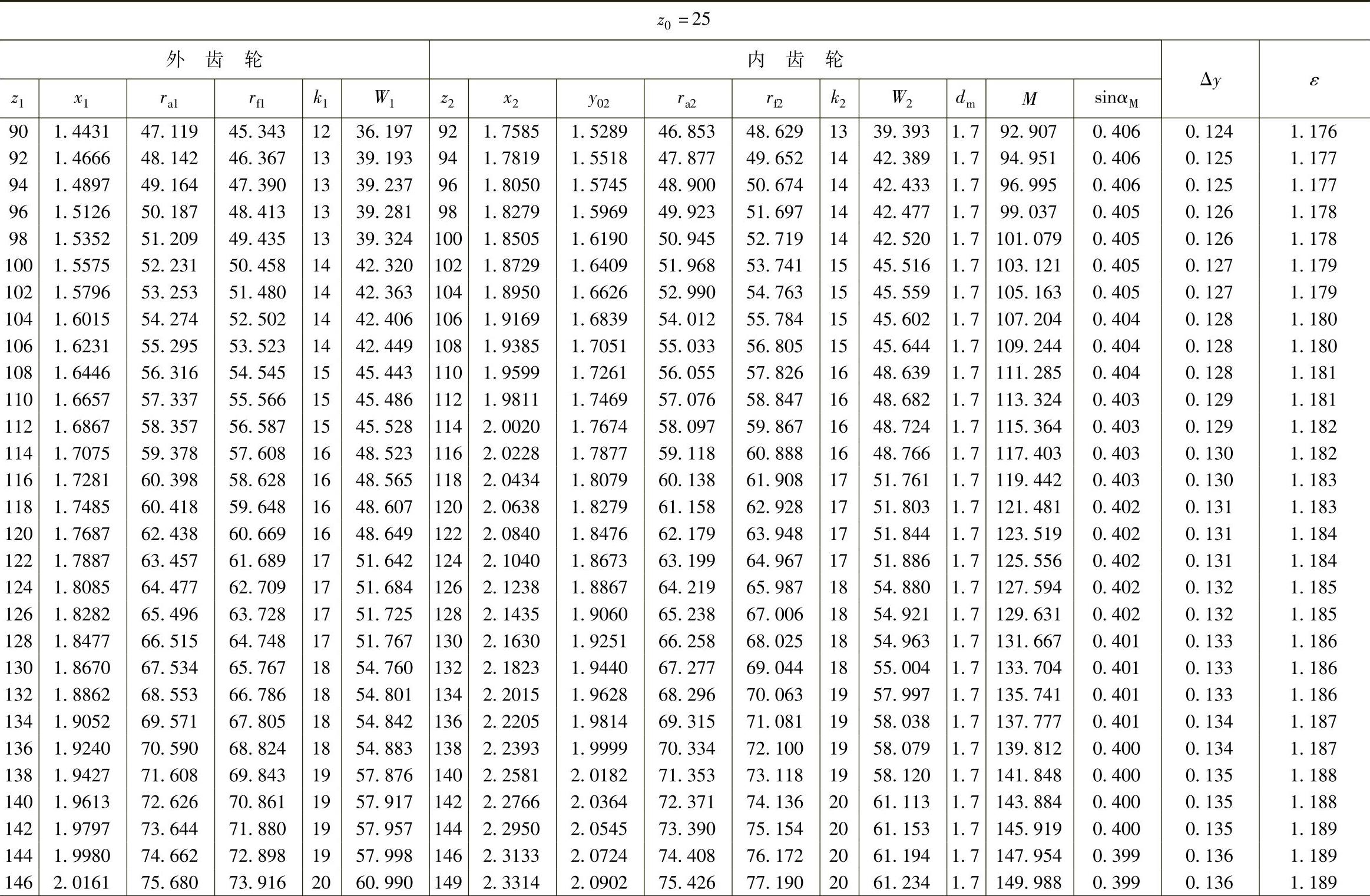
表10 - 13 二齿差几何参数表(z0=25,α′=39᥊0492°,a′=1᥊21)
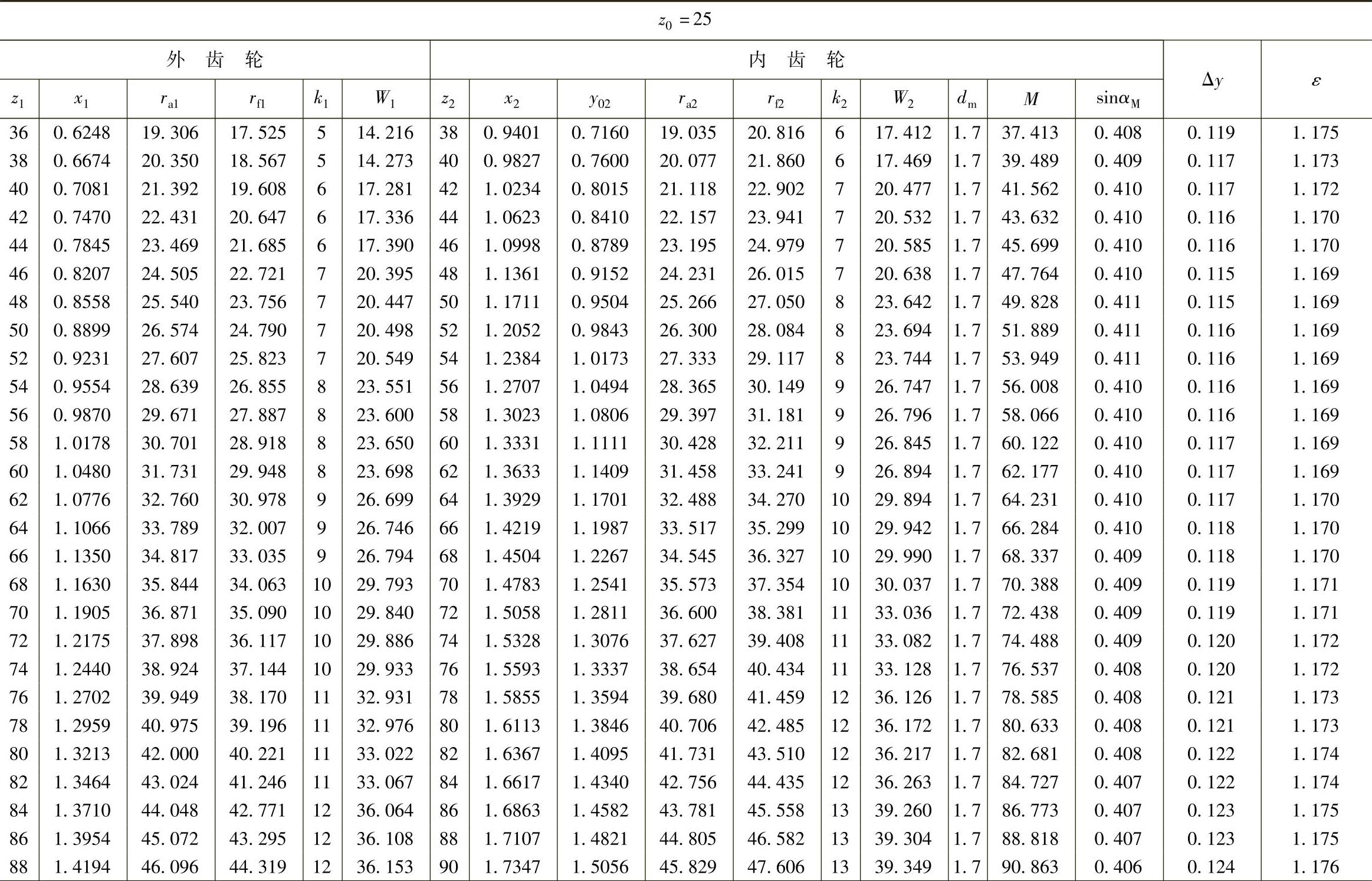
(续)
(续)
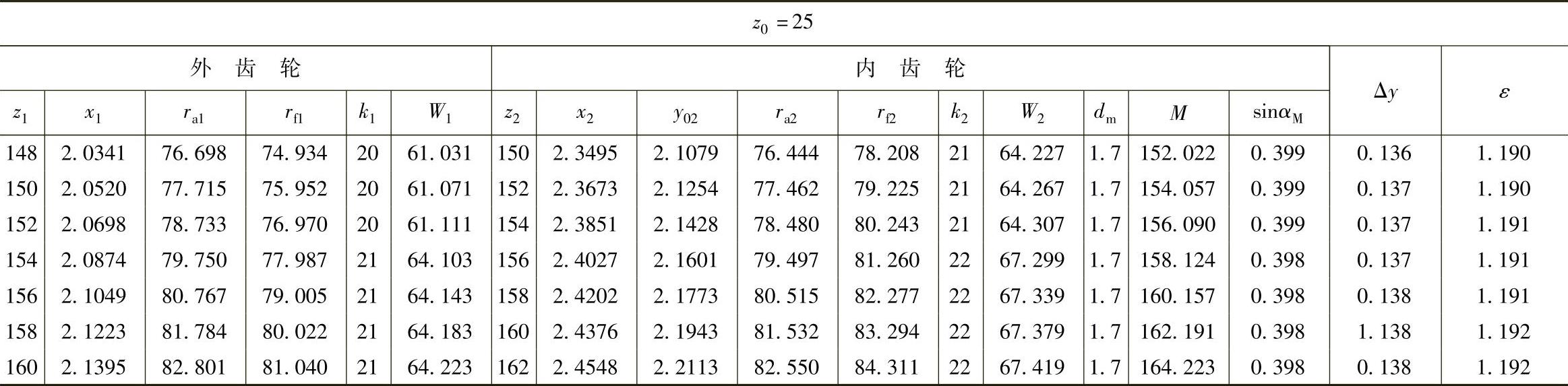
表10 - 14 二齿差几何参数表(z0=34,α′=39᥊0492°,a′=1᥊21)
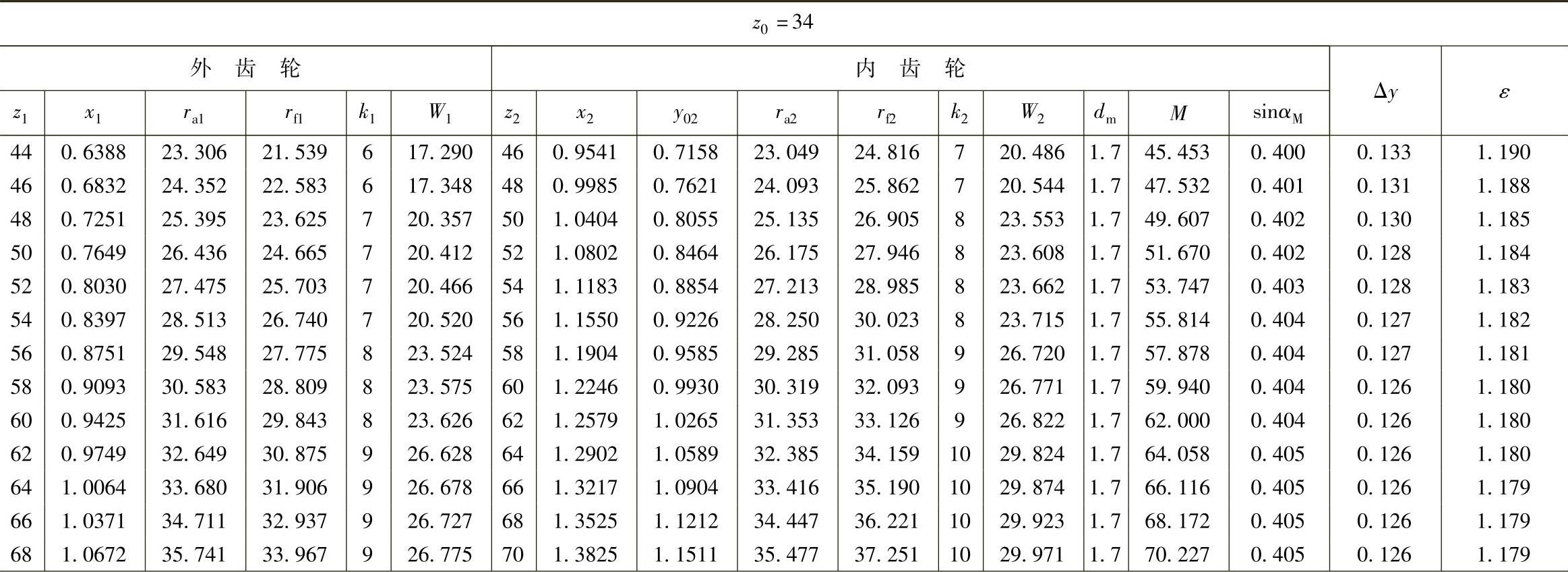
(续)
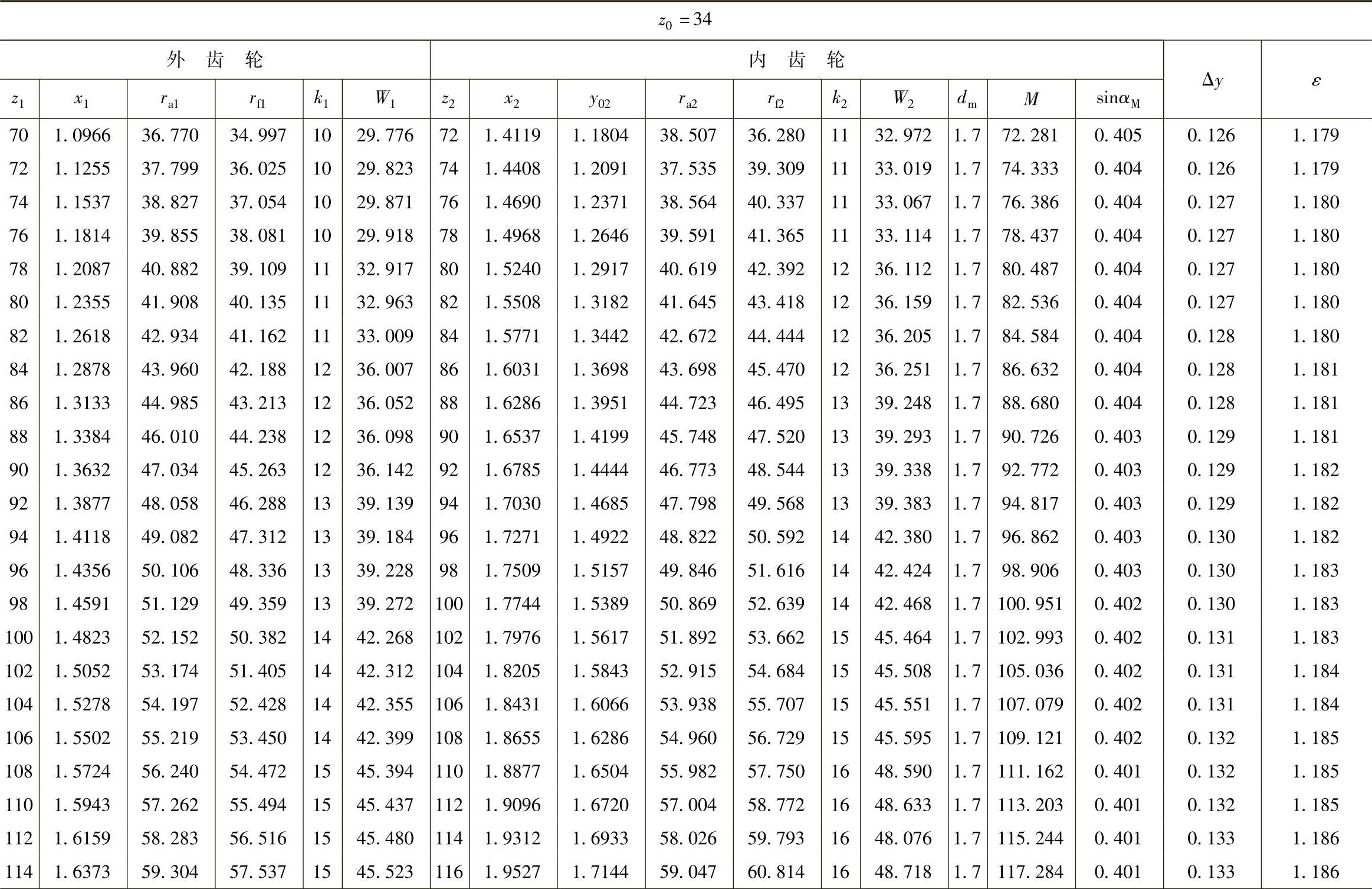
(续)
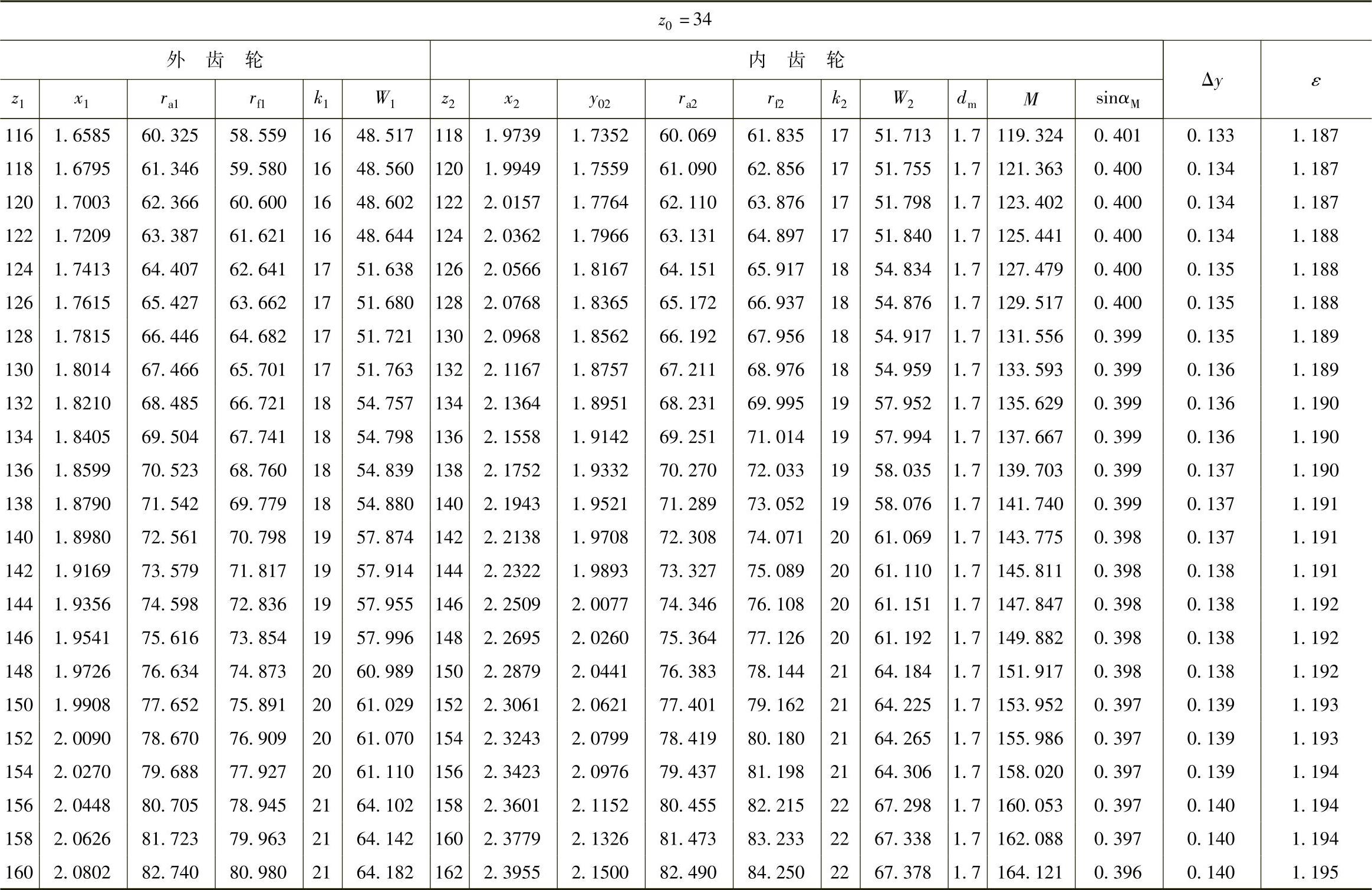
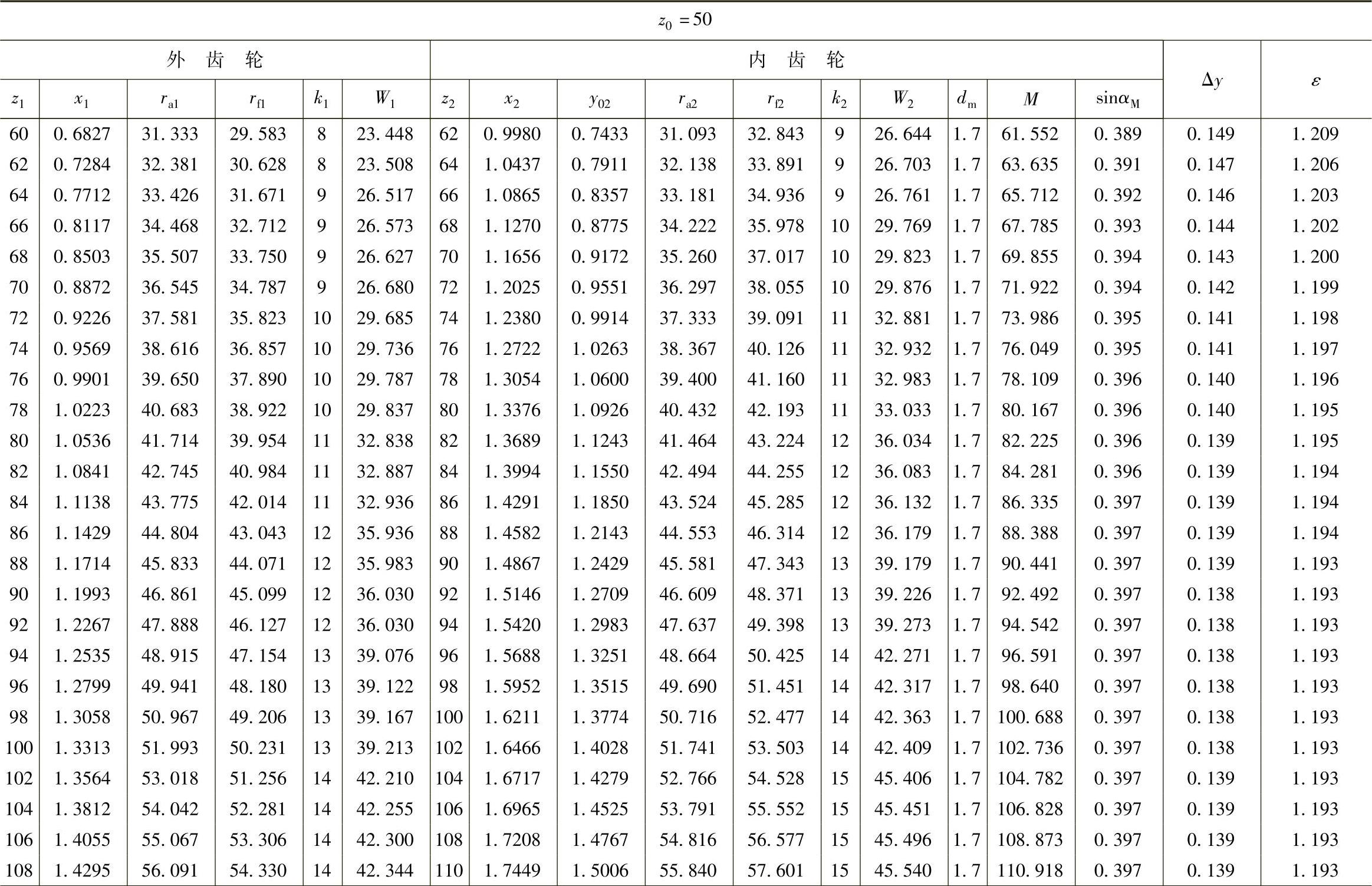
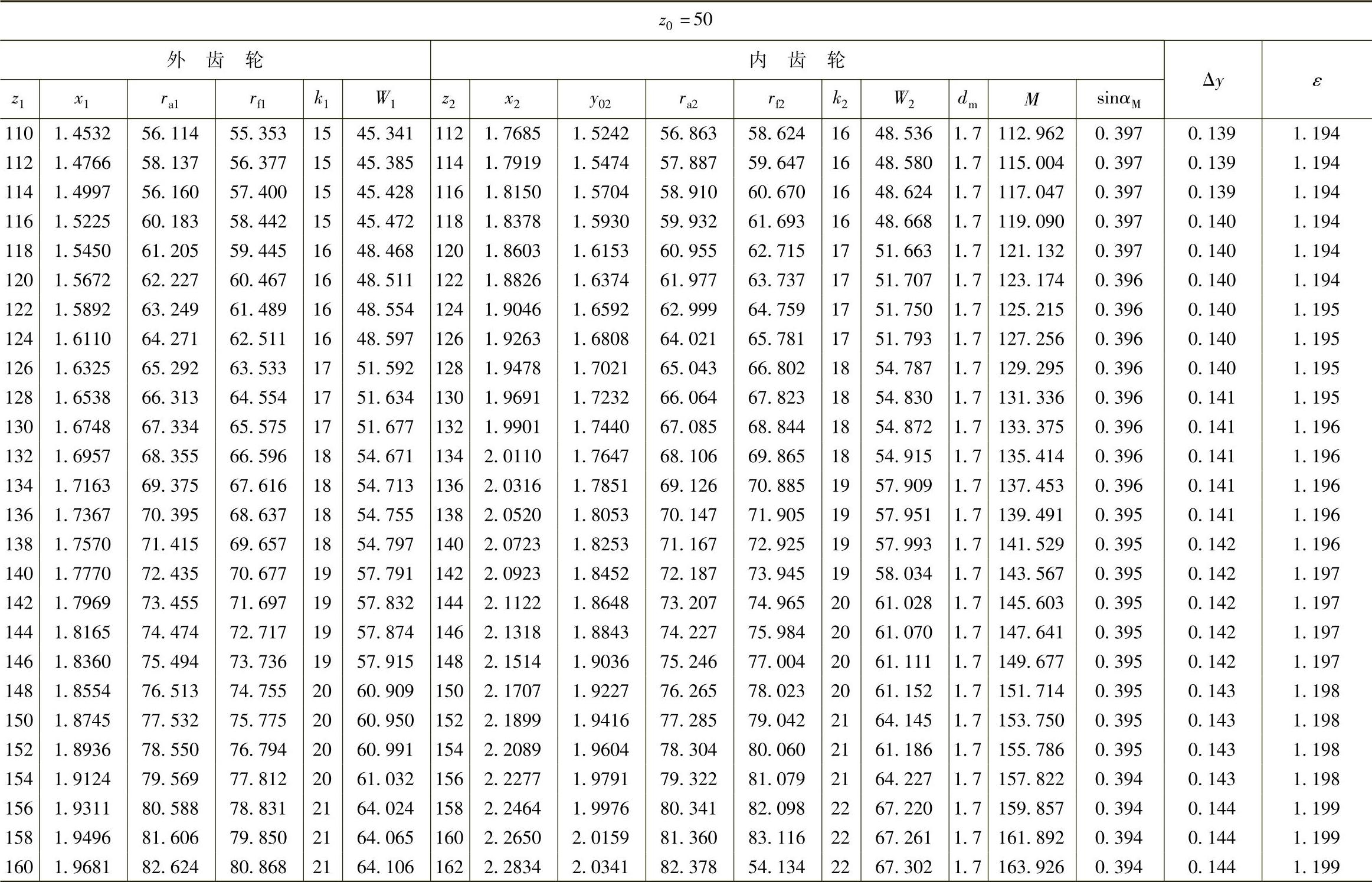
表10 - 15 二齿差几何参数表(z0=50,α′=39᥊0492°,a′=1᥊21)
(续)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






