在图9-1a所示的3K型行星齿轮传动中，a、b、e为三个外伸轴，b为固定件，现在要求轮a主动，轮e从动时，轮系的效率η^b_ae。应用效率计算的普遍式（8-158），如果已知η^e_ab（将原式中的H改成e），η^b_ae就可求得。但在一般情况η^e_ab也是未知数，为此，对这种轮系应重新推导公式，与前述相同可写出

下面再分析对H作相对运动后，轮a、b和e三者传递的功率P^H_a、P_b^H及P^H_e间的关系。在新的转化机构中，H可看作固定件，但a、b、e中哪一个为主动件还要分析一下，与前相同，根据功率正、负来确定主、从动。若P^H_a>0，则在转化机构中轮a为主动，否则为从动。轮e也是这样，根据P^H_e的正、负来确定主、从动。如在转化机构中轮a、e主动，轮b从动，则

P_a^HηHab+PHe ηeHb+PHb=0

即

T_an_a^HηHab+Te ηHe ηHeb+Tb nbH=0 （9-23）

联解式（9-20）、式（9-23），即可求得η^b_ae与η^b_ea同η^H的关系式。如在转化机构中，轮a、e从动，轮b为主动，则

然后联解式（9-19）、式（9-20）、式（9-21）和式（9-23）。轮a、b、e三者在转化机构中的主从关系，还可有其他各种形式，分析方法类同，这里的关键问题是如何确定轮a、b、e中哪个主动，哪个从动。而式（8-158）是通过i^a_Hb的正、负来判定轮a的主、从动的，其中H是转化机构的固定件。现在类似地用i^a_Hb和i^e_Hb来判定H固定时轮a和轮e的主动、从动；若i^a_Hb＞0，则当固定件由b改变为H时，轮a不变其主从关系。反之，若i^a_Hb＜0，则轮a原先主动就变成从动，原先从动就变成主动。同理，若i^e_Hb＞0，则当固定件由b改变为H时，轮e不变其主从关系，反之就改变。

下面具体分析一下3K型行星齿轮传动的效率。

1）固定件d_b＞d_e此时由于，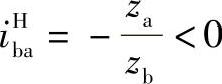

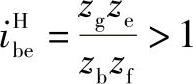
所以

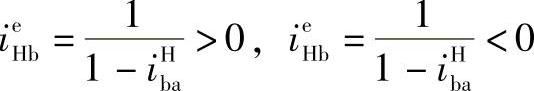
若在行星轮系中，轮a主动，轮b从动，则在转化机构中轮a、e都变为主动，啮合功率的传递路线为

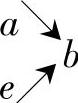，从而得到式（9-23）。将其与式（9-20）和式（9-22）联解，可得

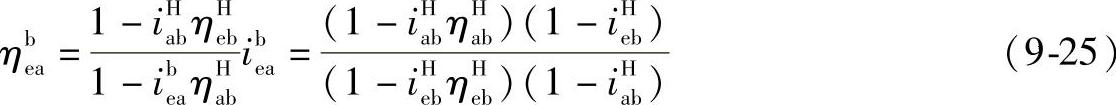
若在行星轮系中，轮e主动，轮a主动，则在转化机构中轮a、e都变为从动，啮合功率的传递路线为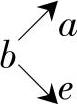，从而得到式（9-24）。将其与式（9-21）和式（9-22）联解，可得

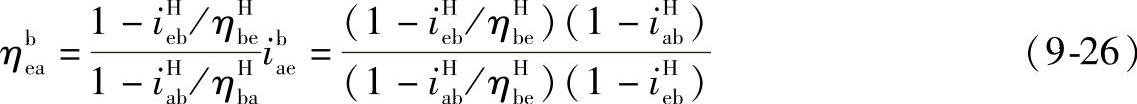
取η_b^He=η^H_eb，η_b^Ha=η^H_ab，则式（9-25）、式（9-26）可写成统一式

当轮a主动时，β=1；轮a为从动时，β=-1。η^H_ab、η^H_eb是H固定时转化机构变成一定轴轮系所对应的啮合效率。

2）固定件d_b＜d_e此时，由于,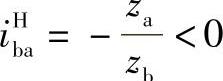

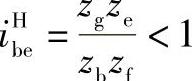
所以

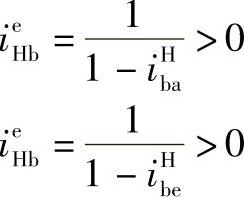
若在行星轮系中轮a主动，轮e从动，则在转化机构中仍是轮a主动，轮e从动。至于轮b是主动还是从动，可用下面方法进行分析。回顾式（8-155）的分析过程，曾推得i^a_Hb=P^H_a/P^b_a的关系，同样也可推得i^a_Hb=P^H_a/P^b_a及i^e_Hb=P^H_c/P^b_c。由于i^a_Hb＜1，i^e_Hb＞1，所以P_e^H/P^b_e＞P^H_a/P^b_a。如果略去摩擦损失的话，P^b_e=P^b_a，所以得P^H_e＞P^H_a。这就是说在转化机构中，从动件轮e传递功率的绝对值要比主动件轮a传递功率的绝对值大。因此，轮b必定也是主动件，啮合功率传递为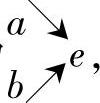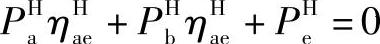它们的关系为

T_ana^HηHae+Tb nbH ηHbe+Te nHe=0

将上式与式（9-20）和式（9-22）联解，可得

若在行星轮系中，轮e主动，轮a从动，则在转化机构中仍是轮e主动，轮a从动。此时根据P^H_e＞P^H_a，由于主动件轮e传递的功率大，故轮b必定为从动，啮合功率传递的路线变成它们之间的关系为

T_an^H_a/η^H_ea+Tb n_b^H/η^H_eb+Ten^H_e=0

将上式与式（9-21）、式（9-22）联解，可得

取η^H_eb=η^H_be，η^H_ea=η^H_ae，则式（9-28）和式（9-29）可统一为

以上将3K型行星齿轮传动的两个效率计算公式，式（9-27）、式（9-30），分别用于d_b>d_e和d_b<d_e的两种情况。

3）改变结构后 将图9-1a所示的3K型行星齿轮传动的结构改一下，即将其中轮a从轮b这一排移到轮e排上去，如图9-4所示，则由于

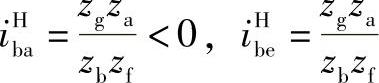
当d_b＞d_e时i_b^He＞1；当d_b＜d_e时，i_b^He＜1，所以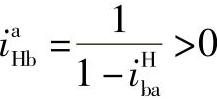

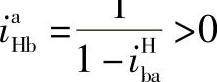
当d_b＞d_e时，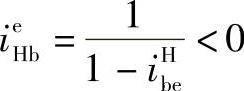

当d_b＜d_e时，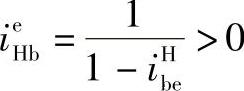

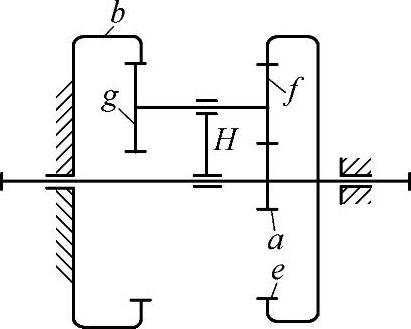
图9-4 3K（NGWN）型行星齿轮传动

因此，式（9-27）和式（9-30）两式同样适用，而不必像前苏联B.H.库特略夫采夫（B.H.Kудрявцев）那样用了8个公式计算3K型行星齿轮传动的效率，使人感到繁琐，而又不得要领。综上所述，可得到如下结论：3K型行星齿轮传动的效率计算，可以根据两个内齿轮固定的是大轮还是小轮而分别用式（9-27）或式（9-30）进行计算，不必考虑带外伸轴的小齿轮位于哪一排。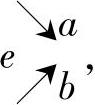

4）下面论述几个问题3K型行星轮系的效率可否像运动分析那样拆成两个部分计算？两个内齿轮中要固定一个，究竟固定大的好还是固定小的好？小齿轮a究竟放在b排好还是放在e排好？即图9-1a与图9-5哪一种结构好？我们将逐个论述这些问题。(www.daowen.com)

3K型行星轮系可以变成两个2K-H型串联的行星轮系，其传动比不变，如图9-1a所示的轮系可用图9-5所示的轮系来代替，则

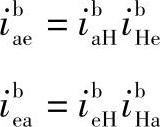
至于效率是否也可以这样代替，而写成

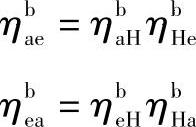
回答是要看一下固定的内齿轮b是大轮还是小轮，如果d′_b＞d′_e，则上述的式子是成立的，否则就不成立，也就是说不能代替。国内外有些资料，对这个问题的论述是错误的，在前苏联库氏的1977年版《行星齿轮传动手册》中，也没有明确指出这个问题。要证明这一点也不难，因为前面已经分析了这两种情况。首先当d_b＞d_e，啮合功率是在a、b与e、b之间传递，这与图9-5的情况是吻合的。通过图9-5所示轮系的效率计算，也证明某结果与式（9-26）相同。但是，当d_b＜d_e时，啮合功率是在a、e与b、e之间传递，a、b之间没有直接关系，因此与图9-5就不一致。通过具体的效率计算也可得到证明，这里不作详细论证。于是，可得如下结论：

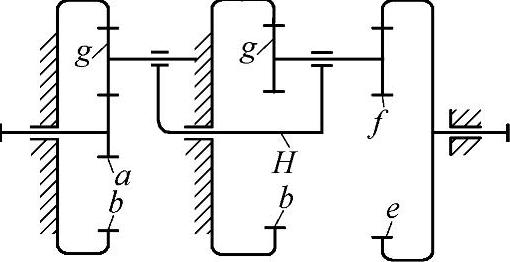
图9-5 把图9-1a 3K型分解为两个2K-H型的串联

3K型行星轮系的效率计算，当大内齿轮固定时与传动比计算一样，可用两个串联的2K-H型行星轮系来代替；如果固定的是小内齿轮，则这样计算是错误的。

对于3K型行星轮系，一般用于传动比较大处，希望效率也较高。当d_b>d_e时，轮b固定和轮e固定两种轮系的效率关系，可应用效率普遍式来表达如下：

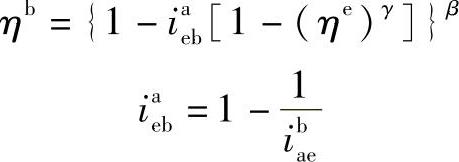
而i^b_ae=i^b_aHi^h_He=（1-i^H_ab）（1-i^e_Hb）。由前面分析可知，当d_b＞d_e时，i^H_ab＜0，i^e_Hb＜0，所以i^b_ae＞1，i^a_eb＞0。于是当a主动时，β=+1，γ=+1；a从动时，β=-1，γ=-1。

所以

或

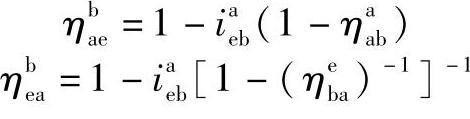
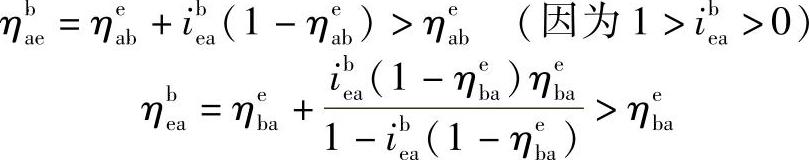
此外

i^b_ae=1-i^e_ab=1+i^a_eb　（因为i^e_ab=1-i^b_ae<0）。所以，3K型行星轮系当大内齿轮固定时不仅传动比大，而且效率也比小内齿轮固定时高。

再对比一下图9-1a和图9-4所示的两种结构究竟哪一种好？即轮a放在b排上好还是e排上好？首先从传动比来看，用齿数来表达

这里为了便于比较，令两种结构的a、b、e都相同，f、g就不能相同，为此将图9-4中的f与g改成f′与g′。从上面公式很难看出图9-1a与图9-4两种结构哪一种传动比i^b_ae较大。如果采用图解法，当给出相同的转速n_a时，在对应的啮合点上具有相同的速度v_A和v_e，如图9-6所示（其中图9-6a即为图9-1a，图9-6b即为图9-4）。从而可以看出n_e也必相同（两者的、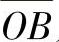及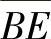距离都相同），所以i^b_ae或i^b_ea也是相同的。从轮齿的强度来看，两者外啮合齿轮副的接触强度不同。图9-6b中的a与f′比图9-6a中的a与g的中心距要小；而外啮合齿轮副恰恰是轮系中的薄弱环节，所以图9-6a即图9-1a结构的接触强度较好。

另外更重要的一点是图9-6b即图9-6结构的效率较低。其原因是负号机构与正号机构两部分传动比的分配不同，虽然两者的总传动比i^b_ae一样，但图9-6b的负号机构部分传动比下降，这对效率影响不大，而正号机构部分传动比增加引起效率下降，故图9-4是一种不妥当的设计。下面举一实例可以看得更清楚。

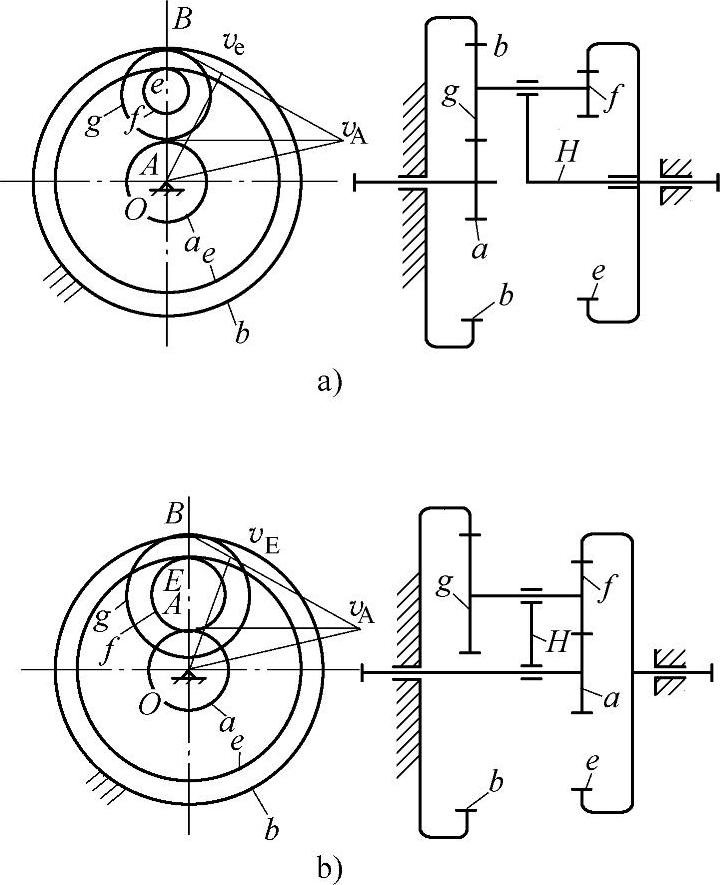
图9-6 3K型行星传动的变换

例9-4 已知3K型行星轮系z_a=20，z_b=140，z_e=130，z_f=50，z_g=60，根据两排齿轮的同心条件，可以求得z_f′=55，z_g′=65，取η^H_ab=0.97，η_e^Hb=0.98。试确定传动效率η^b_ae和ηbea。

解 当轮a与b同排时，

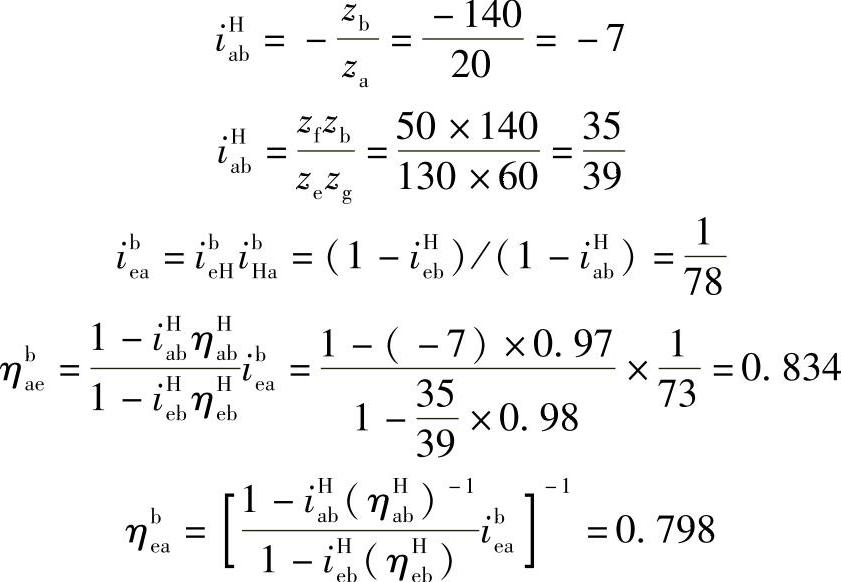
当轮a与e同排时，

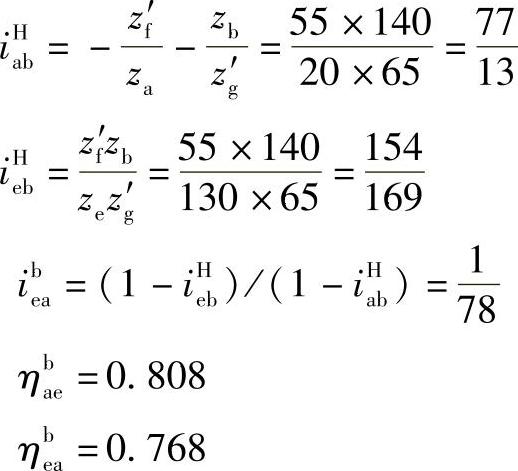
于是，得出如下两个结论：

①3K型行星轮系中，有三个外伸轴的齿轮a、b、e的大小如果保持不变，轮a与轮b同一排或者与轮e同一排，不影响轮系的传动比。

②3K型行星轮系的轮a建议放在固定的大内齿轮的同一排，这样在相同传动比的条件下，可获得较高的强度及较高的效率。

通常在估算或方案设计时，3K型行星传动的效率可直接从图9-7所示的线图查得。

应用实例：试确定i=154的3K型行星传动的效率。

根据表9-3得z_f=42，由图中查得η^b_ae=0.78。

对于3K型不同传动简图的效率计算式见表9-6。特殊3K型行星齿轮传动效率计算式见表9-7。

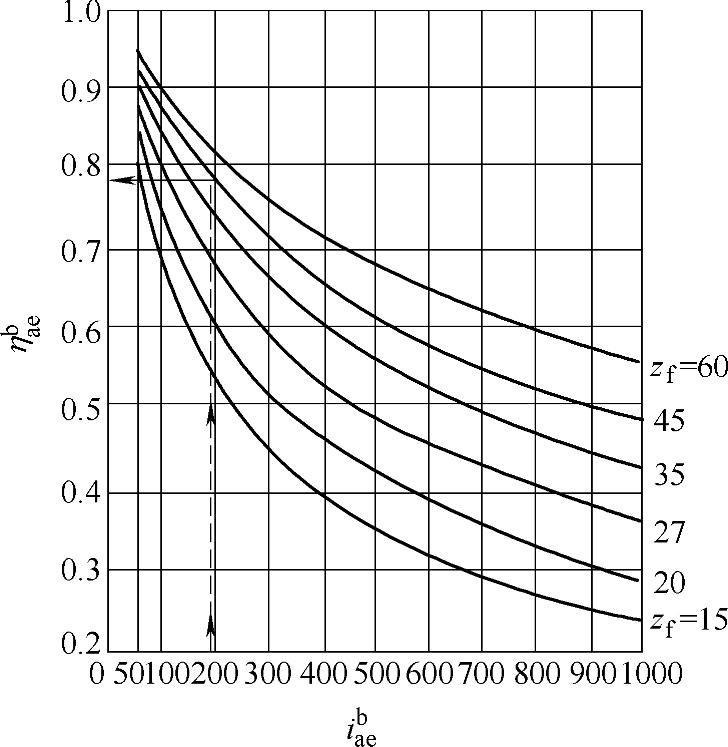
图9-7 当啮合中的摩擦因数_μ=0.12和行星轮滚动轴承中的当量摩擦因数_μT=0.006时，3K型（按简图9-1a设计的）行星减速器的效率

表9-6 3K（NGWN）型行星传动效率计算式

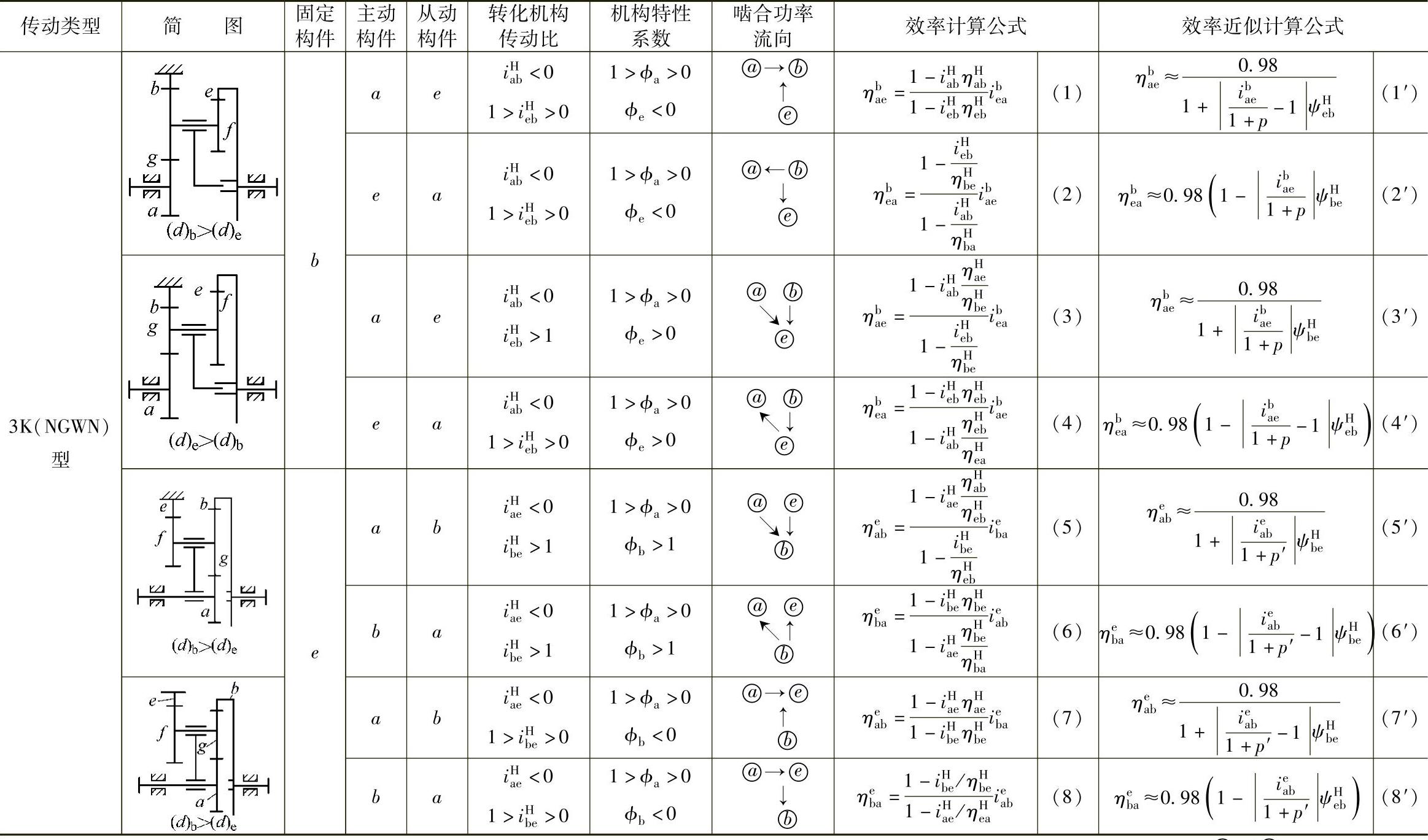
注：表中p=z_b/z_a，p′=z_gz_e/z_az_f，ψ^H=1-η^H，ϕ_a=N_b^H/N_a，ϕ_b=N^H_b/N_b，ϕ_e=N^H_e/N_e，ψ^H_be=ψ^H_gb+ψ_f^He。→表示啮合功率流向。例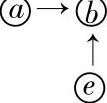表示啮合功率由构件a、e输入，并列流向构件b输出。（d）b、（d）e表示齿轮b和e的分度圆直径。

表9-7 特殊3K（NGWN）型行星传动的效率计算式

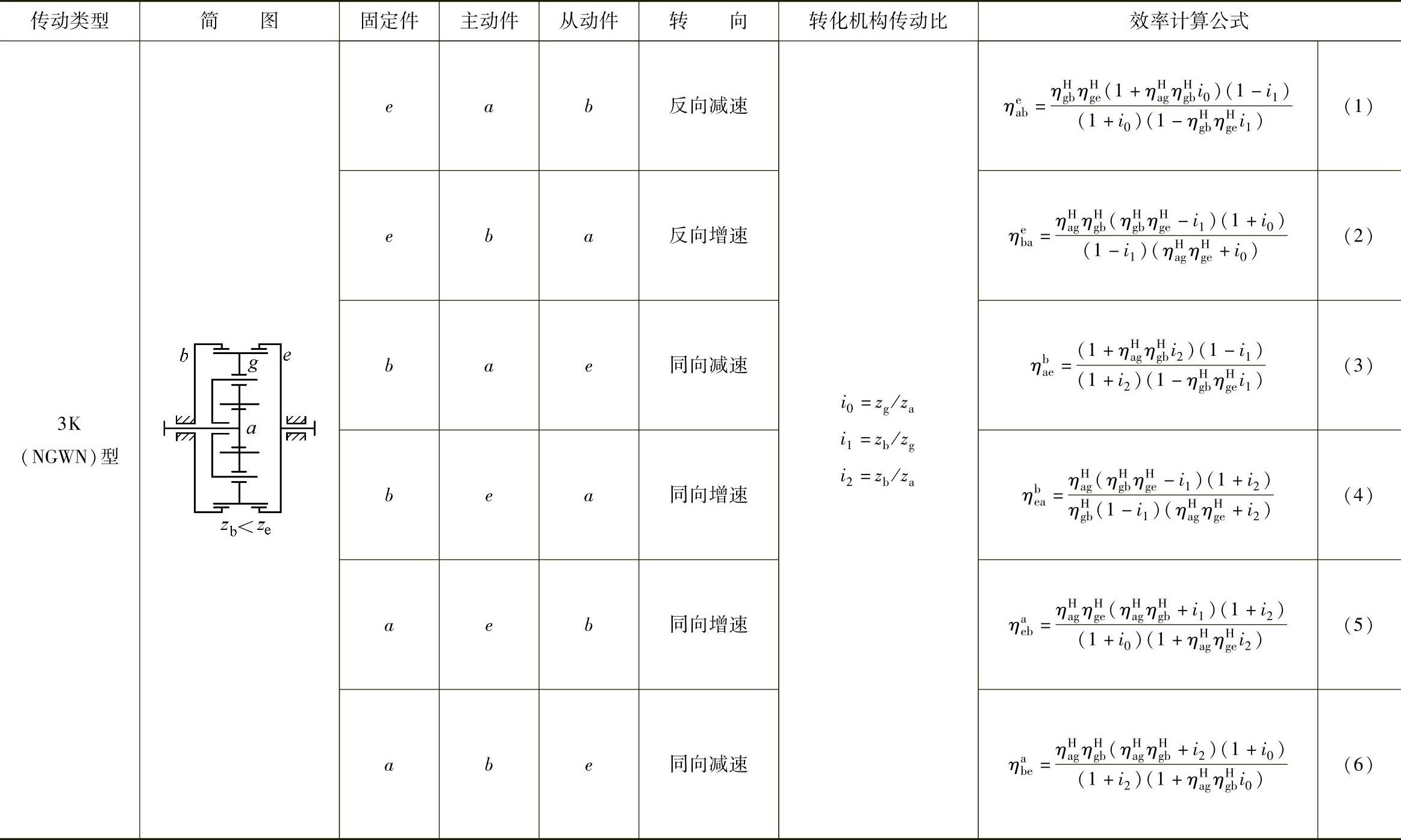
注：η_a^H-g、η^H_g-b、η^Hg-e为转化机构各对齿轮啮合的效率。在计算传动效率时，理应考虑轴承效率，但因该种传动通常均用滚动轴承，其损失较啮合损失小得多，将其忽略对效率影响不大。