图9-1所示为最常用的3K型行星轮系，它由高速级2K-H（NGW）型和低速级2K-H（NN）型组成。所以，3K型行星轮系的配齿数可转化为两级串联的2K-H型行星轮系的配齿数问题，即可应用前面介绍的2K-H型配齿方法。由于3K型是由两个2K-H型串联组成的，所以3K型配齿数时，除将两级分别满足传动比、同心、邻接和装配四个约束条件进行配齿外，尚需考虑两级间的联系问题，如两级传动比如何分配；两级之间因有公用的齿轮副，需要满足共同的同心条件等。所以，3K型行星轮系配齿数时要稍复杂一些。

通常取z_a、z_b、z_e为行星轮个数n_p的整数倍，而且各齿轮的模数均相等。在3K型传动中，除要求输入轴和输出轴回转方向相反而采用z_b＜z_e外，一般推荐用z_b＞z_e。在同样条件下，后者比前者的承载能力大，且i^b_ae≤100时，齿轮圆周速度和行星架转速均略有降低。

在最大齿数相同的条件下，当z_g=_f时，能获得较大的传动比，且制造方便，减少装配误差，使各行星轮之间载荷分配均匀。此外，相啮合的齿轮齿数间没有公因数的可能性比z_g≠z_f时为小，因而提高了传动的平稳性。但存在变位困难（尤其是n_p较大时）的缺点，计算所得的齿数是否好用，通常在变位计算后才能确定。

3K型配齿数时，首先应先解决传动比分配问题，然后才能对两级2K-H型分别进行配齿数。分配传动比主要应满足两级之间共同的同心条件（即两级之间的主要联系）来进行。下面按由NGW型和NN型串联组成的、最常用的3K型进行分析，介绍其配齿数的方法。

高速级2K-H（NGW）型的齿数和为

低速级2K-H（NN）型的齿数和为

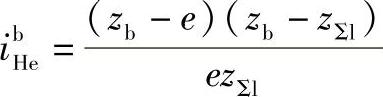
移项得

该两级应满足共同的同心条件为

又因

由式（9-4）、式（9-5）解得

当给定3K型传动比i^b_ae，选取z_b和e后，可按式（9-4）、式（9-5）分配其传动比。

关于如何选取z_b和e值，通过理论分析和配齿实践可以看到。

设先给定z_b，随着i^b_ae的增大，z_a就趋于减少。当选取e值偏大，也会导致z_a减少，所以在传动比偏大时，应取偏小的e值，以免z_a过小而造成根切。

设先给定z_a，随着i^b_ae的增大，z_b就趋于增多。当选取e值偏大，也会导致z_b增多，所以在传动比偏大时，应取较小的e值，以免z_b过大而使轮廓尺寸增大。

通过理论分析和实践经验，推荐表9-2，供3K型配齿数时选取e值和z_b值参考用。

表9-2 3K型行星齿轮传动配齿数时的e、z_b值选取

由于3K型行星轮系的传动比较大，为了能满足邻接条件，一般取行星轮个数n_p=3。

为了方便配齿数，易于满足装配条件，故配齿时一般都取中心轮齿数及e值为n_p=3的倍数。

下面就这种简便的配齿数方法，列出其配齿数的步骤及配齿公式。

根据传动比i^b_ae的大小，查表9-2选取合适的z_b值及e值。若传动比i^b_ae为负值时，取e为负值。

分配传动比

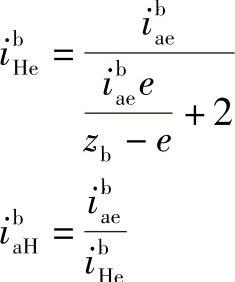
计算各轮齿数

装配条件要求z_a值应为n_p=3的倍数，如果非角度变位，还要求z_a应与z_b同为奇数或偶数，以满足同心条件。角度变位则无此要求。如果计算的z_a值没有满足上述要求，则应重新选取z_b或e值进行计算。

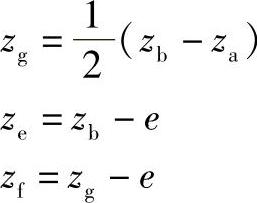
验算传动比

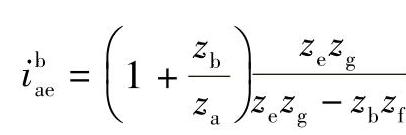
必要时验算邻接条件，根据i^b_aH及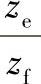比值查表8-4校核邻接条件。

例9-2 已知3K型行星轮系，i^b_ae=200，n_p=3，试配齿数。

解 1）由i^b_ae=200，查表9-2，选取z_b=105，e=3。

2）分配传动比

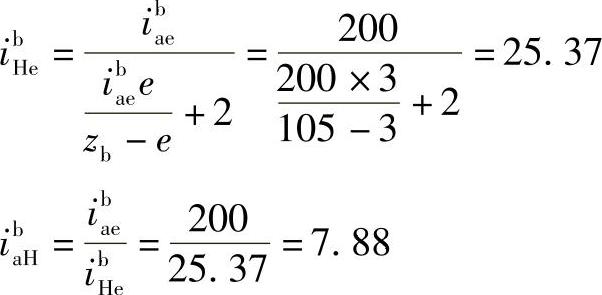
3）计算各齿轮齿数

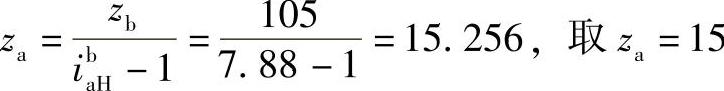
z_a=15既是n_p=3的倍数，又与z_b^一样同为奇数。

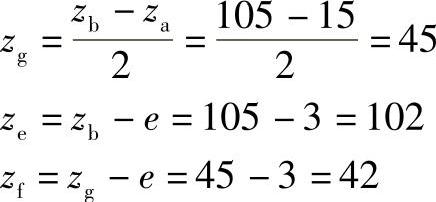
4）验算传动比

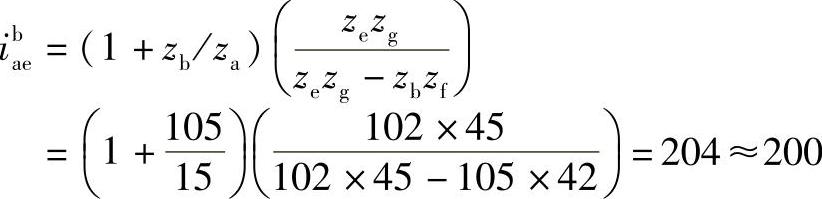
5）检验邻接条件

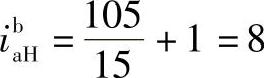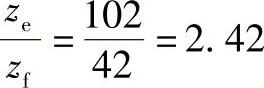由及，查表8-4满足邻接条件。

结果：z_a=15，z_b=105，z_e=102，z_g=45，z_f=42，i^b_ae=204。

例9-3 已知3K型行星轮系i^b_ae=-32，n_p=3，试配齿数。

解 1）由i^b_ae=-32，查表9-2选取z_b=96，e=-12。

2）分配传动比(www.daowen.com)

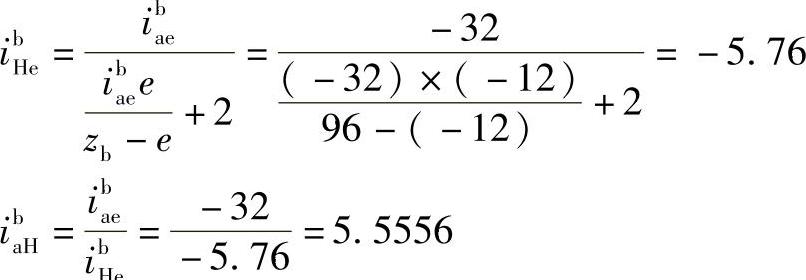
3）计算各轮齿数

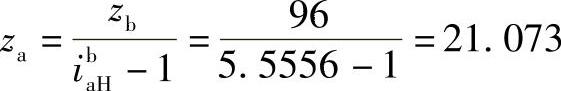
取z_a=21（为n_p=3的倍数），

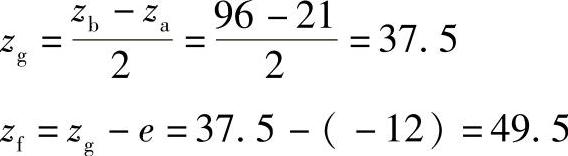
取z_g=37，z_f=49（同时减半个齿，然后用角度变位来满足同心条件），

z_e=z_b-e=96-（-12）=108

4）验算传动比

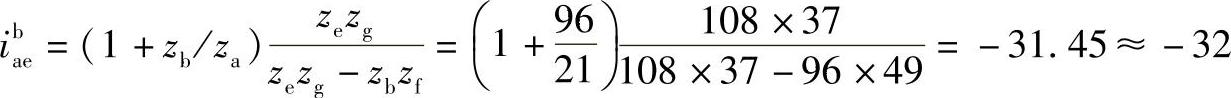
5）检验邻接条件

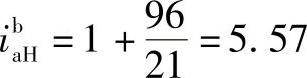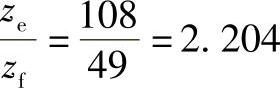根据及，查表8-4满足邻接条件。

结果：z_a=21，z_b=96，z_e=108，z_g=37，z_f=49，i^b_ae=-31.45

在3K型行星齿轮传动中，可使行星轮齿数z_f=z_g，这时可采用角度变位来保证同心条件，α_a′_g=α_g′_b=α_f′_e，以致可大大简化行星轮的加工工艺，无需对齿槽，也不必为了轮齿的滚切和磨削而采用分开式的行星轮结构。由于消除了行星轮齿圈z_f和z_g的角度位置误差，故可提高齿轮传动的精度。但是单齿圈行星轮的3K型传动，当不能避免使变位系数和很大（xΣ>1）时，由于啮合线的工作区偏离节点和滑动速度增大，其效率将略有降低。

当行星轮齿数z_f=z_g时，其传动比为

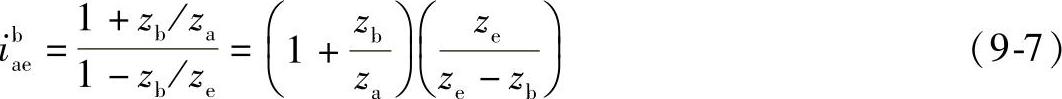
据各行星轮能均匀装入中心轮a、b和e之间的要求，即应满足如下的装配条件：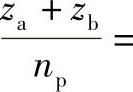

z整数和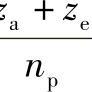=整数（9-8）

式中 n_p——行星轮个数，一般取n_p=3。

由式（9-7）可知，欲使3K型传动的传动比i^b_ae增大，使结构紧凑，就应尽量减小z_e与z_b的差值。但从满足装配条件来看，它们的最小差值应为

z_e-z_b=n_p （9-9）

将式（9-9）代入式（9-7），则得

z²_e+ze（z_a-n_p）-i^b_aez_an_p=0

所以

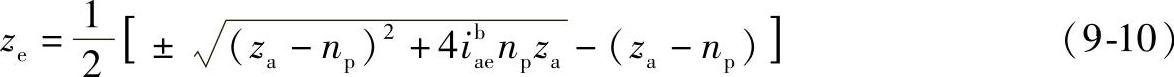
且有

z_b=z_e-n_p

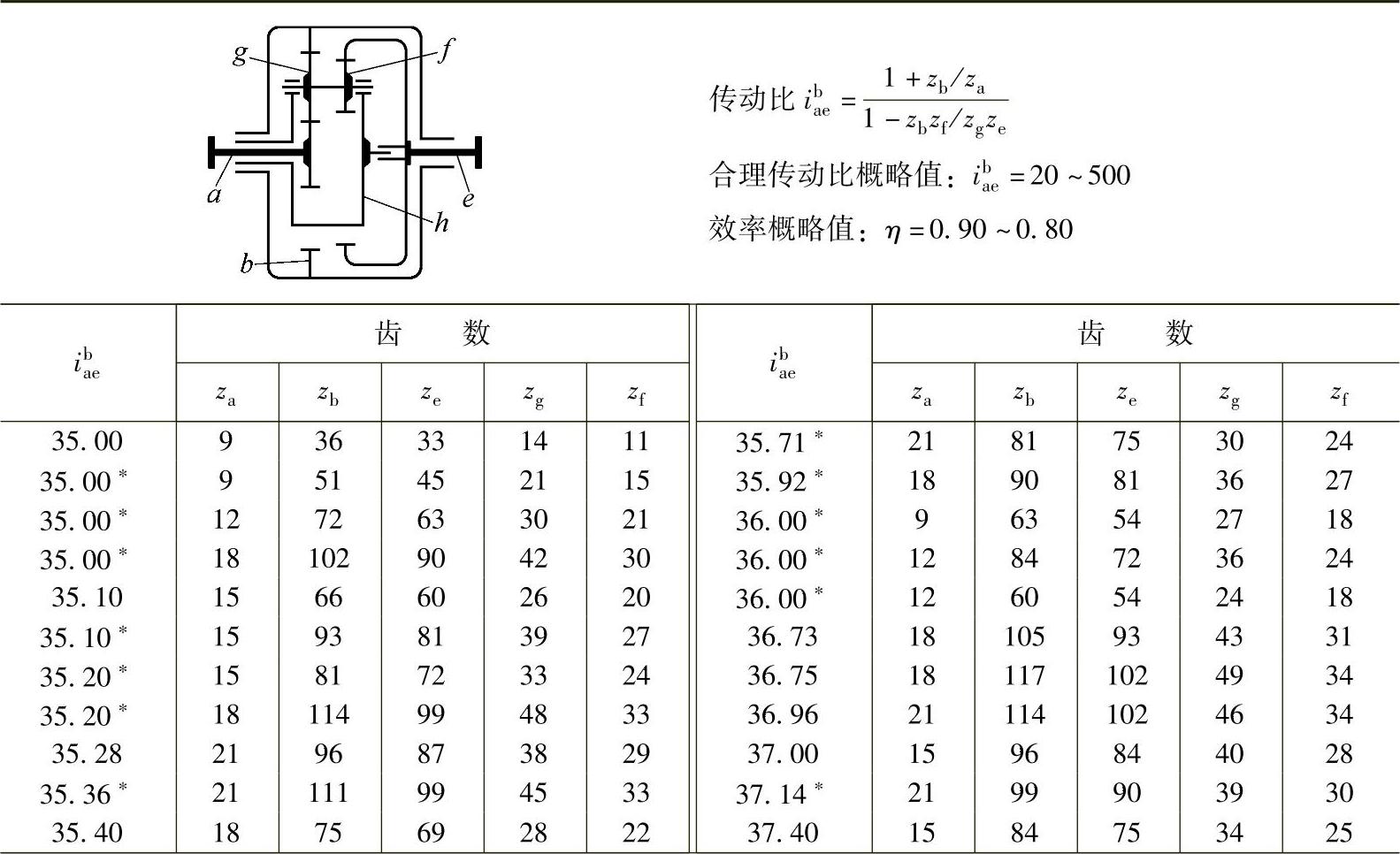
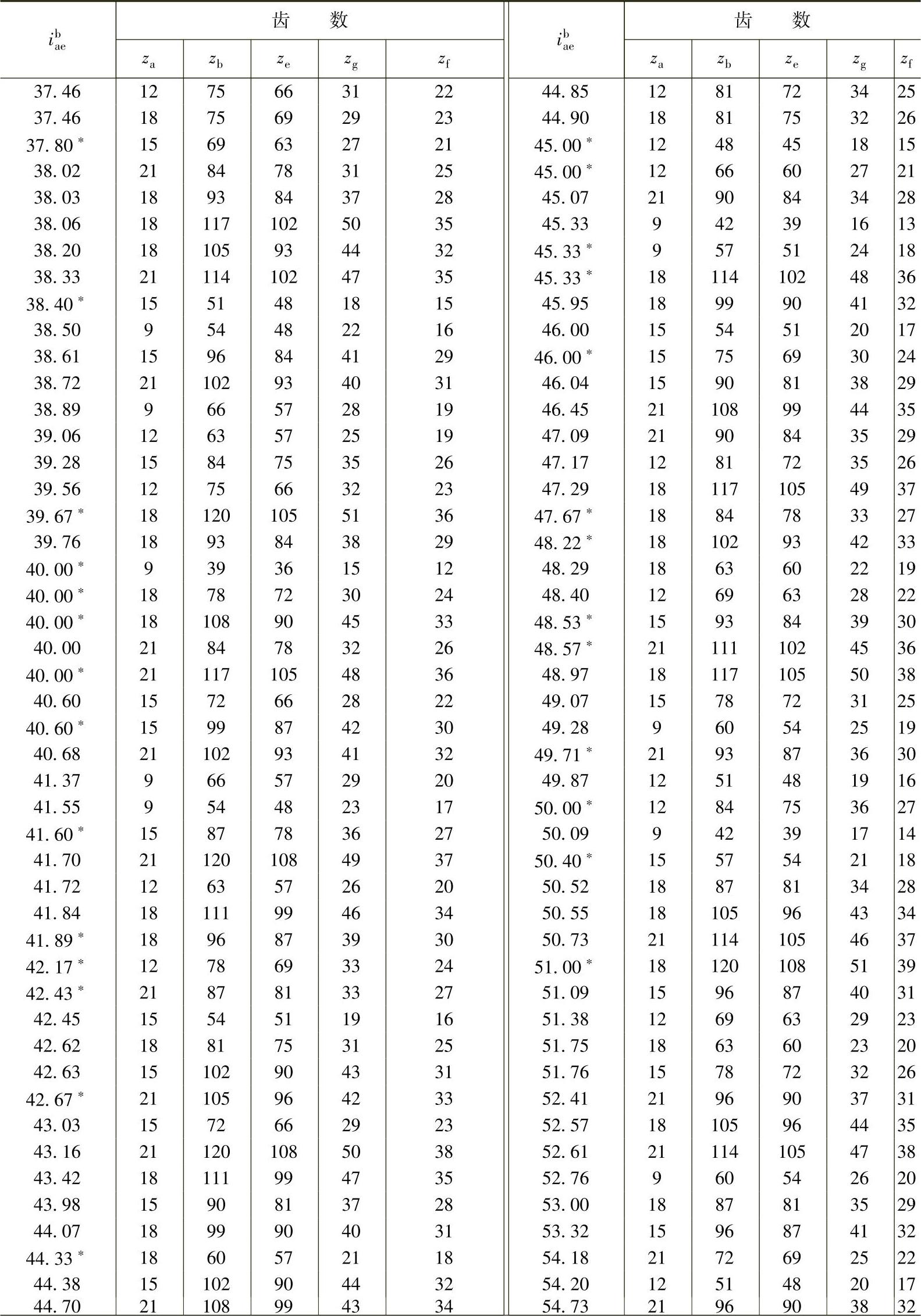
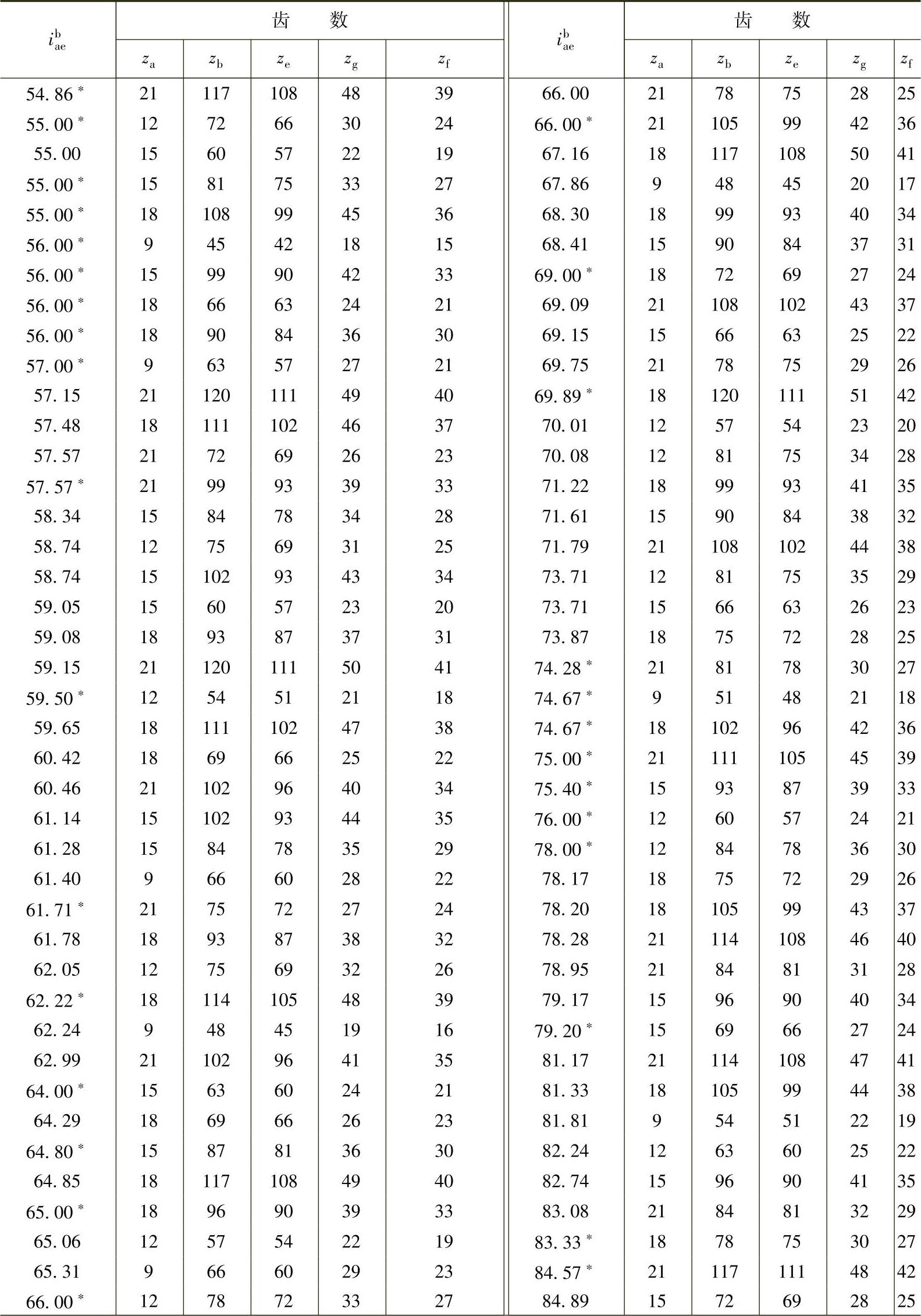
内齿圈b固定时，按传动比i^b_ae确定3K型行星传动的齿数，见表9-3。

按传动比i^b_ae确定单齿圈行星轮的3K型行星传动的齿数，见表9-4。

表9-3 内齿圈b固定时，按传动比i^b_ae确定3K型行星传动的齿数

（续）

（续）

（续）

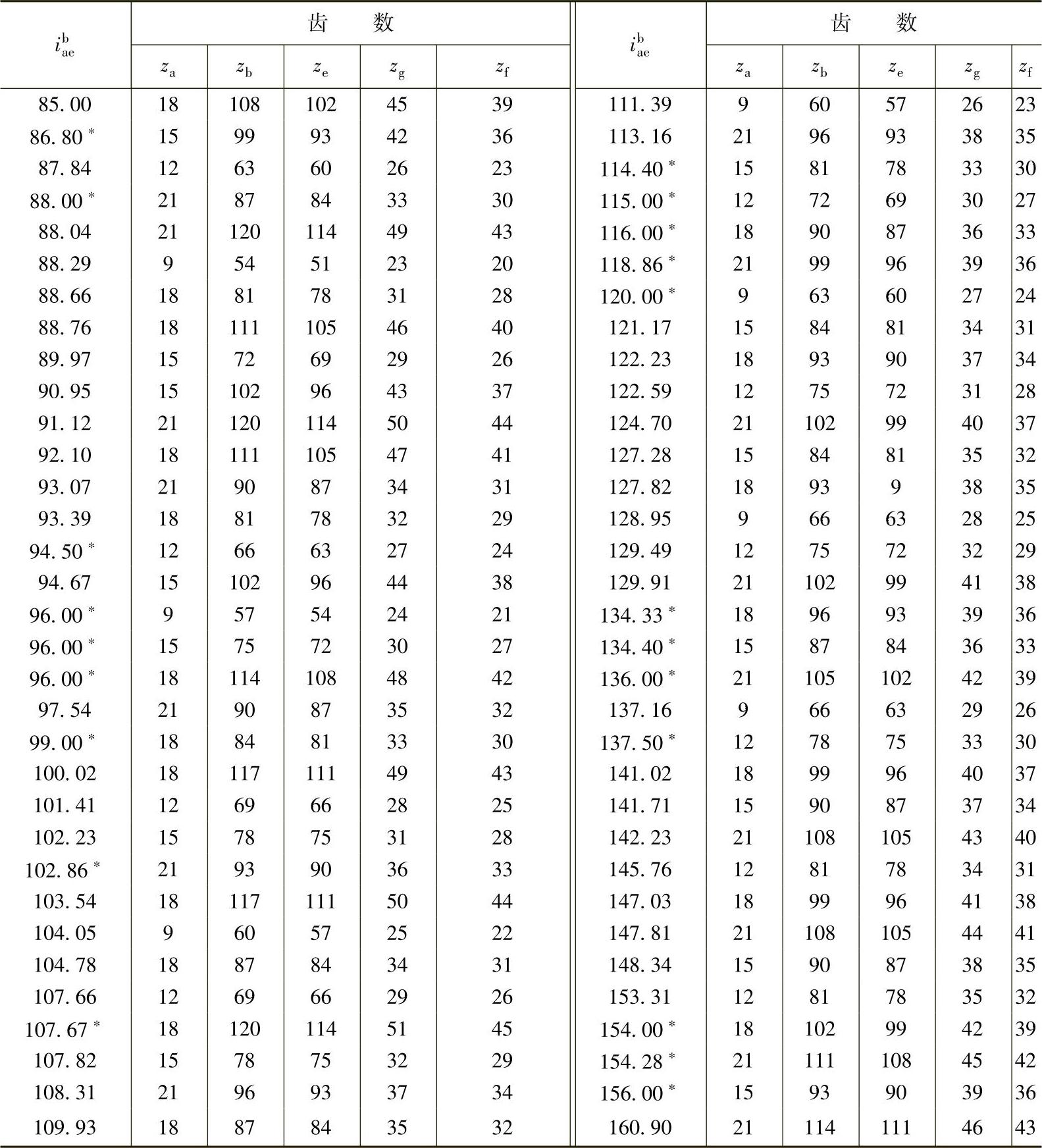
注：1.本表所有齿轮的模数均相同，m_ta=m_tb=m_te。

2.标有星号的传动中z_a+z_g=z_b-z_g=z_e-z_f，因此（α_t′）a=（α_t′）b=（α_t′）e和x_a+x_g=x_b-x_g=x_e-x_f。

3.在所有情况下，z_a、z_b和z_e都是3的倍数（在某些情况下也是2的倍数），因此本表可用于行星轮数具有n_p=3的传动（有时n_p=2亦适用）。

4.在所有情况下，z_b-z_g=z_e-z_f，因此，（α_t′）b=（α_t′）e，x_b-x_g=x_e-x_f。

5.在所有情况下，z_b＞z_e，z_g＞z_f，z_g＞z_a。

6.表中i^b_ae值只有正的，因此，中心轮a和e的旋转方向相同。

7.表中i^b_ae值精确到小数点后第二位，当传动需要更准确的传动比数值时，应按表中3K传动的公式确定。

表9-4 按传动比i^b_ae确定单齿圈行星轮的3K型行星传动的齿数（n_p=3）

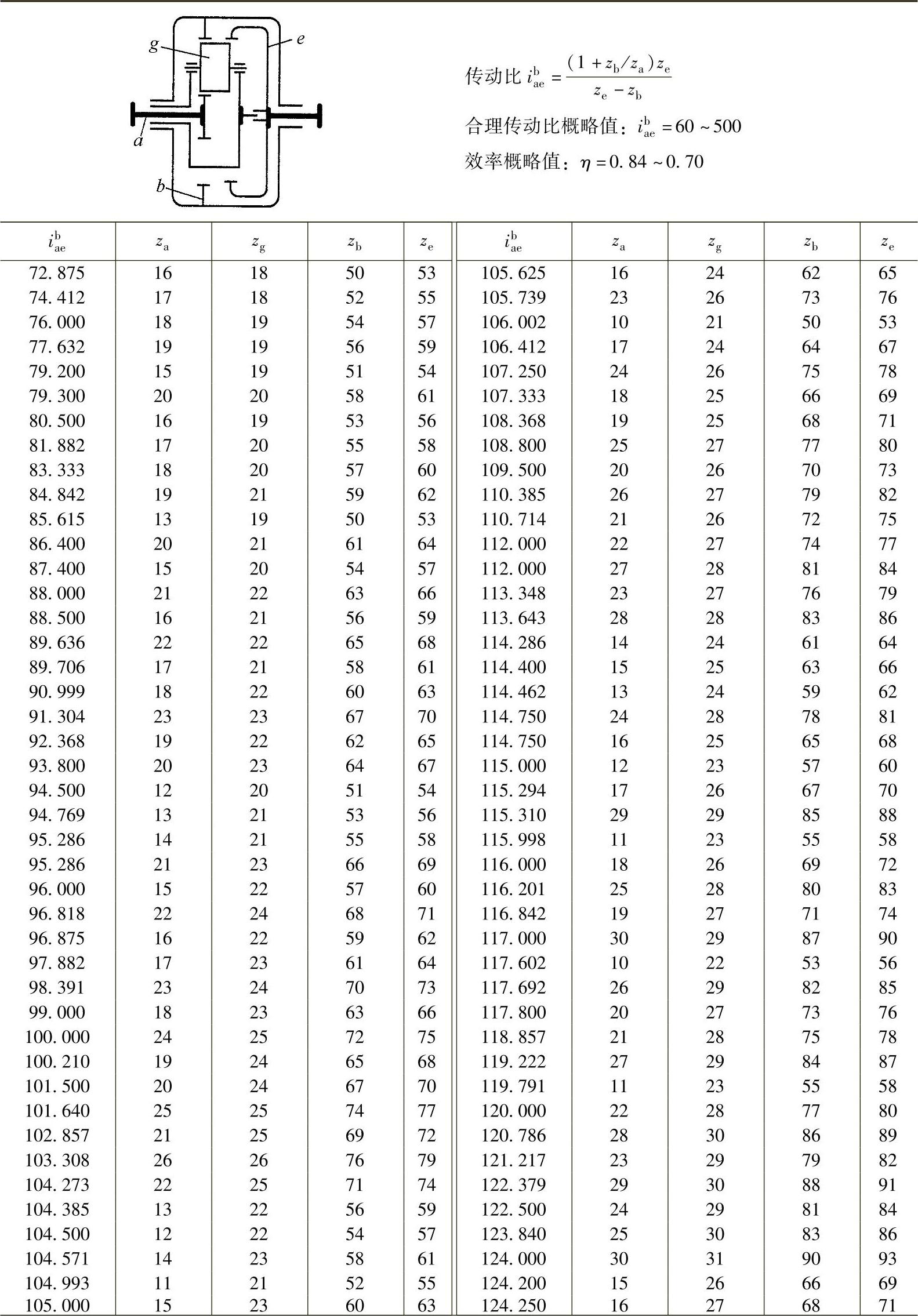
（续）

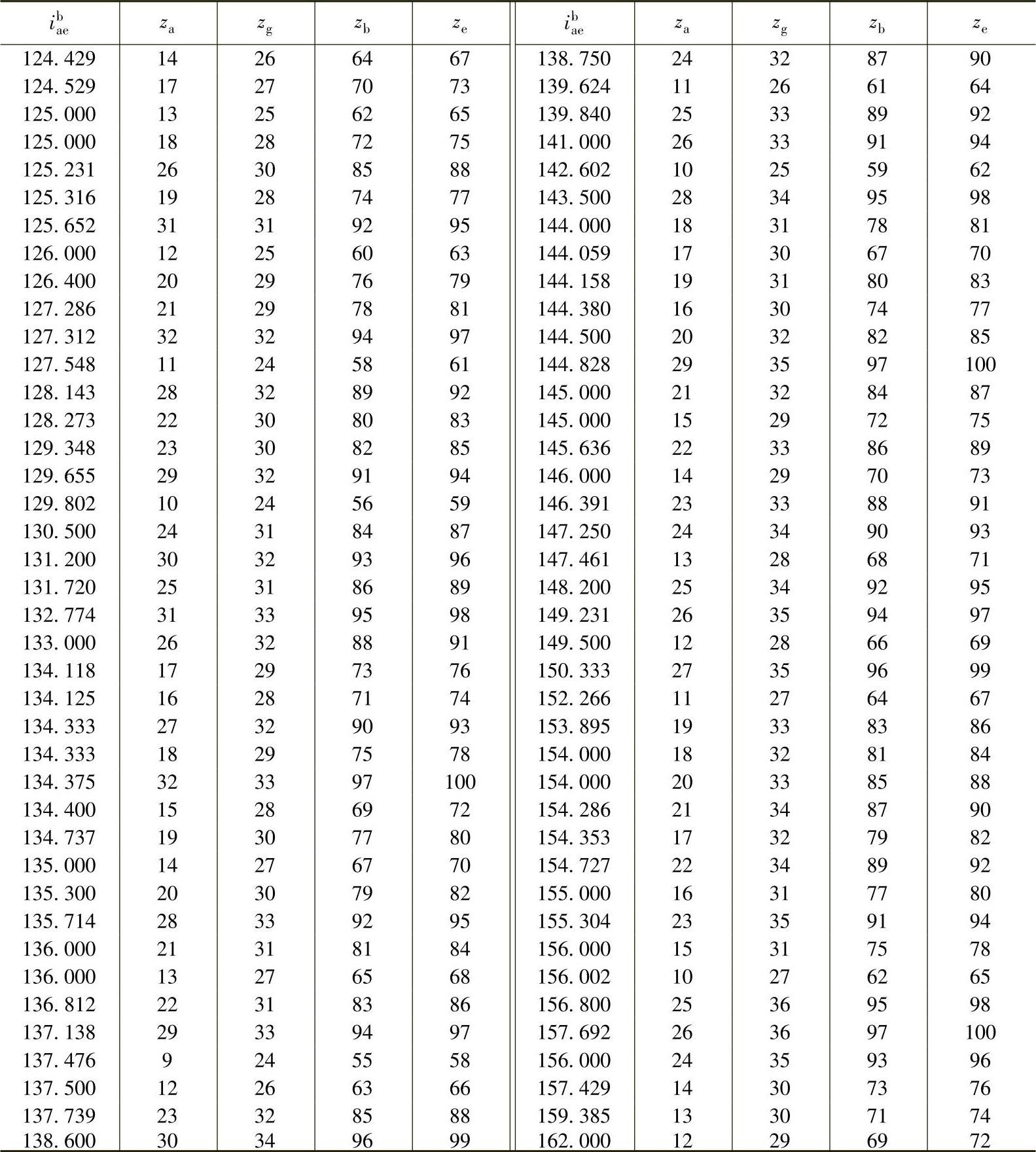
注：1.本表采用齿数z_g≥z_a的数据。但列入数据由条件z_g≥z_a进行限制，以提高由啮合强度和轴承的工作能力所限制的承载能力。

2.传动比按下式确定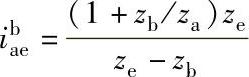

值i^b_ae为正，因此，中心轮a和e的转动方向相同。

3.需要得到传动比小于零的传动时，用固定中心轮e来实现。这时i^e_ab=1-i^b_ae或i^e_ab=i^b_ae-1。因此，从表中选择齿数时，是用近似于i^b_ae而比i^e_ab大1的值来确定的。例如，已知i^e_ab=-115，则用表中的i^b_ae=116齿数来确定。