探讨行星齿轮传动效率公式的普适性

图8-84所示为一行星差动轮系，a、b和H是三个外伸轴，将其中一轴（如b或H）固定，便得到一行星轮系或定轴轮系。另外两轴间的传动效率可用如下公式表示：

（1）b固定时

当a主动时，轮系的效率为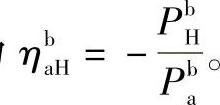

当a从动时，轮系的效率为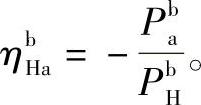

图8-84 行星差动轮系

式中，P^b_a、P^b_H分别为a轴和H轴在b轴固定时传递的功率。上面两式可统一表示为

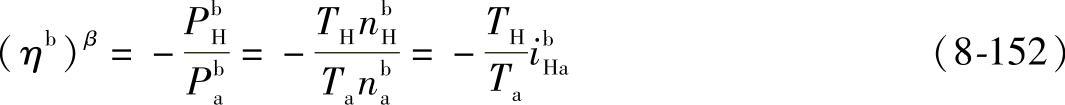
式中 β——当a主动时，β=+1，当a从动时，β=-1；

T_a、T_H——a、H轴传递的转矩；

n^b_a、n^b_H——b固定时，a、H的转速；i^b_Ha——b固定时，H、a间的传动比，或当b未作固定时，对b作相对运动时H、a间的传动比。同理i^a_Hb为a固定或对a作相对运动时H、b间的传动比。i^b_Ha与i^a_Hb的关系为i^b_Ha=1-i^a_Hb。

（2）H固定时

当a主动时，轮系的效率为。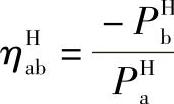

当a从动时，轮系的效率为η_b^Ha=-P^H_a/P_b^H。

式中，P^H_a、P^H_b分别为a轴和b轴在H轴固定时传递的功率。上面两式可统一表示为

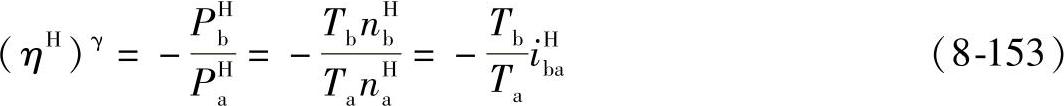
式中 γ——当a主动时，γ=+1，当a从动时，γ=-1；

T_b——b轴传递的转矩；(https://www.daowen.com)

n^H_a、n_b^H——H固定也即对H作相对运动时a、b的转速；

i^H_ba——H固定或对H作相对运动时b、a间的传动比。

此外，根据轮系受力的平衡条件，其三个外伸轴a、b和H传递的转矩必须满足

T_a+T_b+T_H=0 （8-154）

联立解式（8-152）、式（8-153）和式（8-154）可得

（η^b）β=1-i^a_Hb[1-（η^H）γ]

因为β=±1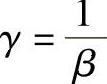，，所以

η^b={1-i^a_Hb[1-（η^H）γ]}^β （8-155）

这里，b一般可作为实际行星轮系的固定件，而H为其转化机构的固定件。当b固定、a主动时，β=+1，a从动时，β=-1；当H固定、a主动时，γ=+1，a从动时，γ=-1。

式（8-155）表达了当b、H分别固定时，得到的两轮系的效率η^b与η^H间的关系普遍式。式中β的正、负根据实际轮系a是否主动来判定（即按啮合功率流的方向来判定），但γ的正、负要根据转化机构中a是否主动来定。必须指出：一个轮系加上一个公共转速而改变了固定件时，原来的主动件不一定还是主动。因为

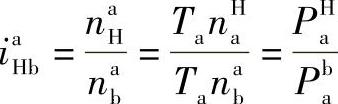
若i^a_Hb＞0时，则P^H_a与P^b_a符号相同，说明改变固定件（由b→H）时，a不变其主、从关系。

若i^a_Hb＜0时，则P^H_a与P^b_a符号相反，说明改变固定件（由b→H）时，a改变了其主、从关系。因此，根据i^a_Hb的正、负可判定γ的正、负。它共有四种可能：

b固定时a主动，而i^a_Hb>0，则H固定时a仍为主动，此时β=+1，γ=+1。

b固定时a主动，而i^a_Hb<0，则H固定时a变为从动，此时β=+1，γ=-1。

b固定时a从动，而i^a_Hb>0，则H固定时a仍为从动，此时β=-1，γ=-1。

b固定时a从动，而i^a_Hb<0，则H固定时a变主动，此时β=-1，γ=+1。