齿轮传动中的功率损失，包含啮合摩擦损失、轴承摩擦损失、润滑油的飞溅和搅拌损失。因此，传动效率可按下式确定：

η=η_mη_Bη_s

式中 η_m、η_B、η_s——考虑啮合损失、轴承摩擦损失、润滑油飞溅和搅拌损失时的效率。

因为_η值接近于1（通常η>0.95），所以上式可改写成如下形式：而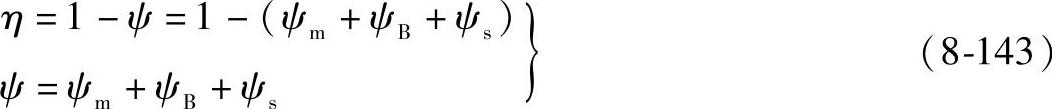

式中 ψ——传动损失系数；

ψ_m=1-η_m，ψ_B=1-η_B，ψ_s=1-η_s

ψ_m、ψ_B、ψ_s——啮合、轴承摩擦、润滑油飞溅和搅拌损失系数。

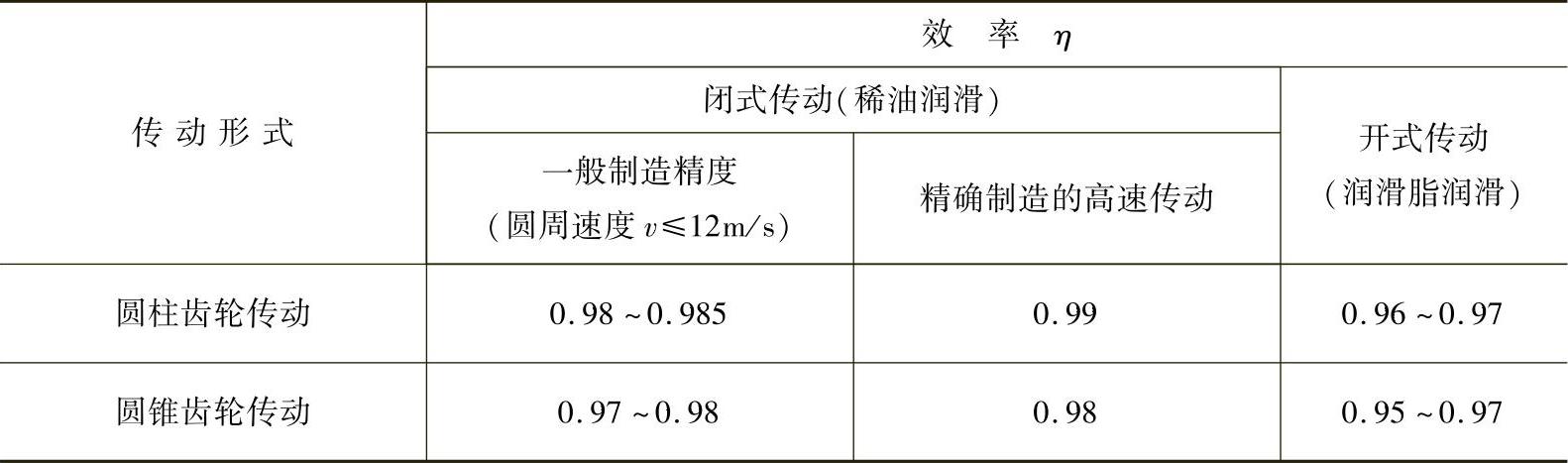
表8-28中，给出了支承为滚动轴承的单级齿轮传动效率的概略值。滚动轴承支承的通用两级圆柱齿轮减速器，当齿轮为油浴润滑时，其效率_η=0.97。多级齿轮传动的效率概略值，可按表8-28推荐的资料得出。

表8-28 滚动轴承支承的单级齿轮传动效率概略值

（1）基本啮合效率η_m的计算（包括ψ_m值的确定）

行星齿轮传动的效率是以轴线不动时一对齿轮的啮合效率为基础进行计算的，称之为基本啮合效率，用符号η_m表示。在设计时为了对几个方案进行比较，评定效率的高低或检验是否自锁，通常只根据啮合损失计算效率。这样计算的效率对高速行星齿轮传动，其误差往往较大，而对于低速的行星齿轮传动与实际情况比较符合。所以，如何精确地计算_ηm是相当重要的。

下面介绍几个常用的公式：

1）前苏联学者库德略夫采夫（В.Н.Кудрявцев）公式

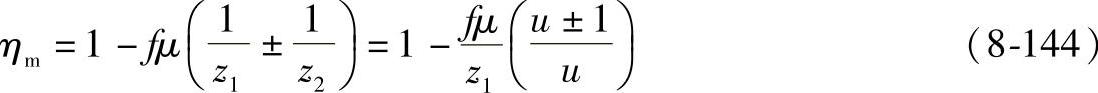
式中 u=z2/z1，“+”号用于外啮合，“-”号用于内啮合；

μ——摩擦因数，通常取μ=0.06～0.100；

f——与两齿轮齿顶高系数h_a*有关的系数，h_a*≤m时，f=2.3，h_a*=（1～1.8）m时，f=3.1。

2）英国学者塔普林（Tuplin）公式

此式用于有效齿高为2m、摩擦因数μ=0.05的场合，其余符号意义同上。

3）德国学者克莱因（Klein）公式

此式用于摩擦因数_μ=0.03～0.05，即工作及润滑良好的情况下，其余符号意义同上。

4）日本学者两角宗晴公式

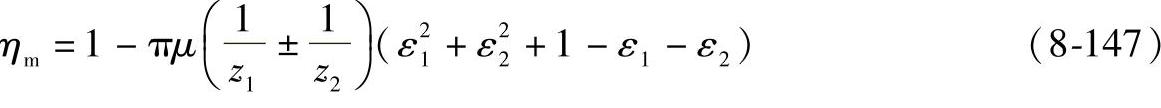
此式在重合度1<ε_α<2时使用，式中摩擦因数_μ假定在啮合中为一定值。其余符号意义同上。

ε₁=g₁/p_b

ε₂=g₂/p_b

ε_a=ε₁+ε₂

式中 g₁——节点p至啮合终点B₁的距离；

g₂——啮合起点B₂至节点的距离；

p_b——基节。

以上四种公式中，两角宗晴的公式最精确。两角宗晴的公式经过简化，可以得到其他三种方法的公式。我国广大工程技术人员用前苏联库德略夫采夫公式的居多。现以库德略夫采夫公式为例，讨论ψ_m、ψ_B、ψ_s值的确定。

啮合损失系数ψ_m的确定：

对于非变位和高度变位的直齿轮、斜齿轮传动的ψ_m值，按下式计算，其误差不大。

式中 u=z2/z1，“+”号用于外啮合，“-”号用于内啮合；

K_ψ——根据x=|x₁|=|x₂|，由图8-82所示的曲线确定；

μ——摩擦因数的平均值，根据vΣ=2υsinα_t′，按图8-83所示的曲线确定，α_t′为端面啮合角。

式（8-148）也可近似地用于角度变位及非标准基准齿形的齿轮传动中。对于β=0和ε_α＜2的传动，可按下列方法以足够的精度确定ψ_m值。ε₁、ε₂与ε_α值的计算公式为

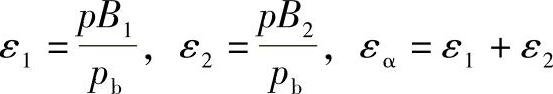(www.daowen.com)

与一般计算重合度公式相同。

若ε₁与ε₂均小于1，则

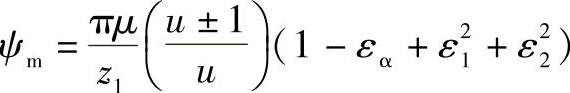
当ε₁＞1时，则

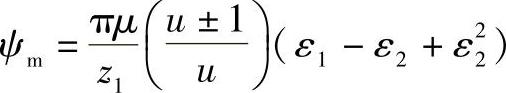
当ε₂＞1时，则

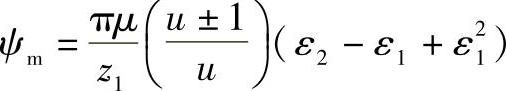
（2）轴承损失系数ψ_B的确定ψ_B可按下式确定

式中 T_fi——第i只轴承的摩擦力矩；

n_i——第i只轴承的转速（r/min）；

T₂、n₂——从动轴上的转矩、转速。

对行星轮轴承式（8-149）中的转速n_i为行星轮相对于行星架的转速。

滚动轴承的摩擦力矩T_f（N·mm），可近似地按下式确定：

T_f=5pdμ₀

式中 d——安装滚动轴承的轴颈直径（mm）；

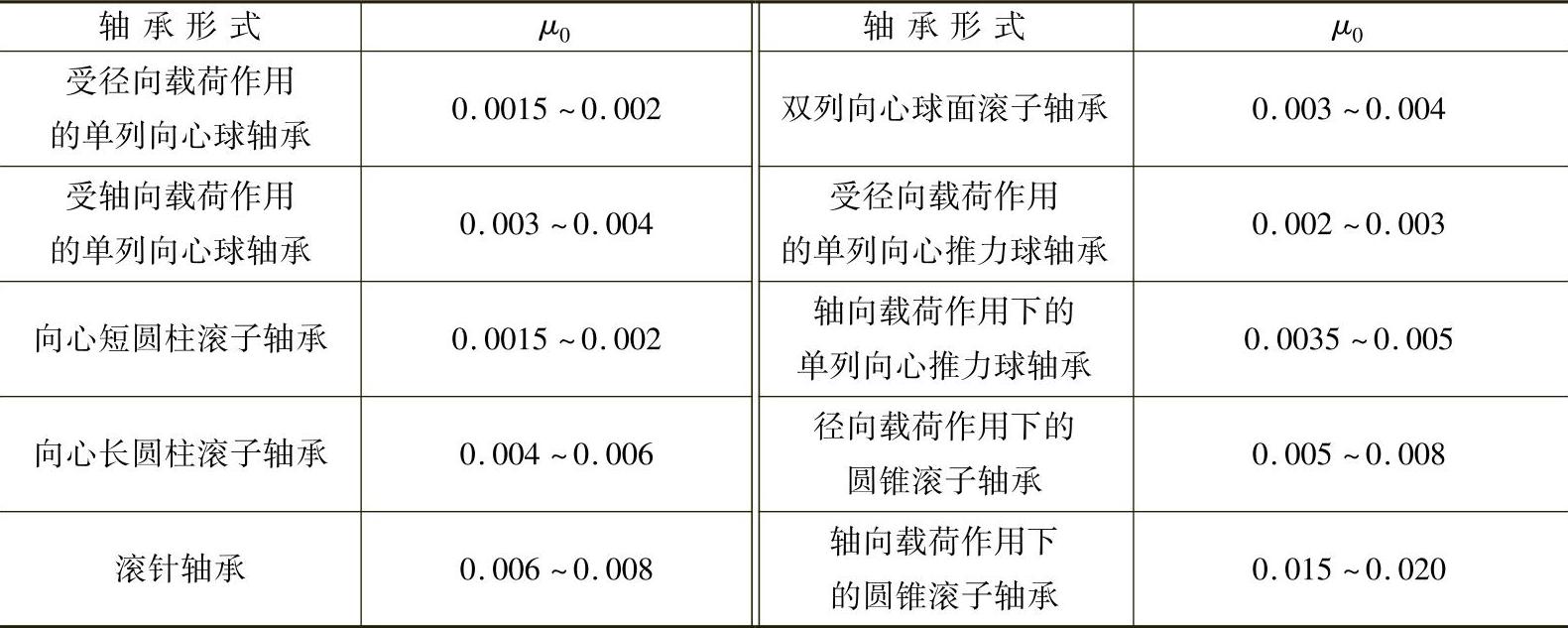
μ₀——当量摩擦因数，见表8-29；

p——滚动轴承上的载荷（N）。

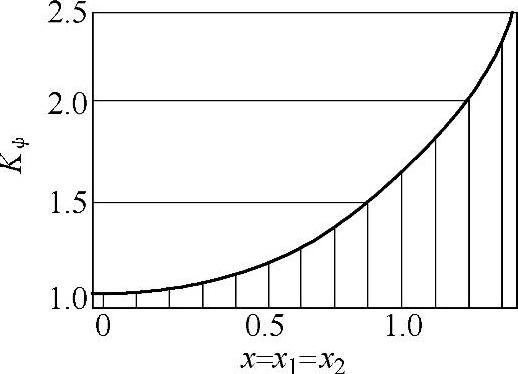
图8-82 Kψ值的计算曲线

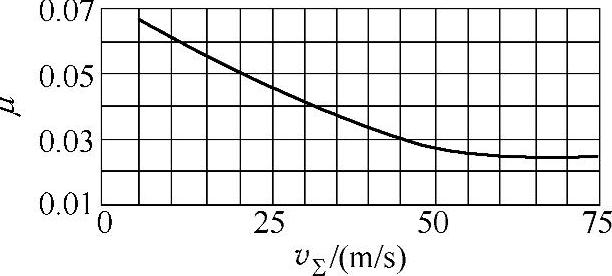
图8-83 随vΣ变化的接触中的摩擦因数

对照总的损失来看，在滚动轴承中的损失只占很小一部分。但是，滚动轴承中的损失所占比例很大的情况也是存在的，例如，双内啮合2K-H（NN）型少齿差行星齿轮传动，其滚动轴承的损失大大超过啮合损失。

表8-29 滚动轴承当量摩擦因数μ0

通常在设计时，轴承的传动效率可直接由有关设计手册查得。

（3）油阻损失系数ψ_s的确定

当齿轮浸入润滑油的深度为（2～3）m（m为模数）时，考虑油阻损失系数可近似由下式确定：

式中 v——齿轮圆周速度（m/s）；

b——浸入润滑油的齿轮宽度（cm）；

P——传递功率（kW）；

ν——润滑油在工作温度时的运动粘度（cSt，1cSt=10^-6m²/s）；

zΣ——齿数和。

在喷油润滑条件下，ψ_s值可按式（8-150）求得的ψ_s值乘以0.7选取。

如果载荷是周期性变化的，并且在这周期性变化的作用时间内，减速器的温度变化可忽略不计，则式（8-150）中的功率P，应按时间的平均值代入，其值可按下式确定：

式中 P_i——在时间i内的功率值；

t_i——功率变化周期的持续时间。

在行星齿轮传动中，为了便于实际计算，在传动效率的表达式中，用固定行星架H时的效率_η^H和传动损失系数ψ^H来表示，其上、下标的标记方法、意义和传动比的标法相同，如ψ^H=1_-η^H，为行星架H固定时的传动损失系数。